
- •22 Кафедра математического анализа
- •Глава 1. Дифференциальные уравнения
- •§1 Дифференциальные уравнения первого порядка
- •Уравнение вида
- •§2. Дифференциальные уравнения высших порядков. Основные понятия
- •§3. Уравнения второго порядка, допускающие понижение порядка
- •§4. Линейные однородные дифференциальные уравнения второго порядка
- •§ 5. Линейные неоднородные дифференциальные уравнения второго порядка
- •§6. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •§7. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Задания для самостоятельного решения
§6. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Рассмотрим линейное однородное уравнение второго порядка
|
(30) |
где
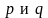 - вещественные числа.
- вещественные числа.
Теорема
1.
1) Если число
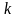 - вещественный корень уравнения
- вещественный корень уравнения
|
(31) |
то
функция
 является решением уравнения (30).
является решением уравнения (30).
2)
если числа
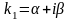 и
и
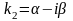 (
(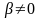 )
– комплексные корни уравнения (31), то
функции
)
– комплексные корни уравнения (31), то
функции
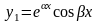 и
и
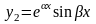 являются решениями уравнения (30).
являются решениями уравнения (30).
Уравнение (31) называется характеристическим уравнением данного уравнения (30).
Характеристическое
уравнение (31) является квадратным
уравнением и, следовательно, имеет два
корня. Обозначим их
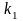 и
и
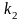 .
.
Теорема
2.
1) Если корни характеристического
уравнения вещественные и различные
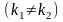 ,
то общее решение уравнения (30) имеет вид
,
то общее решение уравнения (30) имеет вид
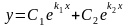 ;
;
2)
если корни характеристического уравнения
вещественные и равные
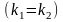 ,
то общее решение имеет вид
,
то общее решение имеет вид
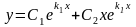 ;
;
3)
если корни характеристического уравнения
комплексные
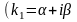 ,
,
,
,
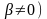 ,
то общее решение имеет вид
,
то общее решение имеет вид
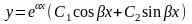 .
.
Пример
1.
Найти общее решение уравнения
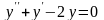 .
.
Характеристическое
уравнение имеет вид
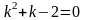 ;
его корни
;
его корни
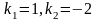 вещественные и различные. Соответствующие
частные решения уравнения
вещественные и различные. Соответствующие
частные решения уравнения
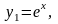
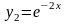 .
Общее решение уравнения имеет вид
.
Общее решение уравнения имеет вид
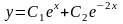 .
.
Пример
2.
Найти общее решение уравнения
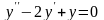 .
.
Характеристическое
уравнение имеет вид
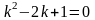 ;
его корни
;
его корни
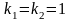 вещественные и равные. Соответствующие
частные решения уравнения
вещественные и равные. Соответствующие
частные решения уравнения
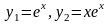 .
Общее решение уравнения имеет вид
.
Общее решение уравнения имеет вид
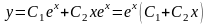 .
.
Пример
3.
Найти общее решение уравнения
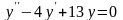 .
.
Характеристическое
уравнение имеет вид
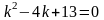 ;
его корни
;
его корни
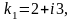
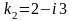 комплексные. Соответствующие частные
решения уравнения
комплексные. Соответствующие частные
решения уравнения
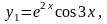
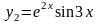 .
Общее решение уравнения имеет вид
.
Общее решение уравнения имеет вид
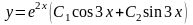 .
.
Контрольные вопросы:
Какой вид имеет общее решение линейного однородного уравнения второго порядка с постоянными коэффициентами в случае действительных различных корней характеристического уравнения?
Какой вид имеет общее решение линейного однородного уравнения второго порядка с постоянными коэффициентами в случае равных корней характеристического уравнения?
Какой вид имеет общее решение линейного однородного уравнения второго порядка с постоянными коэффициентами в случае комплексных корней характеристического уравнения?
§7. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
Рассмотрим неоднородное линейное уравнение второго порядка
|
(32) |
где
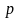 и
и
 - вещественные числа;
- непрерывная функция.
- вещественные числа;
- непрерывная функция.
Общее
решение такого уравнения представляет
собой сумму частного решения неоднородного
уравнения и общего решения соответствующего
однородного уравнения. Так как общее
решение однородного уравнения мы
находить умеем, поэтому остается
рассмотреть вопрос о нахождении частного
решения. Для нахождения частного решения
можно применять метод вариации
произвольных постоянных. Однако если
в правой части уравнения (32) – многочлен,
либо показательная функция, либо
тригонометрическая функция
 или
или
 ,
либо линейная комбинация перечисленных
функций, то частное решение может быть
найдено методом неопределенных
коэффициентов, не содержащим процесса
интегрирования.
,
либо линейная комбинация перечисленных
функций, то частное решение может быть
найдено методом неопределенных
коэффициентов, не содержащим процесса
интегрирования.
Рассмотрим различные виды правых частей уравнения (32).
1)Правая часть имеет вид
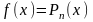 ,
,
где
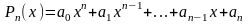 - многочлен степени
- многочлен степени
 .
Тогда частное решение
можно искать в виде
.
Тогда частное решение
можно искать в виде
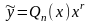 ,
,
где
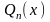 - многочлен той же степени, что и
- многочлен той же степени, что и
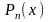 ,
а
,
а
 - число корней характеристического
уравнения, равных нулю.
- число корней характеристического
уравнения, равных нулю.
Пример
1.
Найти общее решение уравнения
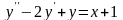 .
.
Общее
решение соответствующего однородного
уравнения имеет вид
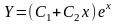 (см. пример 2 в §6). Так как правая часть
уравнения - многочлен первой степени и
ни один из корней характеристического
уравнения
не равен нулю
(см. пример 2 в §6). Так как правая часть
уравнения - многочлен первой степени и
ни один из корней характеристического
уравнения
не равен нулю
 ,
то частное решение ищем в виде
,
то частное решение ищем в виде
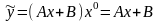 ,
,
где
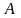 и
и
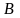 - неизвестные коэффициенты. Дифференцируя
дважды
- неизвестные коэффициенты. Дифференцируя
дважды
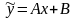 и подставляя
и подставляя
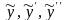 в данное уравнение, найдем
в данное уравнение, найдем
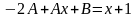 .
.
Приравнивая
коэффициенты при одинаковых степенях
в обеих частях равенства:
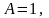
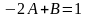 ,
находим:
,
находим:
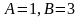 .
Итак, частное решение данного уравнения
имеет вид
.
Итак, частное решение данного уравнения
имеет вид
 а его общее решение
а его общее решение
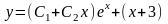 .
.
2) Правая часть имеет вид
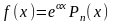 ,
,
где - многочлен степени . Тогда частное решение следует искать в виде
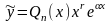 ,
,
где
- многочлен той же степени, что и
,
а
- число корней характеристического
уравнения равных
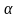 .
Если
.
Если
 ,
то
,
т.е. имеет место случай 1).
,
то
,
т.е. имеет место случай 1).
Пример
2.
Найти общее решение уравнения
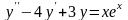 .
.
Характеристическое
уравнение
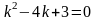 имеет корни
имеет корни
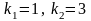 .
Значит, общее решение соответствующего
однородного уравнения имеет вид
.
Значит, общее решение соответствующего
однородного уравнения имеет вид
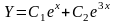 .
В правой части этого уравнения -
произведение многочлена первой степени
на показательную функцию
.
В правой части этого уравнения -
произведение многочлена первой степени
на показательную функцию
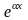 при
при
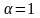 .
Так как среди корней характеристического
уравнения имеется только один корень
.
Так как среди корней характеристического
уравнения имеется только один корень
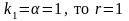 .
В данном случае
.
В данном случае
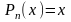 - многочлен первой степени. Поэтому
частное решение данного уравнения ищем
в виде
- многочлен первой степени. Поэтому
частное решение данного уравнения ищем
в виде
 .
.
Дифференцируя и подставляя в уравнение, получаем
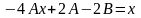 .
.
Приравнивая
коэффициенты при одинаковых степенях
в общих частях равенства:
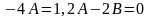 ,
находим
,
находим
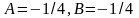 .
Подставляя найденные значения
и
в выражение для
,
получаем частное решение данного
уравнения
.
Подставляя найденные значения
и
в выражение для
,
получаем частное решение данного
уравнения
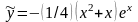 ;
общее решение имеет вид
;
общее решение имеет вид
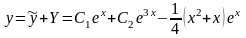 .
.
3) Правая часть имеет вид
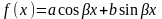 ,
,
где
a,
b
и
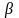 - известные числа. Тогда частное решение
надо искать в виде
- известные числа. Тогда частное решение
надо искать в виде
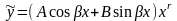 ,
,
где
А
и В
– неизвестные коэффициенты, а r
– число корней характеристического
уравнения, равных
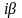 .
.
Пример
3.
Найти общее решение уравнения
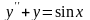 .
.
Характеристическое
уравнение
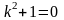 имеет корни
имеет корни
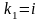 ,
,
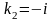 .
Поэтому общее решение соответствующего
однородного уравнения
.
Поэтому общее решение соответствующего
однородного уравнения
 .
В правой части равенства – тригонометрическая
функция
.
В правой части равенства – тригонометрическая
функция
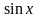 ,
т. е.
,
т. е.
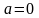 ,
,
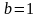 ,
,
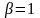 .
Так как
.
Так как
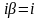 - корень характеристического уравнения,
то
- корень характеристического уравнения,
то
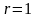 и частное решение надо искать в виде
и частное решение надо искать в виде
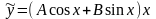 .
.
Дифференцируя и подставляя в уравнение, получаем
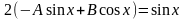 ,
,
откуда
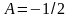 ,
,
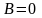 .
Таким образом, частное решение
.
Таким образом, частное решение
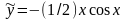 ;
общее решение уравнения
;
общее решение уравнения
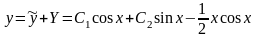 .
.
4) Правая часть имеет вид
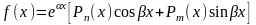 ,
,
где
- многочлен степени
,
а
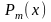 - многочлен степени
- многочлен степени
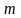 .
Тогда частное решение следует искать
в виде
.
Тогда частное решение следует искать
в виде
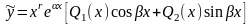 ,
,
где
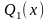 и
и
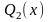 - многочлены степени
- многочлены степени
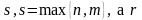 - число корней характеристического
уравнения, равных
- число корней характеристического
уравнения, равных
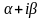 .
.
Пример
4.
Найти общее решение уравнения
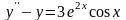 .
.
Здесь
характеристическое уравнение
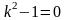 имеет корни
имеет корни
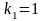 ,
и
,
и
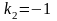 .
Общее решение однородного уравнения
таково:
.
Общее решение однородного уравнения
таково:
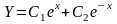 .
В правой части уравнения - произведение
многочлена нулевой степени, показательной
и тригонометрической функций, так что
.
В правой части уравнения - произведение
многочлена нулевой степени, показательной
и тригонометрической функций, так что
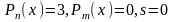 .
Число
.
Число
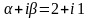 не является корнем характеристического
уравнения, поэтому
не является корнем характеристического
уравнения, поэтому
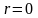 ,
и частное решение ищем в виде
,
и частное решение ищем в виде
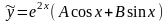 .
.
Дифференцируя и подставляя в уравнение, получаем
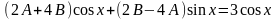 .
.
Приравнивая
коэффициенты при
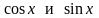 ,
находим
,
находим
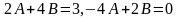 ,
,
откуда
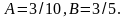 Таким образом, частное решение
Таким образом, частное решение
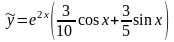 ,
а общее решение уравнения
,
а общее решение уравнения
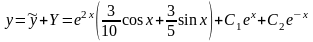 .
.
Теорема.
Если
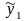 - решение уравнения
- решение уравнения
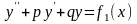 ,
,
а
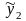 - решение уравнения
- решение уравнения
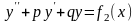 ,
,
то
сумма
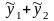 является решением уравнения
является решением уравнения
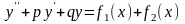 .
.
Пример
5.
Найти общее решение уравнения
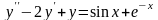 .
.
Характеристическое
уравнение
имеет корни
,
поэтому общее решение соответствующего
однородного уравнения
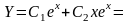
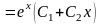 .
.
Так
как правая часть уравнения состоит из
суммы двух функций
и
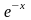 ,
то в соответствии с выше приведенной
теоремой частное решение данного
уравнения можно искать в виде
,
то в соответствии с выше приведенной
теоремой частное решение данного
уравнения можно искать в виде
 ,
,
где
- частное решение уравнения
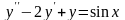 ,
а
- частное решение уравнения
,
а
- частное решение уравнения
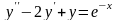 .
.
Сначала
найдем частное решение
.
Так как число
не является корнем характеристического
уравнения
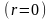 ,
то частное решение
будем искать в виде
,
то частное решение
будем искать в виде
 .
Подставляя
,
.
Подставляя
,
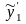 и
и
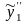 в уравнение
и сравнивая коэффициенты при
и
в уравнение
и сравнивая коэффициенты при
и
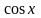 ,
получаем
,
получаем
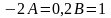 ,
откуда
,
откуда
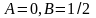 и, следовательно,
и, следовательно,
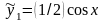 .
.
Теперь
найдем частное решение
.
Будем его искать в виде
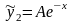 ,
так как число
,
так как число
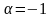 не является корнем характеристического
уравнения. Подставляя
,
не является корнем характеристического
уравнения. Подставляя
,
 и
и
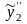 в уравнение
,
имеем
в уравнение
,
имеем
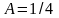 .
Следовательно,
.
Следовательно,
 .
.
Таким образом, частное решение данного уравнения имеет вид
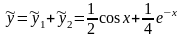 ,
,
а общее решение этого уравнения
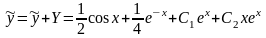 .
.
Контрольные вопросы:
В каком виде ищем частное решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами, если правая часть имеет вид , где - многочлен степени
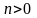 ?
?В каком виде ищем частное решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами, если правая часть имеет вид , где - многочлен степени п?
В каком виде ищем частное решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами, если правая часть имеет вид , а, b и β – числа?
В каком виде ищем частное решение линейного неоднородного уравнения второго порядка с постоянными коэффициентами, если правая часть имеет вид ?
