
- •22 Кафедра математического анализа
- •Глава 1. Дифференциальные уравнения
- •§1 Дифференциальные уравнения первого порядка
- •Уравнение вида
- •§2. Дифференциальные уравнения высших порядков. Основные понятия
- •§3. Уравнения второго порядка, допускающие понижение порядка
- •§4. Линейные однородные дифференциальные уравнения второго порядка
- •§ 5. Линейные неоднородные дифференциальные уравнения второго порядка
- •§6. Линейные однородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •§7. Линейные неоднородные дифференциальные уравнения второго порядка с постоянными коэффициентами
- •Задания для самостоятельного решения
Уравнение вида
|
(5) |
где
 и
и
 - непрерывные функции, называется
линейным
дифференциальным уравнением первого
порядка.
- непрерывные функции, называется
линейным
дифференциальным уравнением первого
порядка.
Если
 ,
то уравнение (5) называется линейным
однородным уравнением.
Если
,
то уравнение (5) называется линейным
однородным уравнением.
Если
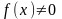 ,
то уравнение (5) называется линейным
неоднородным уравнением.
,
то уравнение (5) называется линейным
неоднородным уравнением.
Для нахождения общего решения уравнения (5) может быть применен метод вариации постоянной.
В этом методе сначала находят общее решение линейного однородного уравнения
|
(6) |
соответствующего данному неоднородному уравнению (5). Уравнение (6) является уравнением с разделяющимися переменными. Разделяя переменные и интегрируя, имеем
 ,
,
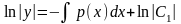 .
.
Отсюда, потенцируя, находим общее решение уравнения (6):
|
(7) |
где
 - произвольная постоянная.
- произвольная постоянная.
Теперь
найдем общее решение уравнения (5) в виде
(7), где
 будем считать не постоянной, а новой
неизвестной функцией от
будем считать не постоянной, а новой
неизвестной функцией от
 ,
т.е. в виде
,
т.е. в виде
|
(8) |
Чтобы
найти функцию
 и, тем самым, решение в виде (8), подставим
функцию (8) в уравнение (5). Получим
и, тем самым, решение в виде (8), подставим
функцию (8) в уравнение (5). Получим
 или
или
|
(9) |
Итак, чтобы функция (8) являлась решением уравнения (5), функция должна удовлетворять уравнению (9). Интегрируя его, находим
 ,
,
где
 - произвольная постоянная. Подставляя
найденное выражение для
в соотношение (8), получаем общее решение
линейного уравнения (5):
- произвольная постоянная. Подставляя
найденное выражение для
в соотношение (8), получаем общее решение
линейного уравнения (5):
|
(10) |
При решении конкретных примеров проще повторять каждый раз все приведенные выше выкладки, чем использовать громоздкую формулу (10).
Пример
3. Найти
общее решение уравнения
 .
.
Данное
уравнение является линейным. Здесь
 ,
,
 .
Решаем сначала соответствующее однородное
уравнение
.
Решаем сначала соответствующее однородное
уравнение
 .
Разделяя переменные
.
Разделяя переменные
 и интегрируя, находим
и интегрируя, находим
 или
или
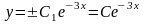 .
.
Ищем
общее решение уравнения
в виде
 .
Дифференцируя, имеем
.
Дифференцируя, имеем
 .
Подставляя в данное уравнение выражения
для
.
Подставляя в данное уравнение выражения
для
 и
и
 ,
получаем
,
получаем
 или
или
 ,
,
откуда
 ,
где
,
где
 - произвольная постоянная. Следовательно,
общее решение данного уравнения имеет
вид
- произвольная постоянная. Следовательно,
общее решение данного уравнения имеет
вид
 или
или
 .
.
Уравнения в полных дифференциалах
Уравнение вида
|
(11) |
где
левая часть представляет собой полный
дифференциал некоторой функции
 в некоторой области
в некоторой области
 ,
называется уравнением
в полных дифференциалах.
,
называется уравнением
в полных дифференциалах.
Если уравнение (11) является уравнением в полных дифференциалах, то его можно записать следующим образом:
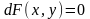 ,
,
где
- такая функция, что
 .
.
Нахождение решения
уравнения (11) сводится к отысканию такой
функции
,
дифференциал которой равен
 .
.
Для того, чтобы выражение было полным дифференциалом некоторой функции , необходимо и достаточно, чтобы
|
(12) |
Допустим,
что условие (12) выполнено. Тогда существует
функция
такая, что
 .
Отсюда
.
Отсюда
|
(13) |
Интегрируя
соотношение
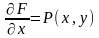 по
,
находим
по
,
находим
|
(14) |
где
 - произвольная функция от
.
Теперь подберем функцию
так, чтобы выполнялось второе из
соотношений (13). Для этого продифференцируем
правую часть равенства (14) по
и производную приравняем
- произвольная функция от
.
Теперь подберем функцию
так, чтобы выполнялось второе из
соотношений (13). Для этого продифференцируем
правую часть равенства (14) по
и производную приравняем
 :
:
|
(15) |
Из
полученного уравнения (15) определяем
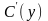 и, интегрируя, находим
.
Подставляя найденную функцию
в соотношении (14), получаем искомую
функцию
.
и, интегрируя, находим
.
Подставляя найденную функцию
в соотношении (14), получаем искомую
функцию
.
Чтобы
выделить из общего решения частное,
удовлетворяющее начальным условиям
 ,
надо в общем решении
,
надо в общем решении
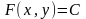 и
заменить начальными значениями. Тогда
и
заменить начальными значениями. Тогда
 и
и
 - искомое частное решение.
- искомое частное решение.
Пример
4. Найти
общее решение уравнения
 и выделить из него частное решение,
удовлетворяющее начальным условиям
и выделить из него частное решение,
удовлетворяющее начальным условиям
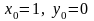 .
.
Здесь
 ,
,
 .
Так как
.
Так как
 ,
,
то
выражение
 является полным дифференциалом некоторой
функции
.
Имеем
является полным дифференциалом некоторой
функции
.
Имеем
|
(16) |
Найдем функцию , используя формулу (15):
 ;
;
 ;
;
 ,
,
 .
.
Подставляя найденное в (16), получаем
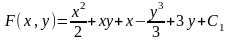 .
.
Данное уравнение принимает вид , а его общее решение определяется уравнением
 .
.
Полагая
 (
( ),
получаем окончательное уравнение,
определяющее неявно общее решение
исходного дифференциального уравнения
),
получаем окончательное уравнение,
определяющее неявно общее решение
исходного дифференциального уравнения
 .
.
Найдем
теперь значение постоянной
 ,
при котором частное решение удовлетворяет
заданным начальным условиям. Имеем:
,
при котором частное решение удовлетворяет
заданным начальным условиям. Имеем:
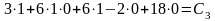 ,
откуда
,
откуда
 ,
и искомое частное решение определяется
уравнением
,
и искомое частное решение определяется
уравнением
 .
.
Контрольные вопросы:
Дайте определение дифференциального уравнения первого порядка.
Что называется решением дифференциального уравнения первого порядка?
Сформулируйте теорему о существовании и единственности решения дифференциального уравнения первого порядка.
В чем заключается задача Коши?
Дайте определение общего и частного решений дифференциального уравнения первого порядка.
В чем заключается геометрический смысл дифференциального уравнения?
Что представляет собой геометрически общее решение уравнения?
Дайте определение дифференциального уравнения с разделяющимися переменными.
Дайте определение линейного дифференциального уравнения первого порядка.
Дайте определение дифференциального уравнения в полных дифференциалах.
