
- •2. Дифференцирование функции одной переменной
- •3. Интегральное исчисление
- •3.1. Первообразная и неопределенный интеграл
- •1. Непосредственное интегрирование.
- •2. Метод подстановки.
- •3. Метод интегрирования по частям.
- •3.2. Определенный интеграл
- •Формулы площадей плоских фигур.
- •2. Формулы объемов тел вращения.
- •4. Дифференциальные уравнения и их применение в медицинской практике
- •5. Основы теории вероятностей
- •Виды случайных событий
- •Полная группа событий
- •Исходы испытания
- •Классическое определение вероятности
- •Статистическое определение вероятности
- •Решение:
- •Решение:
- •Решение:
- •6. Случайные величины и их числовые характеристики
- •6.1. Дискретная случайная величина
- •Свойства математического ожидания
- •Свойства дисперсии
- •Решение:
- •6.2. Непрерывная случайная величина
- •Числовые характеристики непрерывной случайной величины Математическое ожидание
- •Среднее квадратическое отклонение
- •Решение:
- •6.3. Нормальное распределение непрерывной случайной величины (закон Гаусса)
- •7. Элементы математической статистики
- •Оценка параметров генеральной совокупности
- •Литература
- •Содержание
2. Дифференцирование функции одной переменной
Понятие производной
Определение.
Производной
функции
![]() в точке
в точке
![]() называется предел при
называется предел при
![]() отношения приращения функции в этой
точке к приращению аргумента (при
условии, что этот предел существует).
отношения приращения функции в этой
точке к приращению аргумента (при
условии, что этот предел существует).
Производная в
точке
обозначается
![]() или
или
![]() .
.
Итак, по определению производной имеем:
![]()
Процесс нахождения производной называется дифференцированием.
Геометрический
смысл производной:
для данной функции
![]() ее производная
ее производная
![]() для каждого значения
для каждого значения
![]() равна угловому коэффициенту касательной
к графику функции в соответствующей
точке.
равна угловому коэффициенту касательной
к графику функции в соответствующей
точке.
Физический смысл производной: для данной функции , меняющейся со временем х, ее производная есть скорость изменения функции y в данный момент времени х.
Вычисление производной
Правила дифференцирования:
Если функции u и v дифференцируемы в точке х0 , то их сумма дифференцируема в этой точке и
![]()
Примеры: 1)
![]() ;
;
2)
![]() .
.
(производная суммы рана сумме производных).
Если функции u и v дифференцируемы в точке х0 , то их произведение дифференцируемо в этой точке и
![]()
Примеры:
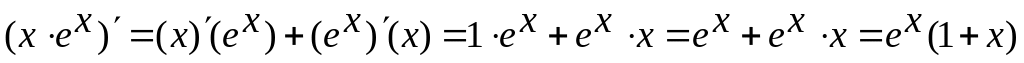 ;
;
 .
.Если функции u и v дифференцируемы в точке х0 и функция v не равна нулю в этой точке, то частное
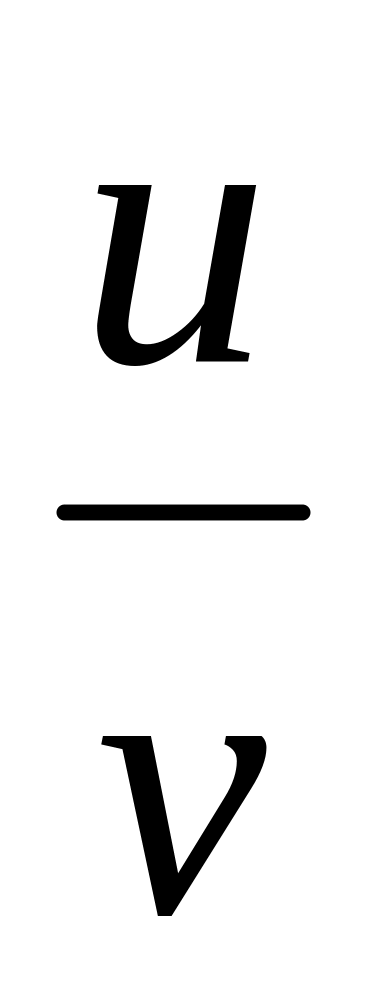 также дифференцируемо в этой точке и
также дифференцируемо в этой точке и
 ;
;
Примеры:
1.
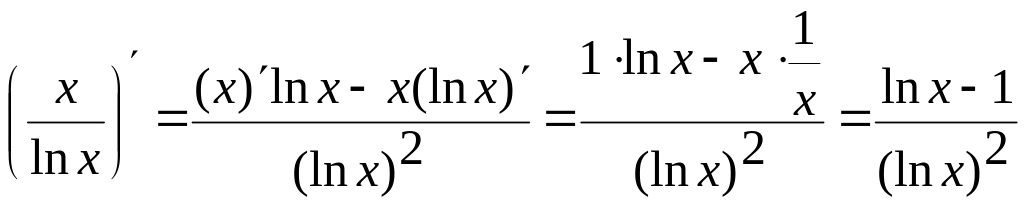 ;
;
2.
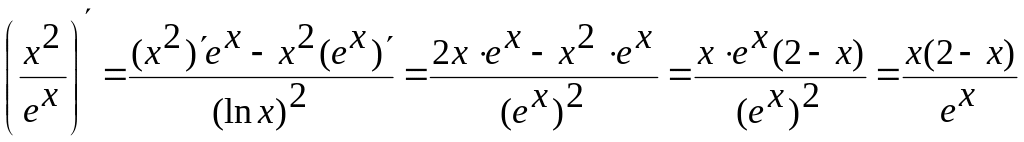 .
.
4) В большинстве
практических случаев процесс
дифференцирования сводится к отысканию
производной сложной функции
![]()
Если в цепи
функциональных зависимостей
![]() аргумент х
является последним, то мы будем называть
его независимой переменной (чтобы
подчеркнуть то обстоятельство, что
изменение этого аргумента не зависит
от поведения других переменных величин).
Правило дифференцирования сложной
функции вытекает из следующей теоремы.
аргумент х
является последним, то мы будем называть
его независимой переменной (чтобы
подчеркнуть то обстоятельство, что
изменение этого аргумента не зависит
от поведения других переменных величин).
Правило дифференцирования сложной
функции вытекает из следующей теоремы.
Теорема.
Если
![]() и
и
![]() –
дифференцируемые функции от своих
аргументов, то производная сложной
функции
–
дифференцируемые функции от своих
аргументов, то производная сложной
функции
![]() существует и равна производной данной
функции у
по промежуточному аргументу и,
умноженной
на производную самого промежуточного
аргумента и
по независимой переменной x,
т. е.
существует и равна производной данной
функции у
по промежуточному аргументу и,
умноженной
на производную самого промежуточного
аргумента и
по независимой переменной x,
т. е.![]() .
.
Примеры:
1.
![]()
2.
![]()
Понятие дифференциала
Если функция
![]() дифференцируема в точке х,
т. е. имеет
в этой точке конечную производную
дифференцируема в точке х,
т. е. имеет
в этой точке конечную производную
![]() то ее приращение
то ее приращение
![]() можно записать в виде
можно записать в виде
![]()
где
![]() .
.
Главная, линейная
относительно
![]() часть
часть
![]() приращения функции называется
дифференциалом
функции и обозначается
приращения функции называется
дифференциалом
функции и обозначается
![]()
![]() или
или
![]() .
.
Производные высших порядков
Производная
![]() называется производной
первой порядка. Производная
от
называется производной
второго порядка (или
второй
производной)
от функции
называется производной
первой порядка. Производная
от
называется производной
второго порядка (или
второй
производной)
от функции
![]() и обозначается
и обозначается
![]() или
или
![]() .
Производная от
называется производной
третьего порядка (или
третьей
производной)
от функции
и обозначается
.
Производная от
называется производной
третьего порядка (или
третьей
производной)
от функции
и обозначается
![]() или
или
![]() и т. д.
и т. д.
Производные n-го
порядка есть производная от производной
(n
- 1)- го порядка, т. е.
![]()
Производные, начиная со второй, называются производными высшего порядка.
Решение типовых задач.
Задание 1.
Используя
определение производной, найти
производную функции
![]() в точке
в точке
![]() .
.
Решение. Придавая аргументу х в точке х0 приращение , найдем соответствующее приращение функции:
![]() Составим
соотношение
Составим
соотношение
![]() .
.
Найдем предел этого отношения при :

Следовательно,
производная функции
![]() в точке
в точке
![]() равна числу
равна числу
![]() ,
что в принятых обозначениях можно
записать так:
,
что в принятых обозначениях можно
записать так:
![]()
Задание 2. Используя правила и формулы дифференцирования, найти производные функций:
Решение.
![]()
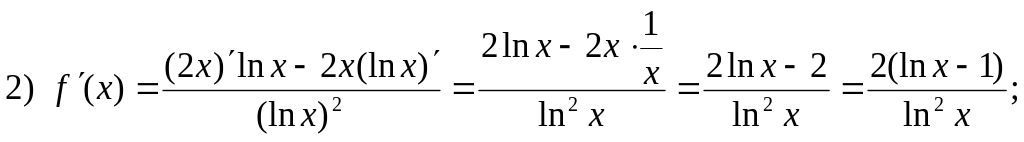
![]()

Задание 3.
Найти дифференциал функции
![]() в точке x=2.
в точке x=2.
Решение:
![]()
Следовательно,
![]()
Задание 4. Найти производные второго порядка от следующих функций:
![]()
Решение:
![]()
![]()
![]()
Упражнения
Задание 1. Используя определение производной, найти производные функций в точке :
Задание 2. Найти производные функций:
![]()
![]()
![]()
![]()
![]()
![]()
Задание 3. Решить задачи.
Написать уравнение касательной к графику функции
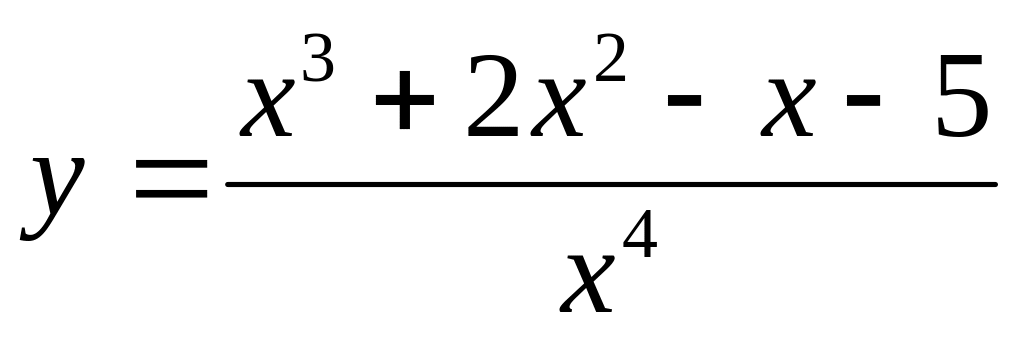 в точке с абсциссой
в точке с абсциссой
 .
.Составить уравнение касательной и нормали к графику кривой
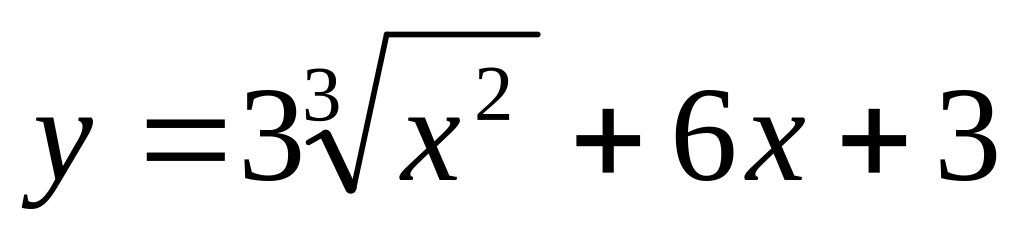 в точке
в точке
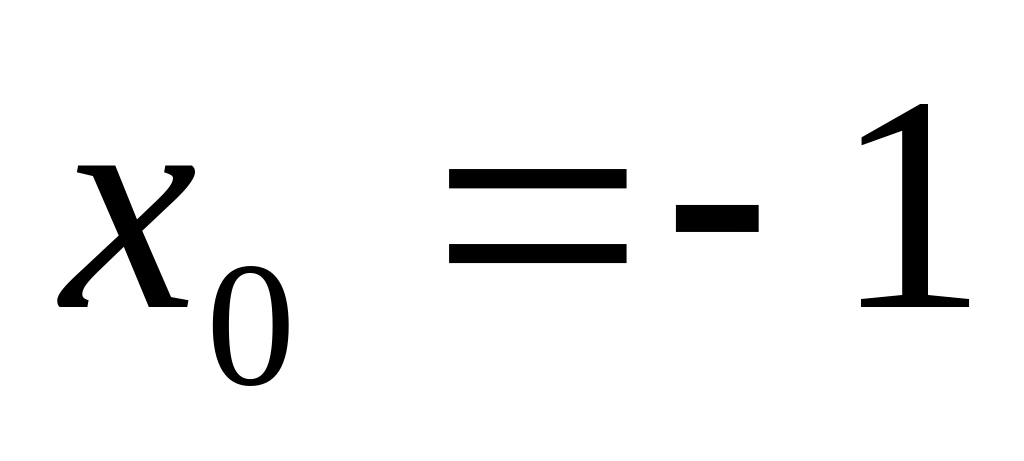 .
.Написать уравнение касательной к графику функции
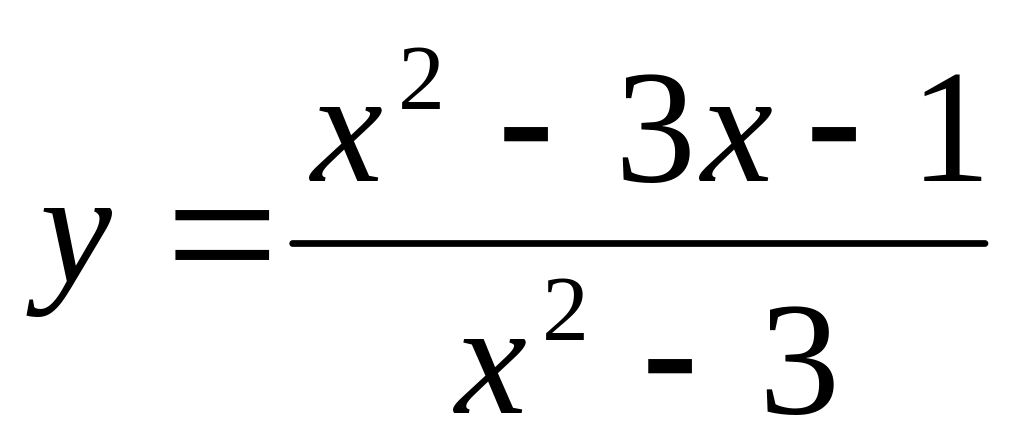 в
точке с абсциссой
.
в
точке с абсциссой
.Составить уравнение касательной к графику кривой
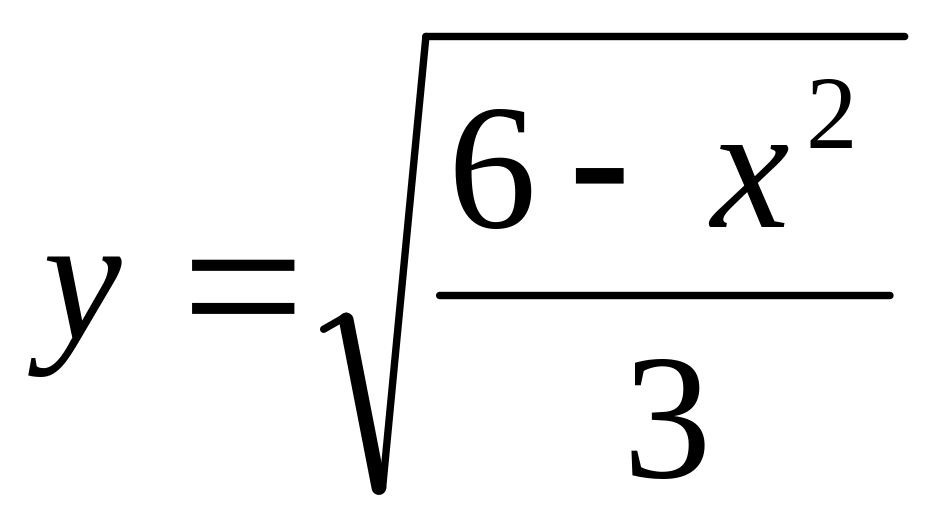 в точке
в точке
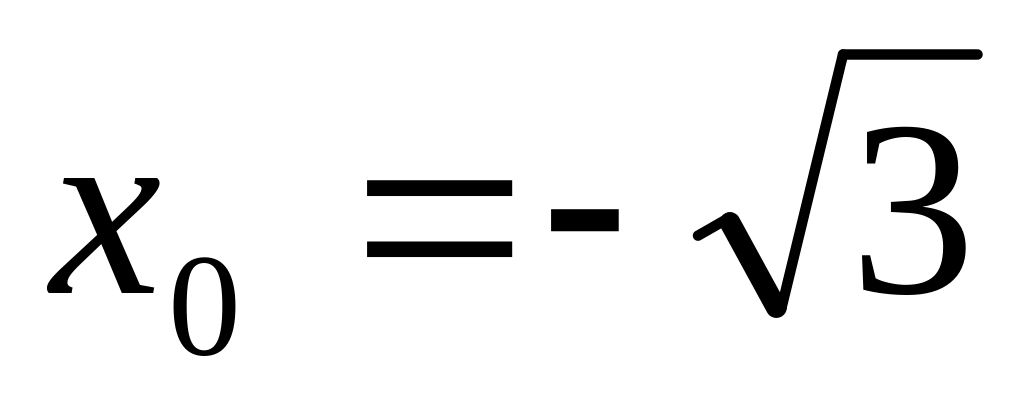 .
.Составить уравнение касательной к графику кривой
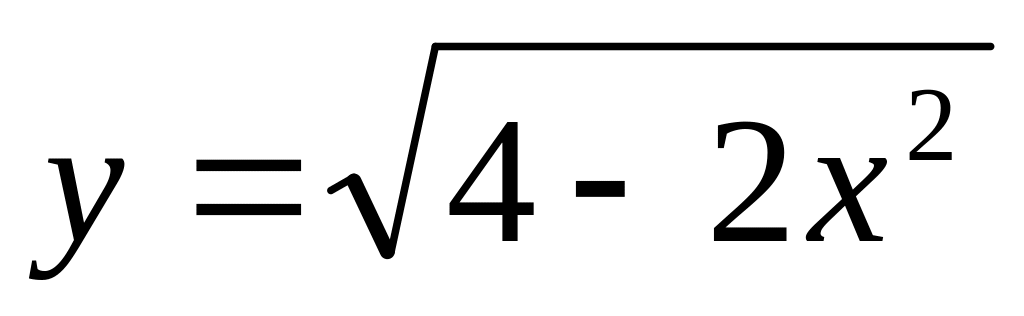 в точке
.
в точке
.Движение летчика при катапультировании из реактивного самолета приближенно можно описать формулой
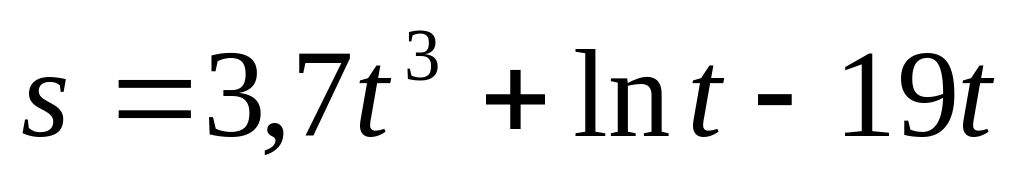 (м).
Определить скорость и ускорение летчика
через 2с после катапультирования
(м).
Определить скорость и ускорение летчика
через 2с после катапультированияПуля, попадая в твердое тело, движется в нем по закону
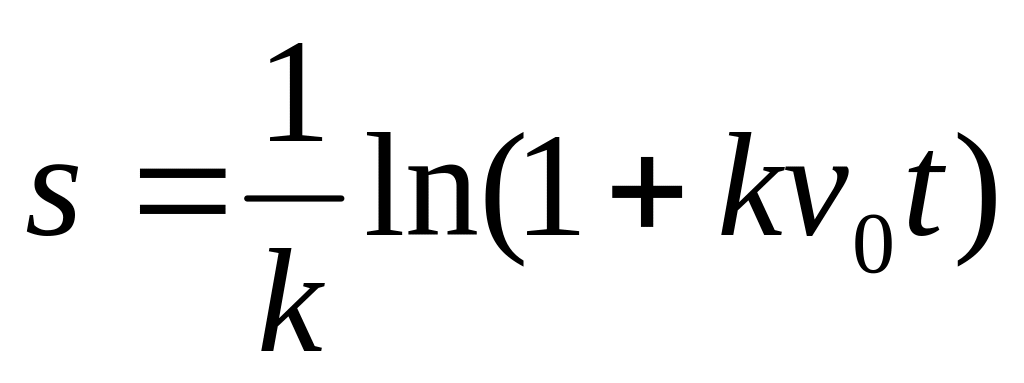 ,
где
,
где

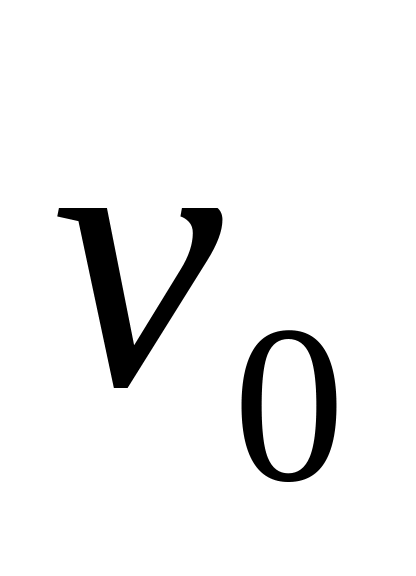 -
скорость, с которой пуля входит в тело,
-
скорость, с которой пуля входит в тело,
 постоянная
величина. Найти ускорение движения
пули.
постоянная
величина. Найти ускорение движения
пули.Зависимость количества вещества
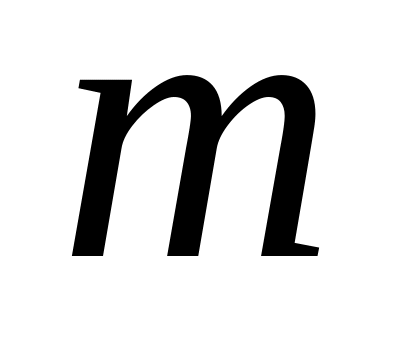 ,
получаемого в химической реакции от
времени
,
получаемого в химической реакции от
времени
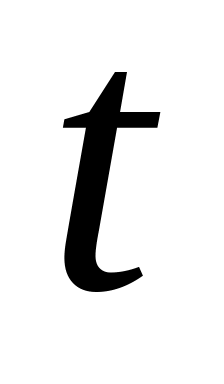 определяется уравнением
определяется уравнением
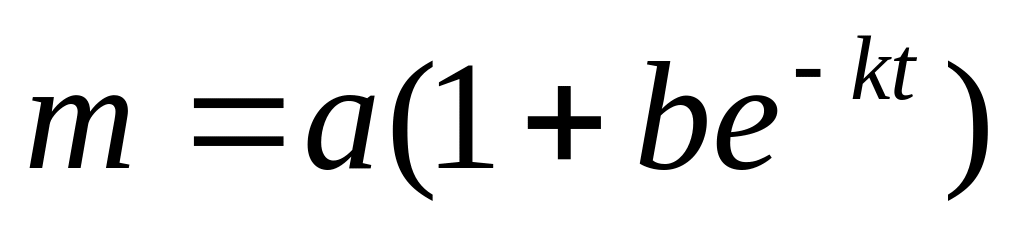 .
Определить скорость реакции.
.
Определить скорость реакции.Вращающееся маховое колесо за секунд поворачивается на угол
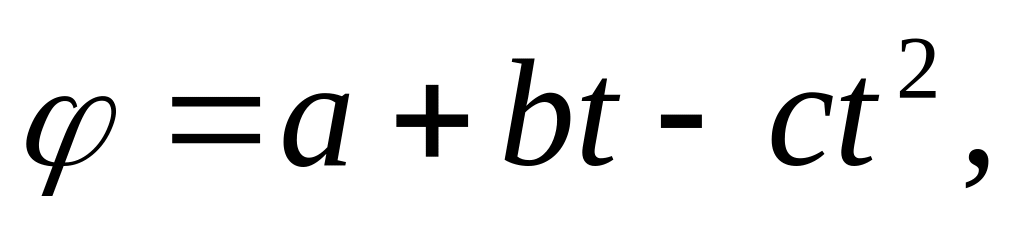 где
где
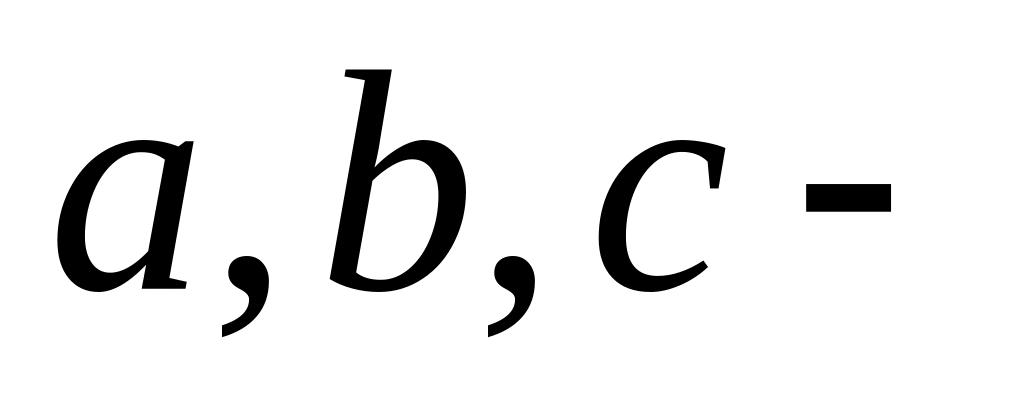 положительные
постоянные. Определить угловую скорость
положительные
постоянные. Определить угловую скорость
 и
ускорение
и
ускорение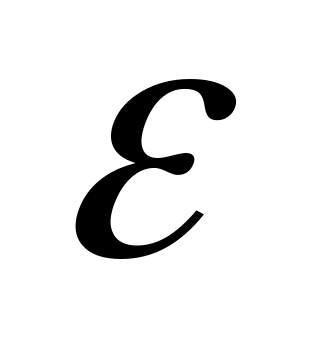 вращения. Когда колесо остановится?
вращения. Когда колесо остановится?Тело движется по закону:
 .
Определить его скорость, ускорение.
.
Определить его скорость, ускорение.Тело движется по прямой
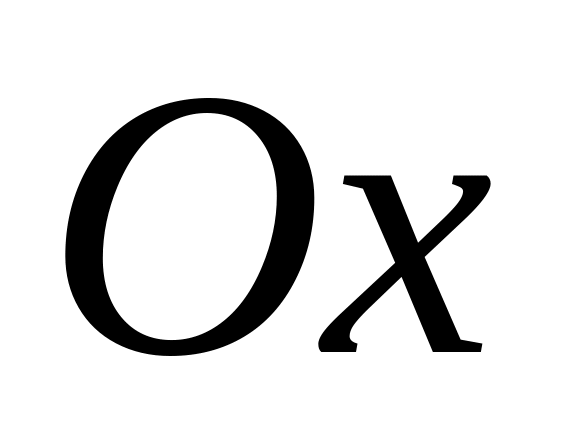 по
закону
по
закону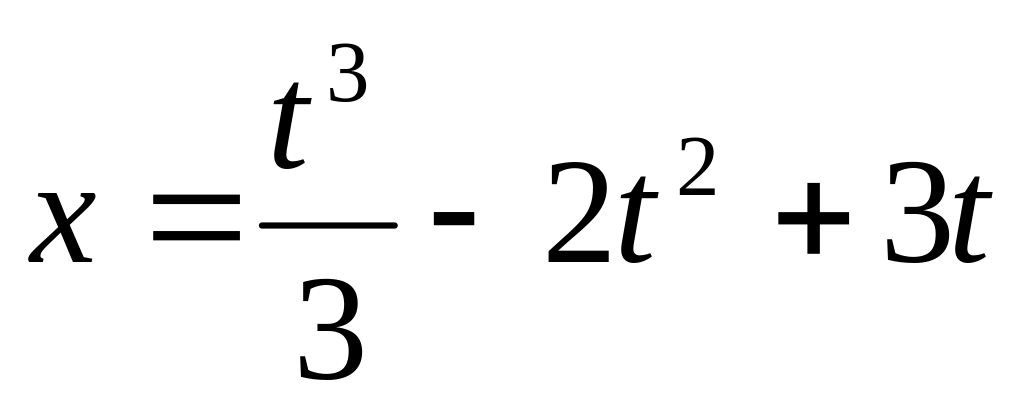 .
Определить скорость и ускорение
движения. В какие моменты тело меняет
направление движения?
.
Определить скорость и ускорение
движения. В какие моменты тело меняет
направление движения?Угол
 ,
на который повернется колесо через
,
на который повернется колесо через
 ,
равен
,
равен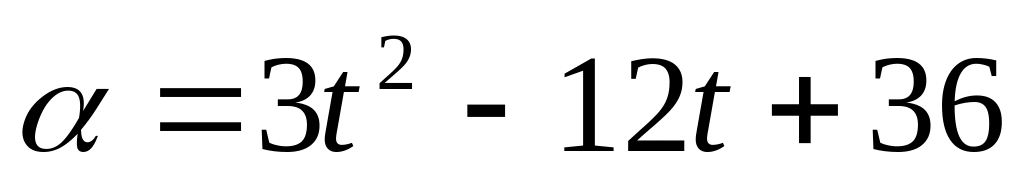 .
Найти угловую
скорость
колеса в момент
.
Найти угловую
скорость
колеса в момент
 и
момент, когда колесо остановится.
и
момент, когда колесо остановится.Показать, что если тело движется по закону
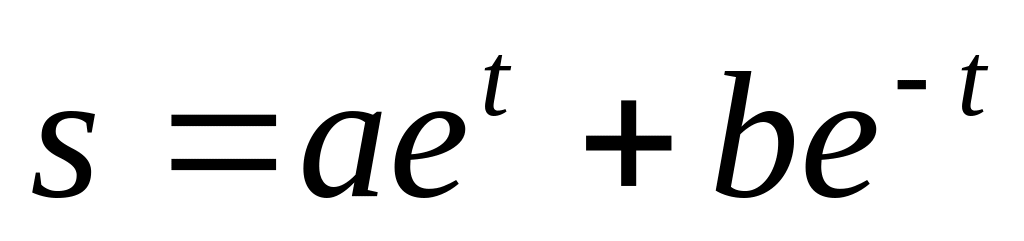 ,
то его ускорение численно равно
пройденному пути.
,
то его ускорение численно равно
пройденному пути.Точка движется прямолинейно, причем
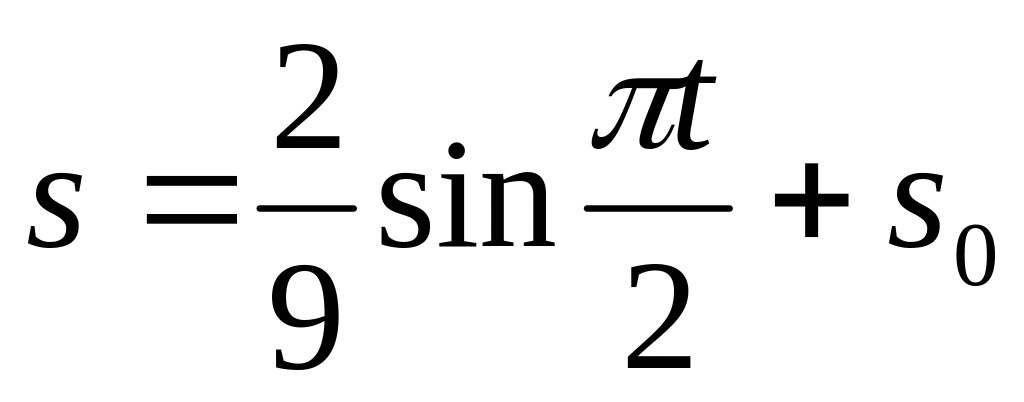 (см/с).
Найти ускорение в конце первой секунды.
(см/с).
Найти ускорение в конце первой секунды.Найти промежутки возрастания и убывания функции
 Построить схематический график этой
функции.
Построить схематический график этой
функции.Исследовать на экстремум и точки перегиба кривую
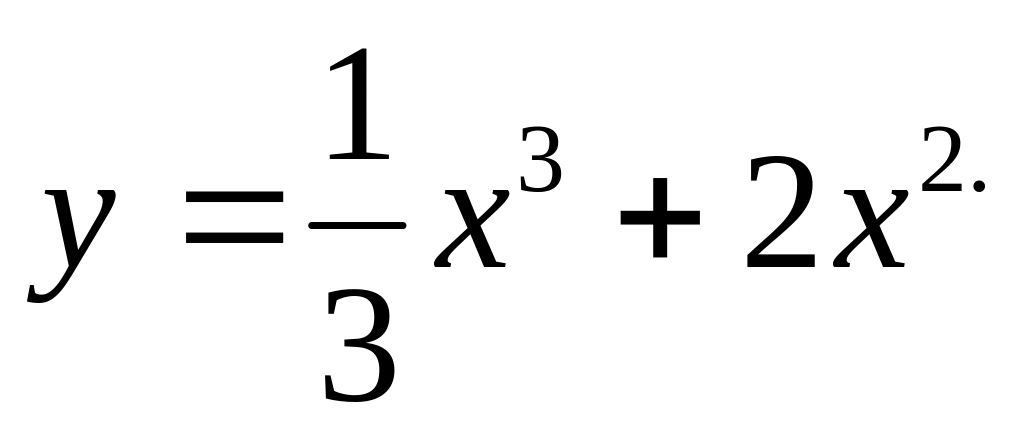 .
Построить схематический график этой
функции.
.
Построить схематический график этой
функции.Исследовать на экстремум и точки перегиба кривую
 Построить схематический график этой
функции.
Построить схематический график этой
функции.
Задание 4. Найти дифференциалы функций:
Задание 5. Найти производные второго порядка от функций:
91.![]()
92.
![]()
93.
![]()
94.
![]()
95.
![]()
96.
![]()
97.
![]()
Задание 6. Найти производные третьего порядка от функций:
98.
![]()
99.
![]()
100.
![]()
101.
![]()
102.
![]()
103.
![]()
104.
![]()
105.
![]()
