Расчет равновесной цены

t
1		= = 4 + 0,54 = 6
2		= = 4 + 0,533,33 = 20,67
3		= = 4 + 0,517,03 = 12,52
4		= = 4 + 0,526,09 = 17,05
5		= = 4 + 0,521,06 = 14,53
6		= = 4 + 0,523,86 = 15,93
7		= = 4 + 0,522,30 = 15,15
8		= = 4 + 0,523,17 = 15,59
9		= = 4 + 0,522,68 = 15,34
10		= = 4 + 0,522,96 = 15,48
11		= = 4 + 0,522,80 = 15,40
12		= = 4 + 0,522,89 = 15,45
13		= = 4 + 0,522,83 = 15,42
14		= = 4 + 0,522,87 = 15,44
15		= = 4 + 0,522,84 = 15,42

Расчет равновесной цены можно закончить на 14-й итерации:

.

Аналогичное значение получаем и по соотношению

Равновесное количество сделок (предложений)

Торговые операции становятся убыточными при количестве сделок

Лекция № 16. Модели потребительского выбора

Пусть потребитель располагает доходом D, который он полностью тратит на приобретение благ (продуктов). Цены благ считаются заданными. Учитывая структуру цен, доход и собственные предпочтения, потребитель приобретает определенные количества благ. Математическая модель поведения потребителя в такой ситуации называется моделью потребительского выбора [2, 9].

Потребитель решает статическую задачу, то есть в модели не учитываются его межвременные предпочтения и возможности делать или расходовать сбережения.

Рассмотрим модель с двумя видами благ. Такая модель удобна возможностью графической интерпретации, сохраняя при этом все принципиальные свойства общей модели.

Потребительский набор - это вектор (x₁, x₂), координата x₁ которого равна количеству единиц первого блага, а координата x₂ равна количеству единиц второго блага.

Выбор потребителя (индивидуума) характеризуется отношением предпочтения, суть которого состоит в следующем. Считается, что потребитель про каждые 2 набора может сказать, что-либо один из них более желателен, чем другой, либо потребитель не видит между ними разницы. Отношение предпочтения транзитивно, т.е. если набор A = (a₁, a₂), предпочтительнее набора B = (b₁, b₂), а набор B предпочтительнее набора C = (c₁, c₂), то набор A предпочтительнее набора C.

На множестве потребительских наборов (x₁, x₂) определена функция U(x₁,x₂) (называемая функцией полезности потребителя), значение которой на потребительском наборе (x₁, x₂) равно потребительской оценке индивидуума для этого набора.

Потребительскую оценку U(x₁, x₂) набора (x₁, x₂) принято называть уровнем (степенью) удовлетворения потребностей индивидуума, если он приобретает или потребляет данный набор (x₁, x₂). Каждый потребитель имеет свою функцию полезности. Если набор предпочтительнее набора В, то U(A) > U(B).

Функция полезности удовлетворяет следующим свойствам.

1. Возрастание потребления одного продукта при постоянном потреблении другого продукта ведет к росту потребительской оценки, т.е. первые частные производные функции полезности по своим аргументам положительны:

, .

Это свойство должно выполняться всегда.

Первые частные производные называются предельными полезностями продуктов: называется предельной полезностью первого продукта, - предельной полезностью второго продукта.

2. Закон убывания предельной полезности: предельная полезность каждого продукта уменьшается, если объем его потребления растет. Математически это означает отрицательность вторых производных:

3. Предельная полезность каждого продукта увеличивается, если растет количество другого продукта. В этом случае продукт, количество которого фиксировано, оказывается относительно дефицитным. Поэтому дополнительная его единица приобретает большую ценность и может быть потреблена более эффективно.

Примечание: Данное свойство не столь очевидно, как первые два, и справедливо не для всех благ. Если блага могут полностью замещать друг друга в потреблении, то свойство 3 не выполняется. Предположение 3 вводится не всегда, но оно гарантирует выпуклость вниз линий безразличия, т.е.

Линия, соединяющая потребительские наборы (x₁, x₂), имеющие один и тот же уровень удовлетворения потребностей индивидуума, называется линией безразличия. Линия безразличия есть не что иное, как линия уровня функции полезности. Множество линий безразличия называется картой линий безразличия. Линии безразличия, соответствующие разным уровням удовлетворения потребностей, не касаются и не пересекаются.

Если линия безразличия расположена выше и правее ("северо-восточнее") линии безразличия , то D₂ > D₁. Верно и обратное. Иными словами чем "северо-восточнее" расположена линия безразличия, тем большему уровню удовлетворения потребности она соответствует. Линия безразличия убывает (является нисходящей) и строго выпукла к началу координат.

Рассмотрим фиксированную линию безразличия . Пусть потребительский набор . При выполнении ряда естественных предположений (непрерывность первых частных производных , и ) справедлива следующая формула: .

Имеем приближенное равенство .

Следовательно .

Отношение показывает, на сколько должен индивидуум увеличить (уменьшить) потребление второго продукта, если он уменьшил (увеличил) потребление первого продукта на одну единицу без изменения уровня удовлетворения своих потребностей (геометрически это означает, что точки принадлежат одной и той же линии безразличия ). Поэтому дробь принято называть нормой замены первого продукта вторым на потребительском наборе (x₁, x₂), а производную (которая равна предельному значению дроби при ) - предельной нормой замены первого продукта вторым (рис.10.1).

Примером функции полезности может служить функция

,

где

Для нее справедливы свойства 1 и 2 функции полезности. Свойство 3 не выполнено, так как смешанные вторые частные производные функции U(x₁,x₂) равны нулю.

Задача потребительского выбора (задача рационального поведения потребителя на рынке) заключается в выборе такого потребительского набора , который максимизирует его функцию полезности при заданном бюджетном ограничении.

Бюджетное ограничение означает, что денежные расходы на продукты не могут превышать денежного дохода, т.е. , где и - рыночные цены одной единицы первого и второго продуктов соответственно, а D - доход индивидуума, который он готов потратить на приобретение первого и второго продуктов. Величины , и D заданы.

Формально задача потребительского выбора имеет вид:

;

при условиях ; .

Допустимое множество (множество наборов благ, доступных для потребителя) представляет собой треугольник, ограниченный осями координат и бюджетной прямой. На этом множестве требуется найти точку, принадлежащую кривой безразличия с максимальным уровнем полезности.

Поиск этой точки можно интерпретировать графически как последовательный переход на линии все более высокого уровня полезности (вправо вверх) до тех пор, пока эти линии еще имеют общие точки с допустимым множеством.

Решение задачи потребительского выбора и его свойства

Набор , который является решением задачи потребительского выбора, принято называть оптимальным для потребителя, или локальным рыночным равновесием потребителя.

Отметим свойства задачи потребительского выбора.

1. Решение задачи сохраняется при любом монотонном преобразовании функции полезности U(x₁, x₂). Таким монотонным преобразованием может быть умножение функции полезности на некоторое положительное число, возведение ее в положительную степень, логарифмирование по основанию, большему единицы.

Поскольку значение было максимальным на всем допустимом множестве, оно остается таковым и после монотонного преобразования функции полезности (допустимое множество, определяемое бюджетным ограничением, остается неизменным). Отметим, что свойство 1 должно присутствовать у любой функции полезности; свойства 2 и 3 могут при ее монотонных преобразованиях теряться или приобретаться.

2. Решение задачи потребительского выбора не изменится, если все цены и доход увеличиваются (уменьшаются) в одно и то же число раз .

Это равнозначно умножению на положительное число  обеих частей бюджетного ограничения , что дает неравенство, эквивалентное исходному. Поскольку ни цены, ни доход D не входят в функцию полезности, задача остается той же, что и первоначально.

В приведенной постановке задача потребительского выбора является задачей нелинейного программирования. Однако, если на каком-то потребительском наборе (x₁, x₂) бюджетное ограничение будет выполняться в виде строгого неравенства, то мы можем увеличить потребление какого-либо из продуктов и тем самым увеличить функцию полезности. Следовательно, набор , максимизирующий функцию полезности, должен обращать бюджетное ограничение в равенство, т.е. .

Графически это означает, что решение задачи потребительского выбора должно лежать на бюджетной прямой, которую удобнее всего провести через точки пересечения с осями координат, где весь доход тратится на один продукт: и .

Будем также считать, что в оптимальной точке условия положительности величин x₁ и x₂ выполняются автоматически, вытекая из свойств функции . Как правило, это действительно так.

В то же время, если условия неотрицательности переменных не включать в явном виде в условие задачи, то она становится существенно проще с математической точки зрения.

Итак, задачу потребительского выбора можно заменить задачей на условный экстремум, так как решение этих двух задач одно и то же:

при условиях ; .

Для решения задачи на условный экстремум применим метод Лагранжа.

1) Выписываем функцию Лагранжа

.

2) Находим ее первые частные производные по переменным x₁, x₂,  и приравниваем эти частные производные к нулю:

.

Исключив из полученной системы трех уравнений с тремя неизвестными величину , получим систему двух уравнений с двумя неизвестными :

; .

Решение этой системы есть решение задачи потребительского выбора (за исключением так называемых угловых решений, которые здесь не рассматриваются).

Подставив решение в левую часть равенства получим, что в точке локального рыночного равновесия индивидуума отношение предельных полезностей продуктов равно отношению рыночных цен , и на эти продукты: .

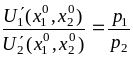В связи с тем, что отношение 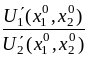равно предельной норме замены первого продукта вторым в точке локального рыночного равновесия , то следует, что эта предельная норма равна отношению рыночных цен на продукты. Приведенный результат играет важную роль в экономической теории.

Геометрически решение можно интерпретировать как точку касания линии безразличия функции полезности с бюджетной прямой . Это определяется тем, что отношение показывает тангенс угла наклона линии уровня функции полезности, а отношение – представляет тангенс угла наклона бюджетной прямой. Поскольку в точке потребительского выбора (или локального рыночного равновесия) они равны, в этой точке происходит касание данных двух линий. Следовательно 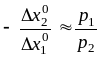, т.е. отношение (со знаком минус) конечных (относительно небольших) изменений и объемов продуктов в локальном рыночном равновесии приближенно равно отношению рыночных цен p₁, p₂ на продукты.

Последнее равенство позволяет давать приближенные оценки отношению рыночных цен, если известны конечные изменения объемов продуктов относительно потребительского набора, приобретенного потребителем, т.е. набора, который естественно следует толковать в качестве оптимального для потребителя.

Координаты решения задачи потребительского выбора есть функции параметров p₁, p₂ и D: , .

Полученные функции называются функциями спроса на первый и второй продукты. Важным свойством функций спроса является их однородность нулевой степени относительно цен и дохода, т.е. значения функций спроса инвариантны по отношению к пропорциональным изменениям цен и дохода (для любого числа ):

; .

Это означает, что если все цены и доход изменятся в одно и то же число раз, величина спроса на продукт (первый или второй - безразлично) останется неизменной.

Общая модель потребительского выбора

Пусть задана целевая функция предпочтения потребителя (где - количество -го блага), вектор цен и доход . Записав бюджетное ограничение и ограничения на неотрицательность, получаем задачу [9]:

;

при условиях

.

Будем, как и ранее, считать, что неотрицательность переменных обеспечивается свойствами целевой функции и бюджетного ограничения. В этом случае можно записать функцию Лагранжа и исследовать ее на безусловный экстремум. Функция Лагранжа будет иметь матричный вид

.

Необходимые условия экстремума - равенство нулю частных производных: для всех i от единицы до n ; .

Отсюда следует, что для всех i и в точке локального равновесия выполняется равенство . Или в другой форме: .

Это означает, что дополнительная полезность, приходящаяся на дополнительную единицу денежных затрат, в точке оптимума одинакова по всем видам благ.

Модель Р.Стоуна

Получим функцию спроса на примере конкретной функции потребительского предпочтения, называемой функцией Р.Стоуна и имеющей вид:

.

Здесь a_i - минимально необходимое количество i-го блага, которое приобретается в любом случае и не является предметом выбора.

Для того чтобы набор (a_i) мог быть полностью приобретен, необходимо, чтобы доход был больше количества денег, требуемого для покупки этого набора: . Коэффициенты степени b_i > 0 характеризуют «ценность» благ для потребителя.

Модель Р.Стоуна имеет вид:

;

; .

Решение находим методом Лагранжа. Приравняв нулю частные производные функции Лагранжа по переменным х_i, получаем для всех i:

. Отсюда получаем: .

К этим условиям добавляется равенство , выполнение которого эквивалентно равенству нулю частной производные функции Лагранжа по переменной . Умножив каждое i-ое условие на  и просуммировав их по i, получим: .

Поскольку в точке оптимума бюджетное ограничение выполняется как равенство, заменим на D. Получим

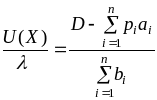
Отсюда имеем функцию спроса .

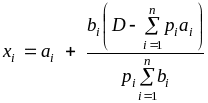Частные случаи модели Р.Стоуна

Если все a_i = 0, а все b_i равны между собой, получаем , т.е. доход делится на равные части и спрос на i-й товар рассчитывается как частное от деления полученной суммы денег на его цену.

В данном случае мы видим, что спрос растет при росте дохода с эластичностью, равной единице, и уменьшается с ростом цены с эластичностью, равной минус единице. Тем самым каждый товар в этой модели является нормальным и ценным. Кроме того, спрос растет до бесконечности при бесконечном росте дохода - в этом смысле каждый товар является "предметом роскоши".

Для того чтобы описать более разнообразные формы поведения спроса на различные товары, модель должна включать другие, более сложные виды целевой функции предпочтения.

Например, при функции предпочтения (где - параметры) функция спроса имеет вид (типичная функция спроса для предметов первой необходимости) и (типичная функция спроса для предметов роскоши).

Взаимозаменяемость благ. Эффекты компенсации

Если функция спроса имеет вид (или, при неравных между собой 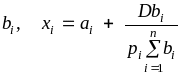), то спрос на i-й товар не зависит от цены на любой j-й товар.

Перекрестные функции спроса от цен характеризуют такие свойства товаров, как взаимозаменяемость и взаимодополняемость. Если при росте цены на товар i, при снижении спроса на i-й товар, растет спрос на j-й товар - эти товары взаимозаменяемы (например, картофель - крупы; чай - кофе). Наоборот, если спрос на j-й товар также падает, - они взаимодополняемы.

Заметим, что реальная взаимозаменяемость может искажаться общим снижением благосостояния при росте цены i-го блага: j -ое благо может заменять i-е в потреблении, но спрос на него может не расти, поскольку снизилось общее благосостояние потребителя.

Для снятия этого искажения используют понятие компенсированного изменения цены, то есть такого, которое сопровождается увеличением дохода потребителя, позволяющим ему поддерживать прежний уровень благосостояния. Практически компенсированное изменение цены изображается следующим образом (рис.10.2).

Пусть цена первого блага повысилась c до тогда бюджетная прямая из положения 1 перейдет в положение 2. Точка А на линии безразличия , касающейся первоначального бюджетного ограничения, будет заменена новой точкой оптимума В, где новая линия безразличия , касается новой бюджетной прямой. Если мы хотим компенсировать потребителю потерю благосостояния, то увеличим его доход так, чтобы новая бюджетная прямая 3 (параллельная линии 2) коснулась в некоторой точке С прежней линии безразличия .

Направленный отрезок АС показывает "эффект замены" при росте цены, то есть изменение структуры спроса при условии поддержания прежнего уровня благосостояния. Направленный отрезок СВ отражает "эффект дохода", то есть изменение потребительского спроса при сохранении соотношения цен благ и изменении уровня дохода. Общий результат роста цены (при отсутствии компенсации) выражается направленным отрезком АВ.

Для формального анализа компенсационных эффектов рассмотрим вначале две задачи.

Пример 10.1. Пусть целевая функция потребителя (ЦФП) зависит от двух благ и следующим образом: . Пусть цены благ равны, соответственно, 10 и 2, а доход потребителя - 60. Тогда, согласно полученной формуле функции спроса, . Пусть теперь р меняется с 2 до 7. Каков необходимый размер компенсации?

Чтобы приобрести прежний оптимальный набор, потребителю необходимо дополнительно (7 - 2)  15 = 75 денежных единиц.

Однако прежняя структура потребления не будет оптимальной при новых ценах, и минимальная необходимая компенсация будет меньше, чем 75.

Пусть потребитель получает дополнительно количество денег М. Тогда при новых ценах его спрос на первое и второе блага будет равен:

.

Целевая функция будет равна , и это выражение должно равняться начальному . Отсюда , что существенно меньше, чем 75.

Теперь решим задачу в более общем виде. Пусть по-прежнему ; цены благ равны , и , а доход . Очевидно, что

.

Пусть теперь цена выросла в К раз (К > 1), и при этом потребитель получает необходимую компенсацию. Новый размер дохода обозначим через , спрос - . Очевидно, и условие компенсации , откуда .

Итак, спрос на первый товар в случае с компенсацией сократится в раз (а не в К раз, как без нее), а спрос на второй товар в раз вырастет. В случае роста цены второго товара ситуация будет полностью симметричной. Таким образом, при , или ,.

Индекс сотр означает, что перекрестная частная производная спроса рассчитывается при необходимой для поддержания прежнего уровня благосостояния компенсации дохода. Условие компенсации снимает "эффект дохода", оставляя лишь"эффект замены", что позволяет более точно определить понятие взаимозаменяемости и взаимодополняемости благ и оценивать эти характеристики.

Блага i и j называются взаимозаменяемыми, если

и (эти два условия равносильны),

и взаимодополняемыми, если и .

Рассчитаем теперь эти частные производные для рассматриваемой задачи, когда растет в К раз. В этом случае приращение

. Отсюда

;

.

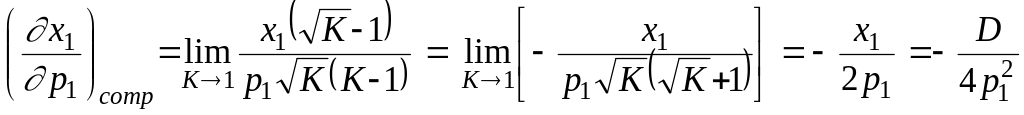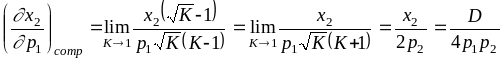Последняя величина положительна, что свидетельствует о взаимозаменяемости благ в рассматриваемой задаче.

Уравнение Слуцкого

Одним из основных в теории потребительского выбора является уравнение Слуцкого, опубликованное российским математиком Е.Е.Слуцким в 1915 году. Это уравнение позволяет увязать действие эффекта замены и эффекта дохода с результирующим изменением спроса. Уравнение Слуцкого имеет вид:

.

Первое слагаемое в правой части описывает действие эффекта замены, второе - действие эффекта дохода, выраженное в тех же единицах измерения (множитель приводит их к одной размерности). Слева записано результирующее воздействие на спрос, складывающееся из изменения структуры спроса и общего его изменения при изменении уровня реального дохода. Для ценных товаров величина , т.е. спрос растет при росте дохода. В этом случае, согласно уравнению Слуцкого, : если спрос растет, то он растет больше при наличии компенсации, если падает - то в меньшей степени. Может оказаться и так, что , но , то есть товары i и j взаимозаменяемы, но представляются взаимодополняемыми без учета компенсации.

Уравнение Слуцкого может рассматриваться как при разных, так и при совпадающих i и j.

Из первых двух свойств функции полезности потребителя следует, что (на графике это обусловлено выпуклостью линий уровня функции полезности). Если оказывается, что (спрос на товар растет при росте цены - такие товары называются товарами Гиффина), то отсюда вытекает, что - то есть это обязательно малоценный товар.

Проверим уравнение Слуцкого для рассмотренной выше задачи потребительского выбора с функцией полезности .

Было получено:

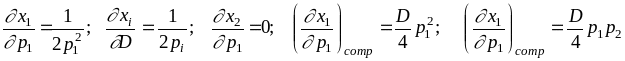
Отсюда ; и .

В обоих случаях уравнения Слуцкого (при i = j и при i  j) здесь выполнены.

Уравнение Слуцкого может быть использовано для нахождения , то есть для расчета эффекта замены и оценки взаимозаменяемости или взаимодополняемости благ, поскольку частные производные без компенсации рассчитываются значительно легче.

Рассмотрим эластичности функции спроса. Эластичность спроса по цене равна ; эластичность спроса по доходу .

Для функции эластичность .

Из свойств функции спроса можно получить равенство , т.е. нулю должна равняться сумма всех эластичностей спроса по ценам и доходу.

Покажем, что если в задаче потребительского выбора всего два товара, то они обязательно являются взаимозаменяемыми. Для этого воспользуемся тем, что и положительностью частных производных функции полезности.

Предположим, что выросла цена 1-го товара .

Поскольку , спрос на этот товар при условии компенсации падает. Если бы при этом упал спрос и на второй товар, то мы получили бы точку, в которой обоих товаров меньше, чем в начальной.

Следовательно, в этой точке значение функции полезности должно быть также меньше (а мы знаем, что в условиях компенсации оно равно начальному). Следовательно, спрос на второй товар при условии компенсации должен вырасти (т.е. ) и он является взаимозаменяемым с первым товаром.

Пример 10.2. На основании данных о потреблении взаимозаменяемых и взаимодополняемых продуктов x₁ и x₂ в различном сочетании i, их цене и , полезности U и бюджете (доходах) потребителя D построить кривую безразличия и определить оптимальный план потребления названных продуктов.

Исходные данные имеют вид:

i	х1i	i	х2i
1	2,9	1	13,5
2	3,0	2	12,0
3	5,0	3	7,5
4	7,0	4	6,0
5	10,0	5	5,0
6	12,0	6	4,5
7	12,3	7	4,6

U = 18; P₁ = 5; P₂ = 10,3; D = 100.

Решение. В нашей задаче продукты х₁ и х₂ являются взаимозаменяемыми и взаимодополняемыми, т.е. функция смешанная. Поэтому можно воспользоваться моделью неоклассической функции полезности, которая имеет вид , где .

Чтобы убедиться в правильности предположения о форме связи, следует графически изобразить изучаемую зависимость в системе координат по данным о потреблении продуктов х₁ и х₂. По виду графика можно предположить, что зависимость между x₁ и x₂ имеет вид при .

Решение задачи по построению кривой безразличия заключается в определении параметров функции b₁ и b₂. Параметры кривой безразличия b₁ и b₂ отражают степень полезности каждого из продуктов x₁ и x₂.

Определив параметры b₁ и b₂, зная одну из переменных - количество потребления продукта x₁, всегда можно определить вторую переменную x₂ так, чтобы обеспечить максимум полезности от потребления продуктов

.

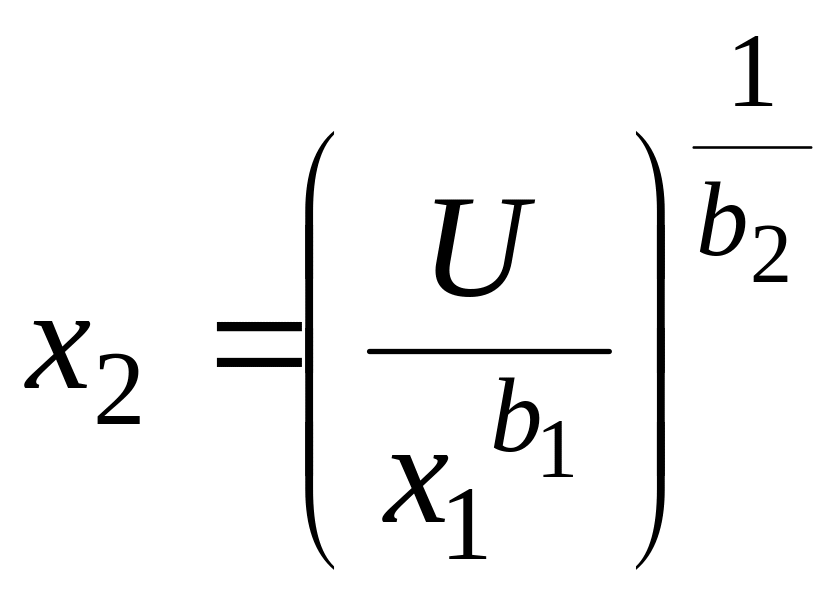Для расчета параметров функции целесообразно ее линеаризовать посредством логарифмирования.

Имеем .

Обозначим и запишем .

Отсюда .

Обозначив , можно записать .

Для определения коэффициентов A и B обычно применяют метод наименьших квадратов:

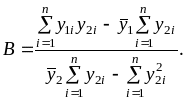
Учитывая, что определяют и .

Проверяют правильность расчетов и определяют расчетную кривую безразличия 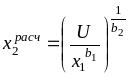, отражающую отношения предпочтения, характерные для отдельного индивидуума.

На графике оптимальный план потребления соответствует точке касания бюджетной прямой и кривой безразличия.

Ее координаты, т.е. значения , определяются путем нахождения частных производных функций

После некоторых преобразований имеем

Полученные функции и есть функции спроса. Они отражают оптимальный размер потребления продуктов, обеспечивающий максимум полезности в рамках бюджетного ограничения при заданных ценах.

При расчете величин A и B можно воспользоваться таблицей вспомогательных расчетов.

Ниже приводятся расчеты для имеющихся данных.

Таблица 10.1

Расчет функции безразличия

i	х1i		х2i		y1iy2i	y2i2
1	2,9	1,065	13,5	2,603	2,772	6,776
2	3,0	1,099	12,0	2,485	2,731	6,175
3	5,0	1,609	7,5	2,015	3,242	4,060
4	7,0	1,946	6,0	1,792	3,487	3,211
5	10,0	2,303	5,0	1,609	3,706	2,589
6	12,0	2,485	4,5	1,504	3,737	2,262
7	12,3	2,509	4,6	1,526	3,829	2,329

Определим коэффициенты A и B методом наименьших квадратов:

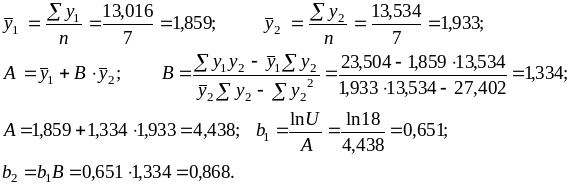
= = 2.890; = 3.329; = 0.75.