
- •С.А. Воробьев
- •Конспект лекций
- •Лекция № 1. Введение. Современное состояние и развитие экономико-математического моделирования
- •Лекция № 2. Классификация экономико-математических моделей
- •Лекция № 3. Методология математического моделирования экономических систем. Особенности моделирования экономических процессов
- •Лекция № 4. Основные принципы описания производственно - технологического процесса экономических систем. Этапы исследования экономических процессов
- •Лекция № 5. Балансовые модели. Статические балансовые модели
- •Лекция № 6. Анализ статистических балансовых моделей
- •Лекция № 7. Динамические балансовые модели
- •Лекция № 8. Модели экономической динамики. Описание моделей экономической динамики
- •Лекция № 9. Исследование моделей экономической динамики
- •Лекция № 10. Оптимальные траектории. Характеристика оптимальных траекторий
- •Лекция № 11. Вероятностно-статистические модели в экономике
- •Основные предельные положения теории вероятностей сводятся к следующему.
- •Ряд распределения системы двух дискретных величин
- •Лекция № 12. Модели массового обслуживания
- •Выходной поток требований
- •Классификация систем массового обслуживания
- •Лекция № 13. Модели изучения и прогнозирования спроса
- •Лекция № 14. Модели управления товарными запасами
- •Лекция № 15. Модели равновесия рынка
- •Расчет равновесной цены
- •Лекция № 16. Модели потребительского выбора
- •Лекция № 17. Маржинальный анализ. Заключение
- •Маржинального анализа для примера 11.1
Ряд распределения системы двух дискретных величин
-
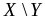
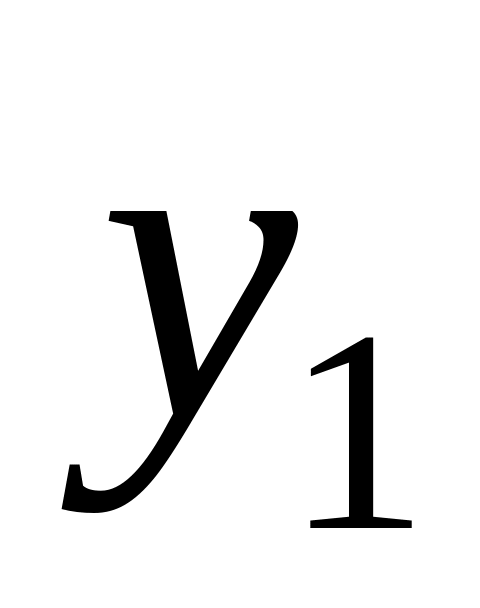
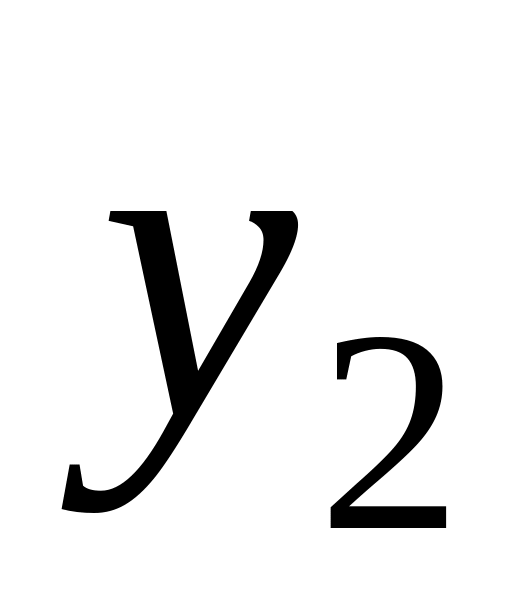
...
...
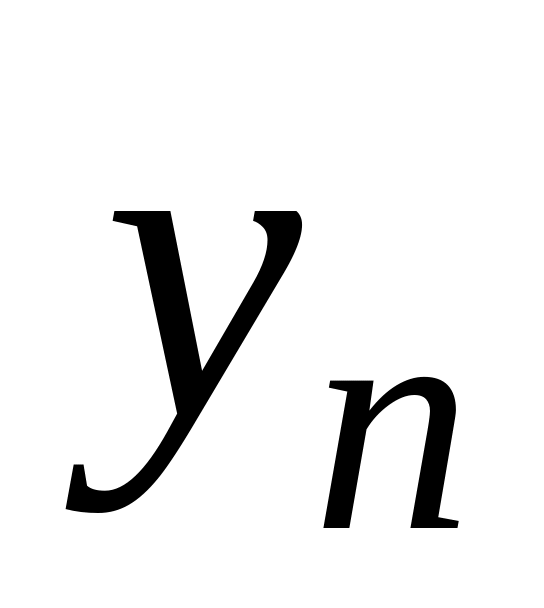

...
...
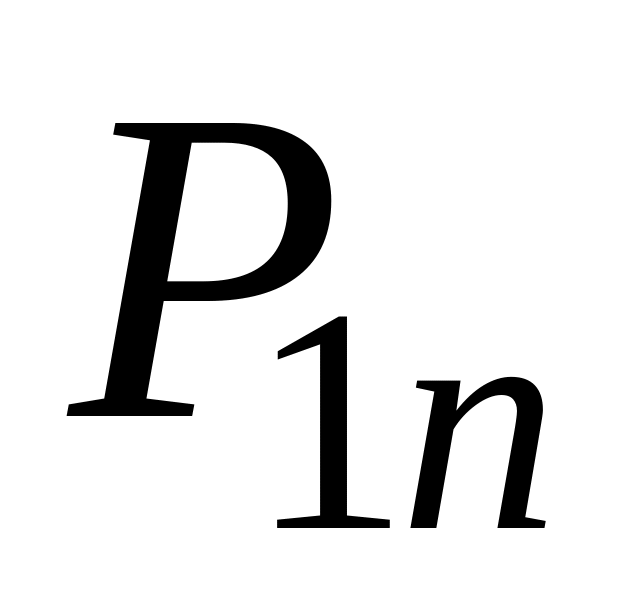
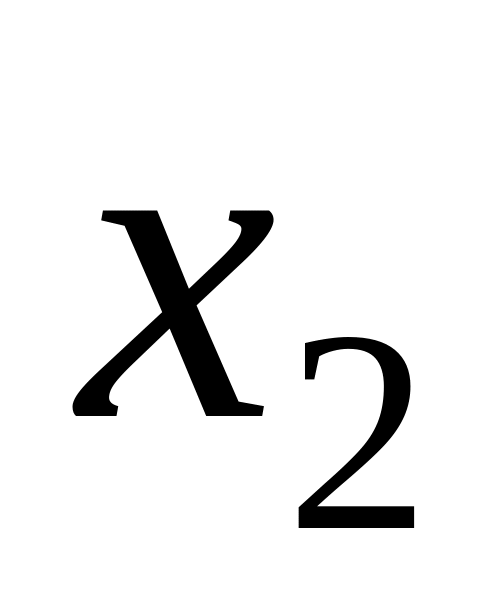
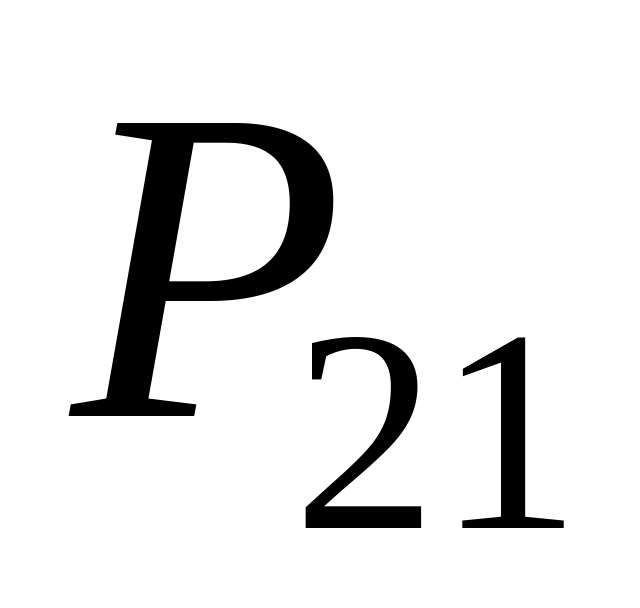

...
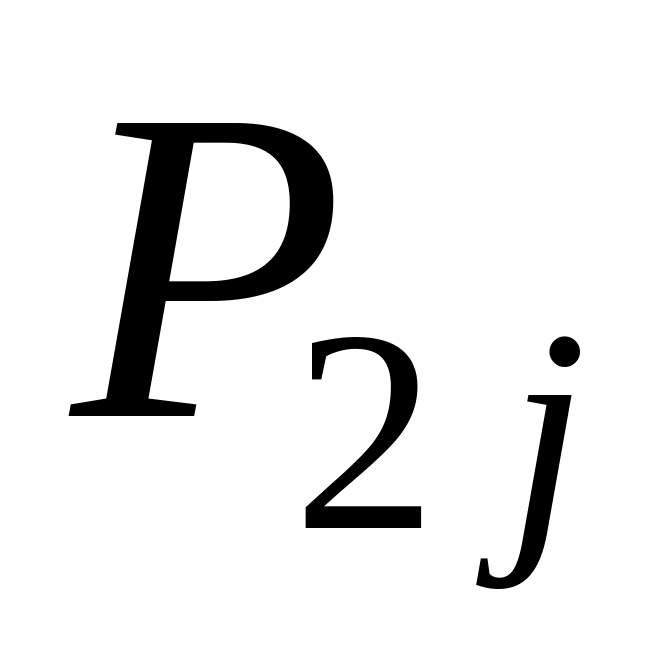
...
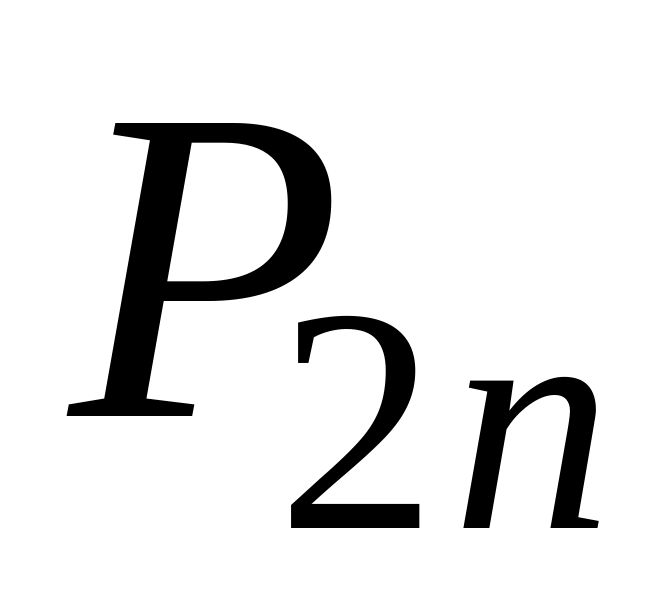
...
...
...
...
...
...
...
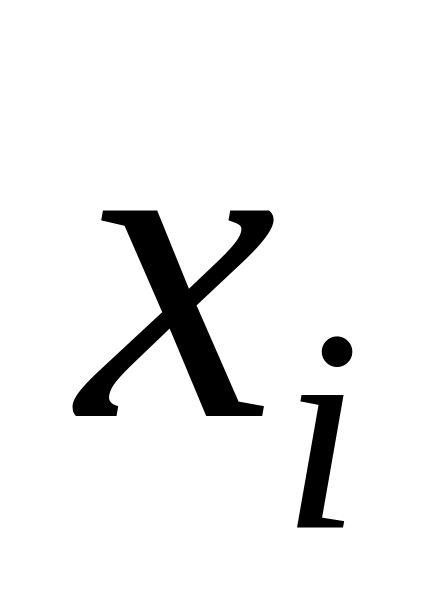
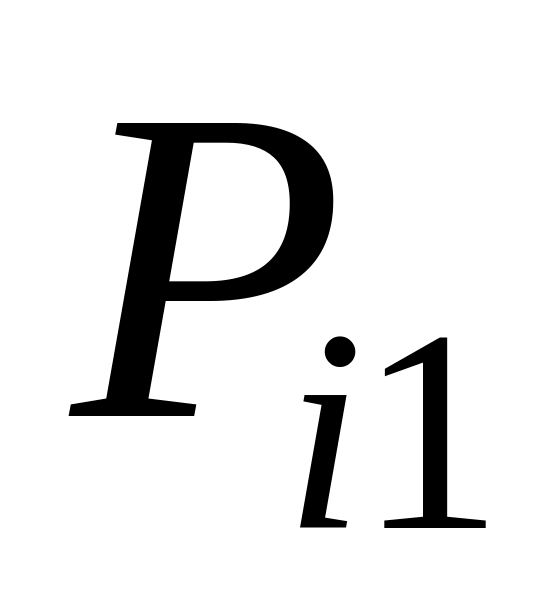
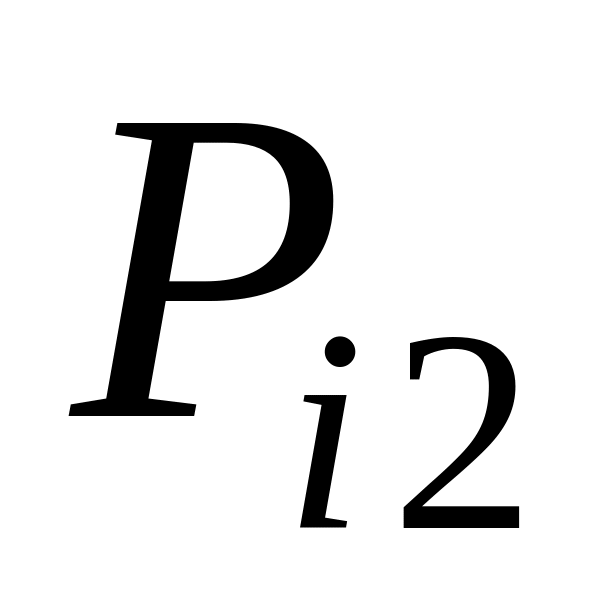
...
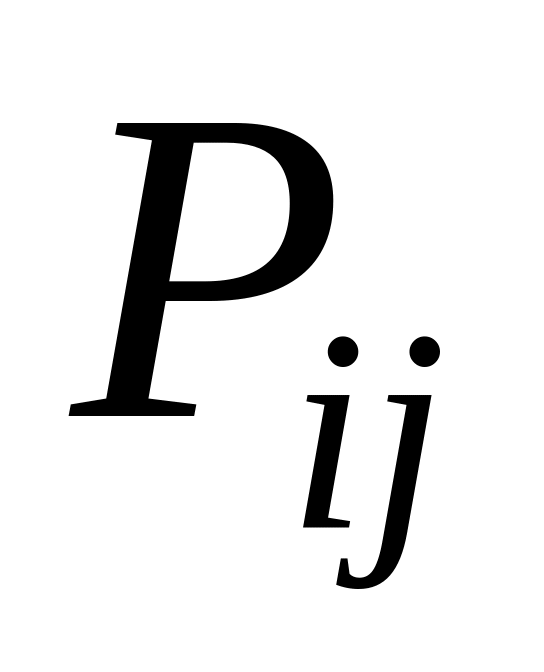
...
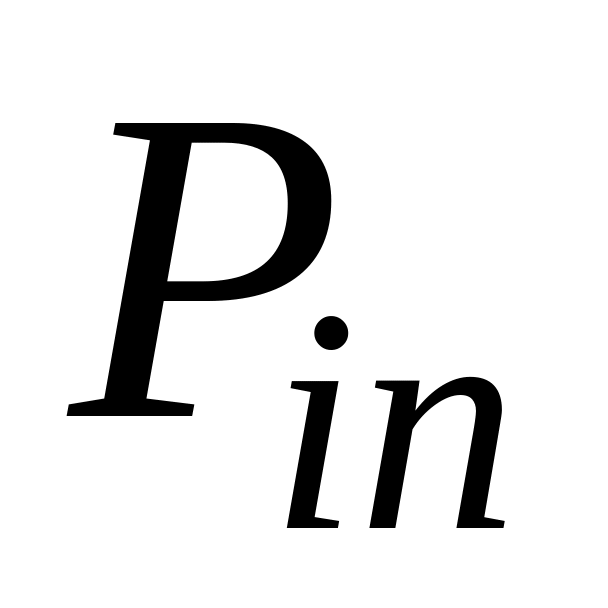
...
...
...
...
...
...
...
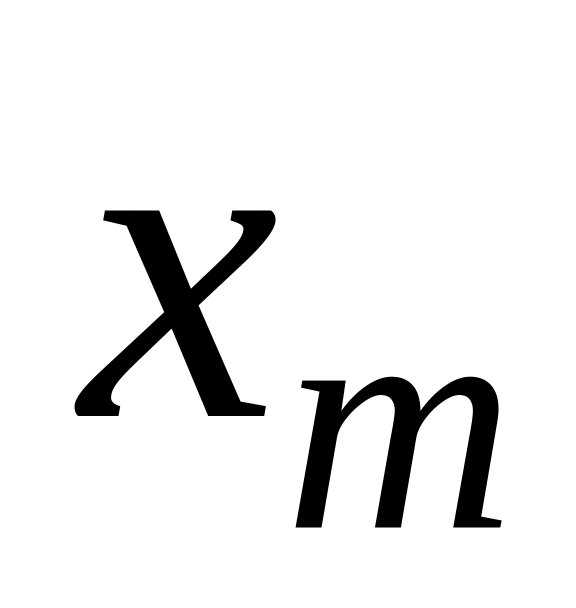
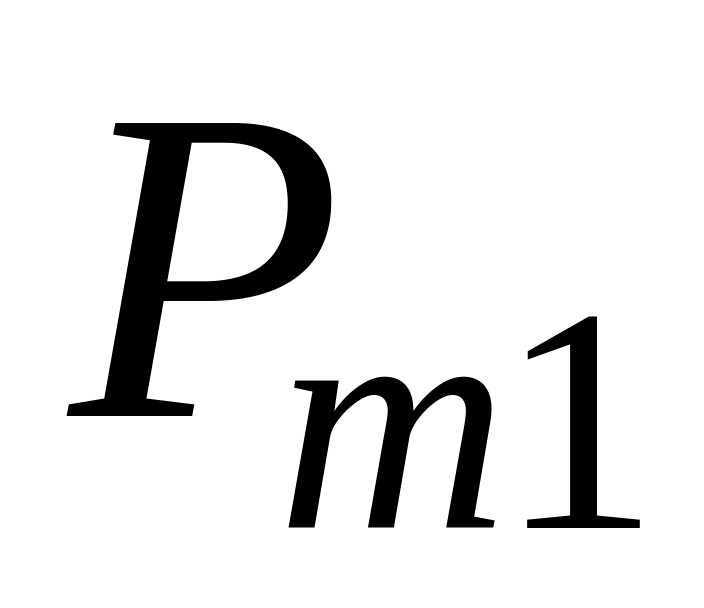
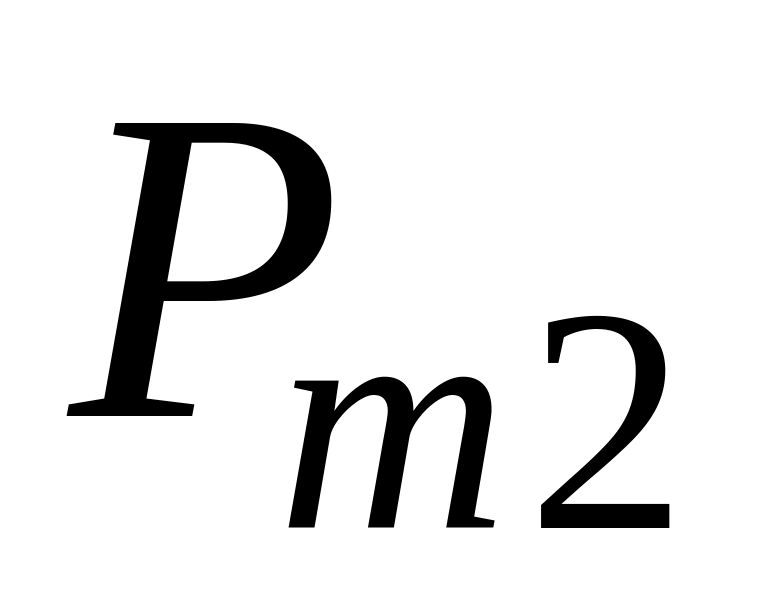
...
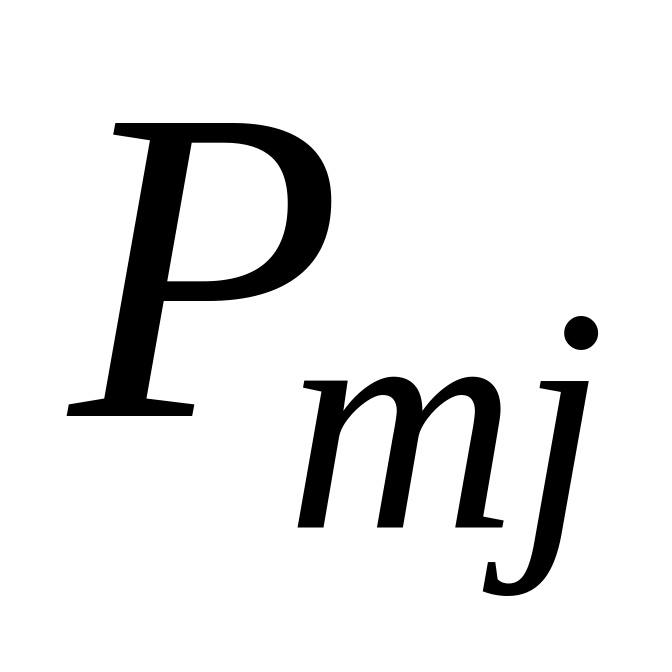
...
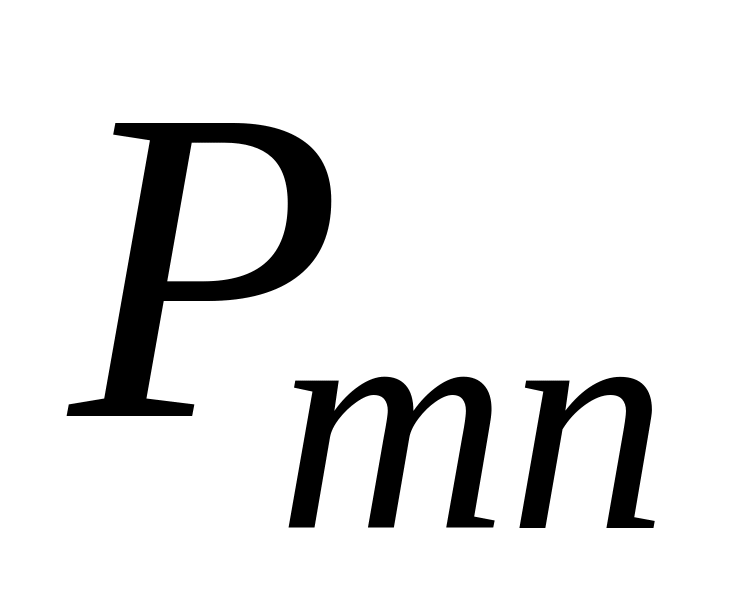
Здесь
![]()
![]() .
.
2.
Функция
распределения
системы двух случайных величин
- это вероятность совместного выполнения
двух неравенств
![]() и
и
![]() :
:
![]() .
.
Геометрически
функция
![]() есть вероятность попадания случайной
точки
в бесконечный квадрант с вершиной в
точке
есть вероятность попадания случайной
точки
в бесконечный квадрант с вершиной в
точке
![]() ,
лежащий левее и ниже значения
.
,
лежащий левее и ниже значения
.
Аналогично,
как частный случай, функция распределения
одной случайной величины
![]() есть вероятность попадания случайной
точки в полуплоскость, ограниченную
справа абсциссой x.
есть вероятность попадания случайной
точки в полуплоскость, ограниченную
справа абсциссой x.
Функция
![]() есть вероятность попадания точки
в
полуплоскость, ограниченную сверху
ординатой
есть вероятность попадания точки
в
полуплоскость, ограниченную сверху
ординатой
![]() .
.
Свойства
функции
![]() :
:
а)
есть неубывающая функция обоих своих
аргументов, т.е. при
![]()
![]() ;
при
;
при
![]()
![]() .
.
б)
![]() .
.
в)
![]() ,
т.е. при одном из аргументов, равном +¥,
функция распределения системы превращается
в функцию распределения одной СВ,
соответствующей другому аргументу.
,
т.е. при одном из аргументов, равном +¥,
функция распределения системы превращается
в функцию распределения одной СВ,
соответствующей другому аргументу.
г)
![]() .
.
д) Вероятность попадания случайной точки в прямоугольник , ограниченный абсциссами a и b и ординатами c и d, определяется через по соотношению
![]() .
.
3. Плотность распределения системы двух СВ представляет собой предел отношения вероятности попадания в малый прямоугольник к площади этого прямоугольника, когда оба его размера стремятся к нулю. Она может быть выражена как вторая смешанная частная производная функции распределения системы по обоим аргументам:
![]()
![]() .
.
Элементом
вероятности
называется выражение
![]() .
Это вероятность попадания случайной
точки
в элементарный прямоугольник со сторонами
.
Это вероятность попадания случайной
точки
в элементарный прямоугольник со сторонами
![]() ,
,
![]() ,
примыкающий к точке
.
Эта вероятность равна объему элементарного
параллелепипеда, ограниченного сверху
поверхностью
,
примыкающий к точке
.
Эта вероятность равна объему элементарного
параллелепипеда, ограниченного сверху
поверхностью
![]() и опирающегося на элементарный
прямоугольник
и опирающегося на элементарный
прямоугольник
![]() .
.
Вероятность
попадания случайной точки в произвольную
область
![]() может быть получена суммированием
(интегрированием) элементов вероятности
по всей области
:
может быть получена суммированием
(интегрированием) элементов вероятности
по всей области
:
![]() .
.
Геометрически вероятность попадания в область изображается объемом цилиндрического тела, ограниченного сверху поверхностью распределения и опирающегося на область . В частности, вероятность попадания случайной точки в прямоугольник , ограниченный абсциссами a и b и ординатами c и d, выражается зависимостью:
![]() .
.
Функция распределения выражается через функцию плотности соотношением:
![]() .
.
Основные свойства плотности распределения системы :
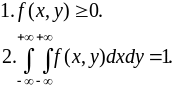
Зная закон распределения системы двух случайных величин, можно всегда определить законы распределения отдельных величин, входящих в систему (маргинальные законы распределения).
Ранее
получили:
![]() .
.
Так
как
![]() ,
то, дифференцируя последнее выражение
по x,
будем иметь:
,
то, дифференцируя последнее выражение
по x,
будем иметь:
![]() .
.
Аналогично,
![]() .
.
Зная
,
легко определяются
и
![]() .
Наоборот - труднее, так как надо знать
условные законы распределения.
.
Наоборот - труднее, так как надо знать
условные законы распределения.
Условным законом распределения величины X, входящей в систему , называется ее закон распределения, вычисленный при условии, что другая случайная величина Y приняла определенное значение y. Зная закон распределения одной из величин и условный закон распределения другой, можно составить закон распределения системы.
Теорема
умножения законов распределения:
![]() .
.
Аналогично:
![]() .
.
Условные законы распределения можно определить через безусловные:
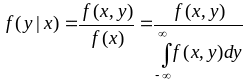 ;
;
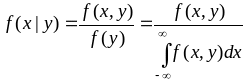 .
.
Случайная
величина
![]() называется независимой
от случайной величины
,
если закон распределения величины
не зависит от того, какое значение
приняла величина
.
называется независимой
от случайной величины
,
если закон распределения величины
не зависит от того, какое значение
приняла величина
.
Для
непрерывных случайных величин условие
независимости
от
может быть записано в виде:
![]() при
любом у.
при
любом у.
Если
зависит от
,
то
![]() .
Зависимость или независимость случайных
величин всегда взаимны: если величина
не зависит от
,
то и величина
не зависит от
.
.
Зависимость или независимость случайных
величин всегда взаимны: если величина
не зависит от
,
то и величина
не зависит от
.
Случайные величины и называются независимыми, если закон распределения каждой из них не зависит от того, какое значение приняла другая. В противном случае величины и называются зависимыми.
Для
независимых непрерывных случайных
величин теорема умножения законов
распределения принимает вид:
![]() ,
т.е. плотность распределения системы
независимых случайных величин равна
произведению плотностей распределения
отдельных величин, входящих в систему.
,
т.е. плотность распределения системы
независимых случайных величин равна
произведению плотностей распределения
отдельных величин, входящих в систему.
Это условие может рассматриваться как необходимое и достаточное условие независимости случайных величин.
Числовые характеристики системы двух случайных величин
Начальным
моментом порядка
![]() системы
называется математическое ожидание
произведения
системы
называется математическое ожидание
произведения
![]() на
на
![]() :
:
![]()
Центральным
моментом порядка
системы
называется математическое ожидание
произведения
-й
и s-й
степеней соответствующих центрированных
величин:
![]()
Для дискретных случайных величин начальные и центральные моменты вычисляются, соответственно, по формулам:
![]() ;
;
![]()
где
![]() -
вероятность того, что система
примет значения
-
вероятность того, что система
примет значения
![]() ,
а суммирование распространяется по
всем возможным значениям случайных
величин
,
.
,
а суммирование распространяется по
всем возможным значениям случайных
величин
,
.
Для непрерывных случайных величин:
![]() ;
;
![]() ,
,
где
![]() - плотность распределения системы
.
- плотность распределения системы
.
Очевидно,
что
![]() ;
;
![]() .
.
Совокупность
математических ожиданий
![]() и
и
![]() представляет собой характеристику
положения центра системы
.
Геометрически это координаты средней
точки на плоскости (центр тяжести),
вокруг которой происходит рассеяние
всех точек
.
представляет собой характеристику
положения центра системы
.
Геометрически это координаты средней
точки на плоскости (центр тяжести),
вокруг которой происходит рассеяние
всех точек
.
Дисперсии
величин Х
и Y
характеризуют рассеяние случайной
точки в направлении осей
![]() и
и
![]() :
:
![]() .
.
![]() .
.
Особую
роль как характеристики системы играет
второй смешанный центральный момент
![]() ,
т.е. математическое ожидание произведения
центрированных величин.
,
т.е. математическое ожидание произведения
центрированных величин.
Это ковариационный момент (т.е. момент связи, корреляционный момент) случайных величин , . Для дискретных случайных величин корреляционный момент выражается формулой:
![]()
а
для непрерывных
![]() .
.
Корреляционный момент есть характеристика системы случайных величин, описывающая, помимо рассеяния величин и , еще и связь между ними. Для независимых случайных величин корреляционный момент равен нулю.
Корреляционный
момент характеризует не только зависимость
величин, но и их рассеяние. Поэтому для
характеристики степени тесноты связи
между величинами
в чистом виде переходят от момента
![]() к безразмерной характеристике
к безразмерной характеристике
![]() ,
где
,
где
![]() - средние квадратические отклонения
величин
и
.
Эта характеристика называется
коэффициентом
корреляции
величин
и
.
- средние квадратические отклонения
величин
и
.
Эта характеристика называется
коэффициентом
корреляции
величин
и
.
Две независимые случайные величины всегда являются некоррелированными. Обратное верно не всегда. Равенство нулю коэффициента корреляции (корреляционного момента) есть необходимое, но недостаточное условие независимости случайных величин.
Условие независимости случайных величин - более жесткое, чем условие некоррелированности. Коэффициент корреляции характеризует степень тесноты только линейной зависимости между случайными величинами.
Свойства коэффициента корреляции:
![]() ,
где
,
где
![]() -
константы;
-
константы;
![]()
Минимальное
число характеристик, с помощью которых
может быть охарактеризована система
n
случайных величин
![]() ,
сводится к следующему: n
математических ожиданий
,
сводится к следующему: n
математических ожиданий
![]() ,
характеризующих средние значения
величин; n
дисперсий
,
характеризующих средние значения
величин; n
дисперсий
![]() ,
характеризующих их рассеяние;
,
характеризующих их рассеяние;
![]() корреляционных моментов
корреляционных моментов
![]()
![]() ,
характеризующих попарную корреляцию
всех величин, входящих в систему.
,
характеризующих попарную корреляцию
всех величин, входящих в систему.
Дисперсия
каждой из случайных величин
![]() есть частный случай корреляционного
момента, а именно, корреляционный момент
величины
и той же величины
:
есть частный случай корреляционного
момента, а именно, корреляционный момент
величины
и той же величины
:
![]() .
.
Все корреляционные моменты и дисперсии удобно располагать в виде симметричной по отношению к главной диагонали квадратной корреляционной матрицы случайных величин :
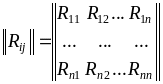 ,
где
,
где
![]() ;
;
![]()
В
целях наглядности суждения именно о
коррелированности случайных величин
безотносительно к их рассеиванию часто
пользуются нормированной корреляционной
матрицей
![]() ,
составленной из коэффициентов корреляции
,
составленной из коэффициентов корреляции
![]() ;
;
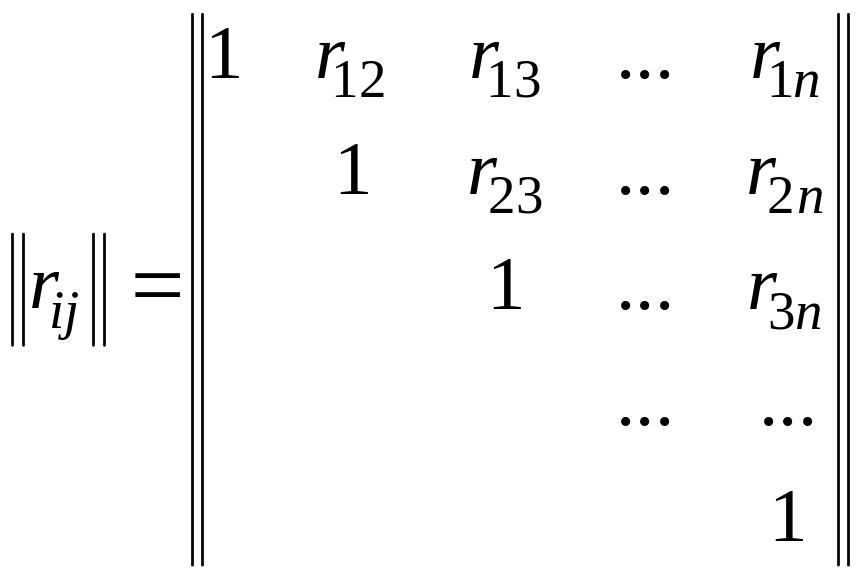 .
.
Плотность нормального распределения двух случайных величин выражается формулой:
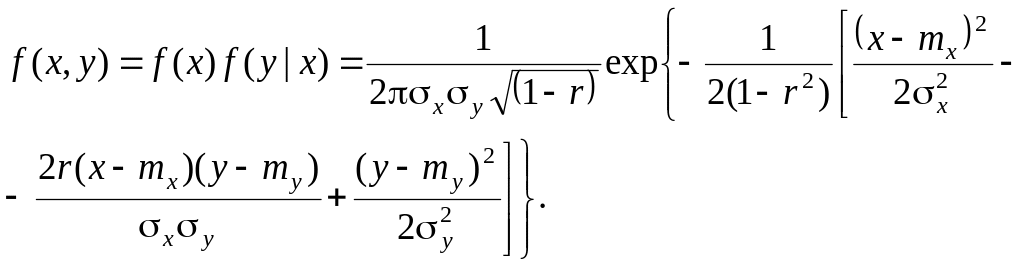
Этот
закон зависит от пяти параметров:
![]() .
.
Параметры
![]() представляют собой математические
ожидания (центры рассеивания) величин
и
;
представляют собой математические
ожидания (центры рассеивания) величин
и
;
![]() -
их средние квадратические отклонения;
- коэффициент корреляции величин
и
.
-
их средние квадратические отклонения;
- коэффициент корреляции величин
и
.
Если
и
![]() не коррелированы, то
не коррелированы, то
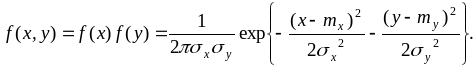
Для системы СВ, подчиненных нормальному закону, из некоррелированности величин вытекает также их независимость.
Термины "некоррелированные" и "независимые" величины для случая нормального распределения эквивалентны.
Условный закон двухмерного нормального распределения:

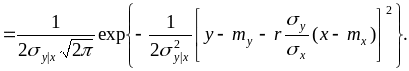
Очевидно,
что последнее выражение есть плотность
нормального закона с центром рассеяния
![]() и средним квадратическим отклонением
и средним квадратическим отклонением
![]()
Из
последних формул следует, что в условном
законе распределения величины
при фиксированном
![]() от этого значения зависит только условное
математическое ожидание
от этого значения зависит только условное
математическое ожидание
![]() ,
но не дисперсия.
,
но не дисперсия.
Прямая
![]() называется линией
регрессии
на
.
Аналогично прямая
называется линией
регрессии
на
.
Аналогично прямая
![]() есть линия регрессии
на
.
есть линия регрессии
на
.
