Распределение Фишера.
Важные приложения имеет в статистике случайная величина
,
где X – случайная величина, распределенная по закону 2 с k1 степенями свободы, а Y – случайная величина, распределенная по закону 2 с k2 степенями свободы, причём X и Y –независимые случайные величины.
Случайная величина F распределена по закону, называемому законом распределения Фишера с k1 и k2 степенями свободы. При заданных числах k1 и k2 и по вероятности q по таблице определяется значение Fq такое, что
P(F > Fq) = q.
Обычно таблицы составляются для значений q, равных 0,05 или 0,01, а иногда для обоих этих значений. Фрагмент такой таблицы представляет собой таблица 3.
-
k1
k2
1
...
10
...
20
...
1
161,4
647,8
...
241,9
6056
...
248
6209
...
...
...
...
...
...
...
...
10
4,96
10,04
...
2,97
4,85
...
2,77
4,41
...
...
...
...
...
...
...
...
Таблица 3.
В этой таблице в верхней части каждой клетки дается значение Fq при q = 0,05 , а в нижней части — при q = 0,01.
Раздел 1.4.4.Понятие случайного вектора.
Определение. Пара случайных величин (X,Y) (или (ξ,η) называется двумерной случайной величиной (двумерным случайным вектором)
Когда речь идет о двух случайных величинах, мы можем интересоваться распределением каждой из них «самой по себе», а также условным рапсределением (одной, при условии, что вторая приняла какие-то значения).
Соответствующее распределение случайного вектора называется совместным рапсределением.
(Совместная) функция распределения F(x,y)=P{X<x, Y<y} в данном случае есть вероятность попасть в квадрант , верхним правым углом которого является точка (x,y )
Определение. Две случайные величины
Х = {x1,x2,,xn}; Y = {у1, у2,,уm},
определённые на одном и том же пространстве элементарных исходов, имеющие законы распределения
-
X
х1
xi
Y
y1
yj
Р
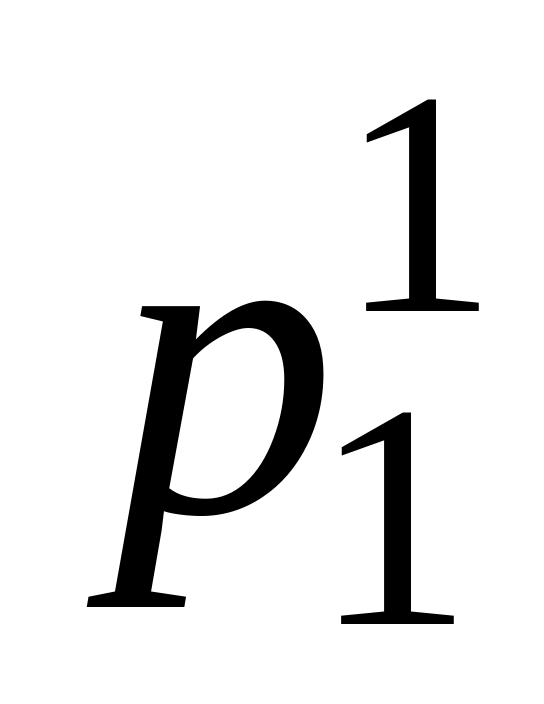
Р
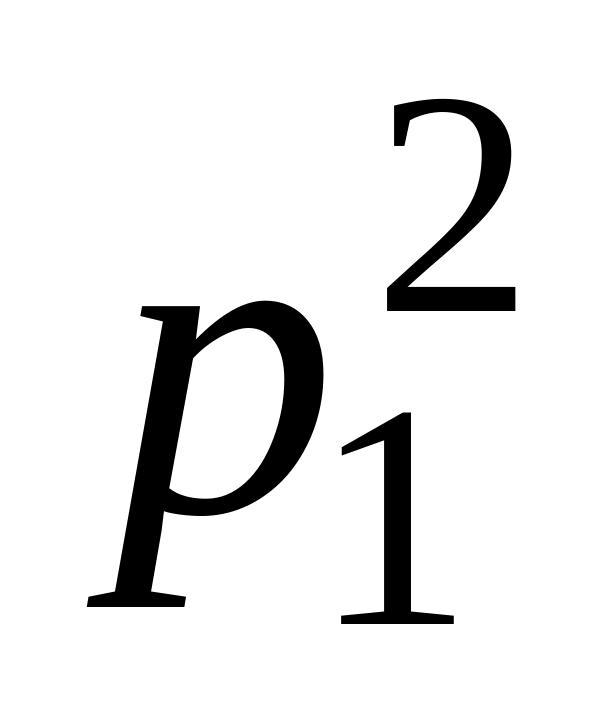
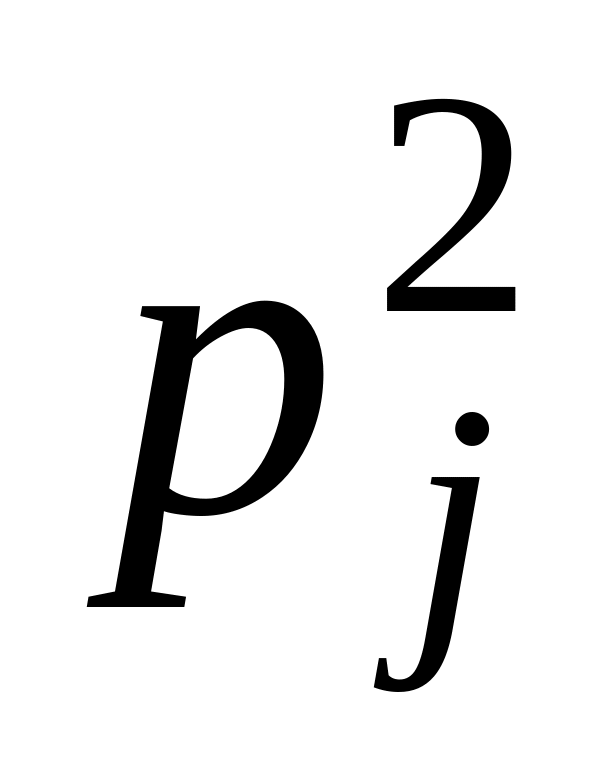
называются независимыми, если при любых i и j выполняется равенство
Р((X = хi) ∩ (Y = yj)) =
Пример1. Брошены две игральных кости. Число очков, выпавшее на первой кости, – случайная величина . Число очков, выпавшее на второй кости – случайная величина . Считаем, что все исходы ((X = i)∩(Y = j)) (i = 1,2,,6; j = 1,2, ,6) равновероятны, всего их 36, поэтому
P((X = i)∩(Y = j)) = 
Так как P(X = i) = 
и P(Y = j)) =
,
очевидно, что по определению X
и Y – независимые
случайные величины.
Пример 2. Даны две независимые случайные величины X и Y с заданными законами распределения
-
X
0
1
Y
1
2
Р
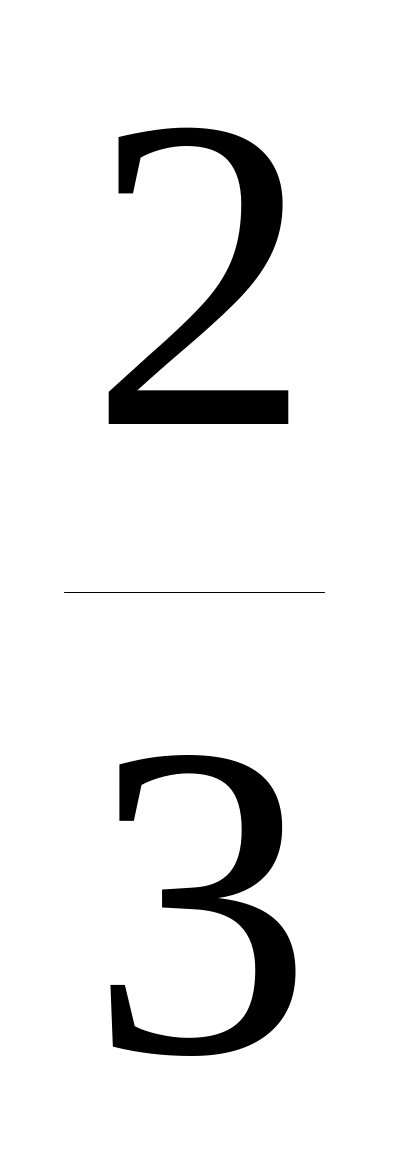
Р
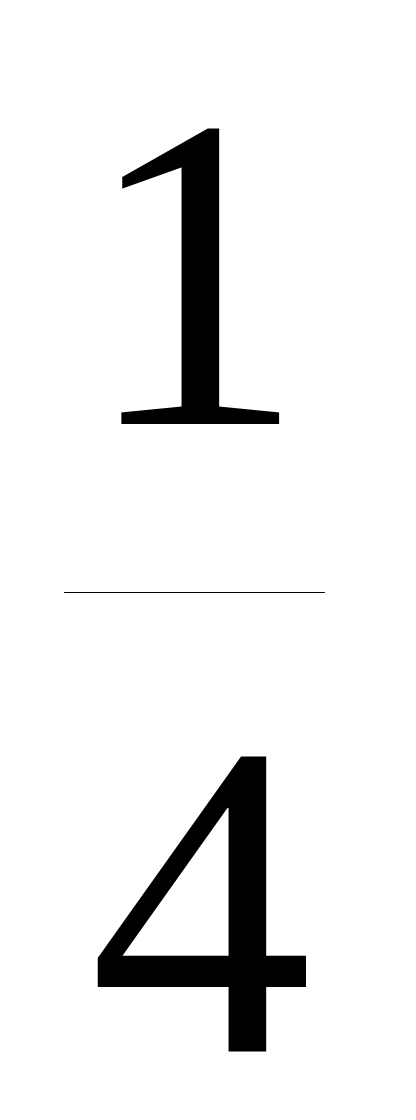
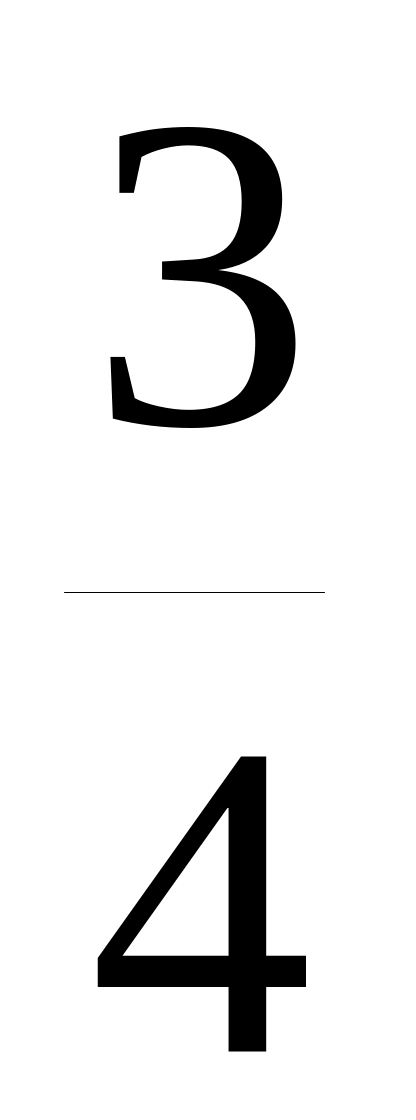
Определим случайные величины и следующим образом: = X + Y, = XY. Выясним, являются ли независимыми случайные величины и .
Составим
закон распределения .
Наименьшее значение
равняется 1. Вероятность события = 1
равна вероятности события (X = 0)∩(Y = 1),
которая в силу независимости X
и Y равна
.
Событие = 2
совпадает с событием ((X = 0)∩(Y = 2))
+ ((X = 1)∩(Y = 1)).
Его вероятность равна
.
Максимальное
значение ,
равное 3, имеет вероятность
.
Таким образом, закон распределения
случайной величины
можно представить таблицей
-
1
2
3
Р
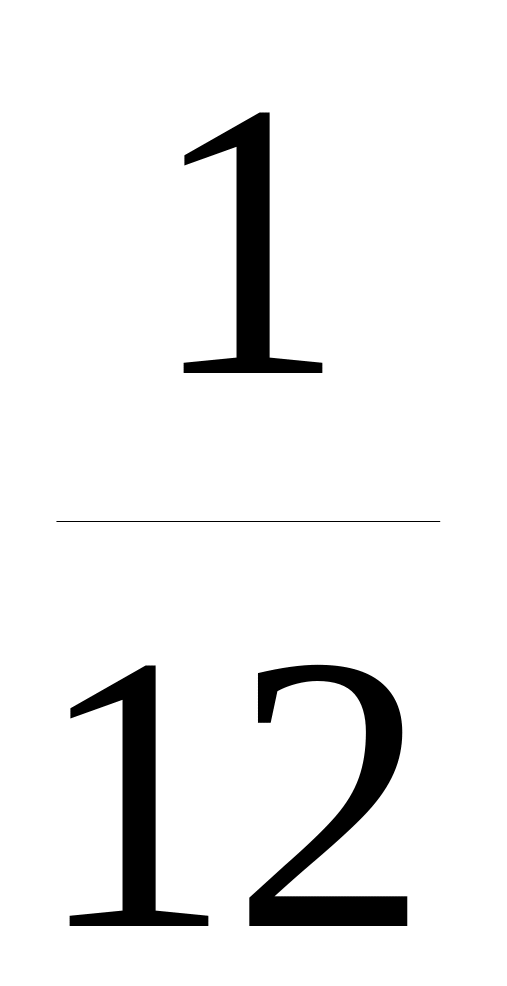
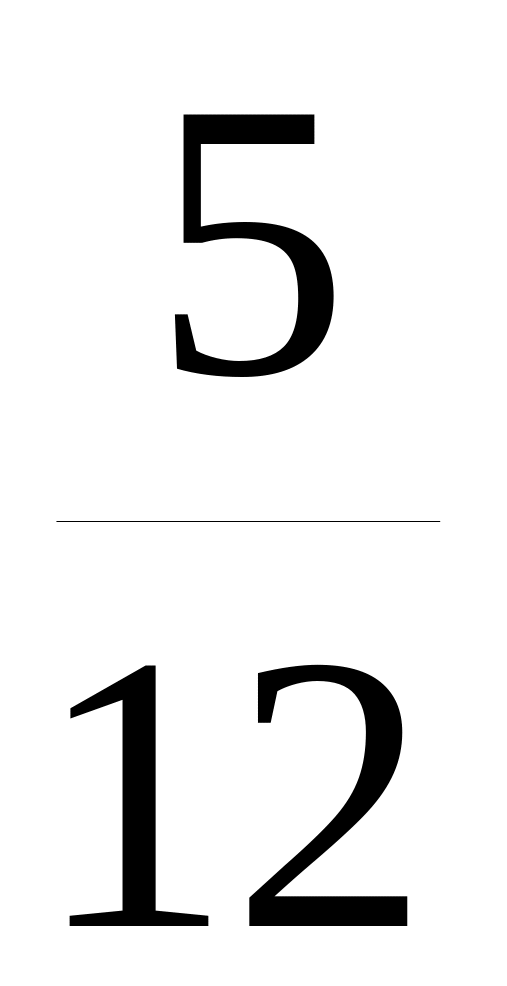
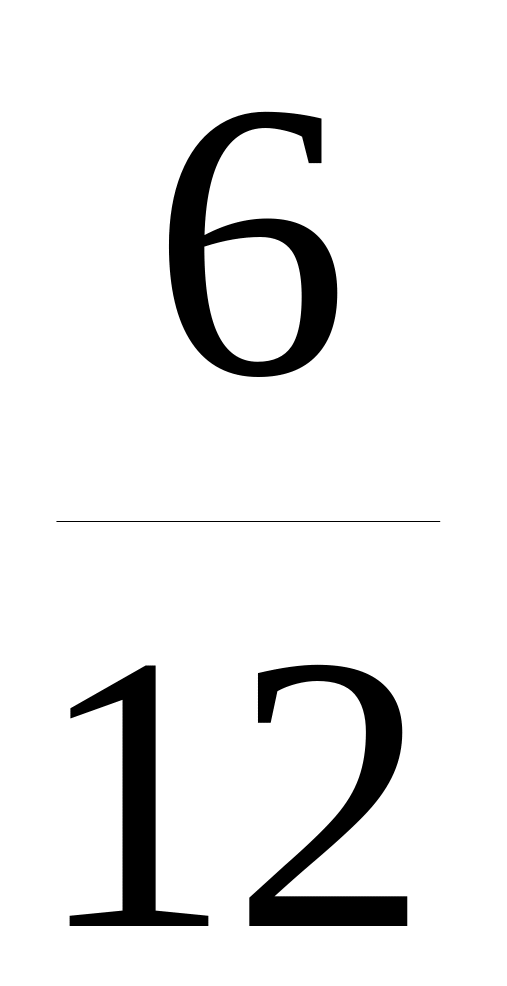
Закон распределения представляется таблицей
-
0
1
2
Р
Рассмотрим события = 3 и = 0. Очевидно, что
Р( = 3)
Р( = 0) = 
С другой стороны, событие ( = 3)∩( = 0) – невозможное, так как = 3 только при X = 1, а = 0 лишь при X = 0. Отсюда следует, что
Р(( = 3)∩( = 0)) = 0,