
- •Глава 1.1. Случайные события и их вероятности
- •Раздел 1.1.1. События Случайный эксперимент, элементарные исходы, события.
- •Раздел 1.1.2. Определения вероятности
- •Вероятностное пространство Случай конечного или счетного числа исходов.
- •Комбинаторные формулы и правила
- •Классическое определение вероятности
- •Приложение Парадокс игры в кости и Парадокс де Мере из главы 1 «Классические парадоксы теории вероятностей» книги г.Секей «Парадоксы теории вероятностей и математической статистики»
- •Статистическое определение вероятности.
- •Геометрическая вероятность
- •Раздел 1.1.3. Вероятностная модель эксперимента с бесконечным числом исходов. Аксиоматика Колмогорова
- •Приложение. Самое интересное.
- •Формулы сложения вероятностей.
- •Условные вероятности.
- •Формулы сложения вероятностей.
- •Формула полной вероятности.
- •Формула Байеса
- •Приложение. Парадокс независимости
Глава 1.1. Случайные события и их вероятности
Раздел 1.1.1. События
Случайные события. Действия над событиями. Совместные и несовместные события. Элементарные события. Противоположные события. Равновозможные события. Пространство элементарных событий
Раздел 1.1.2. Определения вероятности
Вероятностное пространство Случай конечного или счетного числа исходов. Отступление. Немного о комбинаторике
Классическое определение вероятности
Приложение. Парадокс игры в кости и парадокс де Мере
Статистическое определение вероятности
Геометрические вероятности
Раздел 1.1.3.Вероятностная модель эксперимента с бесконечным числом исходов Аксиоматика Колмогорова
Приложение. Самое интересное.
Раздел 1.1.4 Условные вероятности. Независимость событий
Независимые события. Теоремы о сложении и умножении вероятностей
Формула полной вероятности
Формула Байеса
Приложение. Парадокс независимости и другие парадоксы.
Раздел 1.1.1. События Случайный эксперимент, элементарные исходы, события.
Из книги В.Феллера «Введение в теорию вероятностей и ее приложения, т.1, гл. 1 Пространство элементарных событий»
§1. Эмпирические основания



Перейдем теперь к определениям.
Определение. Случайным (стохастическим) экспериментом или испытанием называется осуществление какого-либо комплекса условий, который можно практически или мысленно воспроизвести сколь угодно большое число раз.
Примеры случайного эксперимента: подбрасывание монеты, извлечение одной карты из перетасованной колоды, подсчет числа автомобилей в очереди на бензоколонке в данный момент.
Явления, происходящие при реализации этого комплекса условий, то есть в результате случайного эксперимента, называются элементарными событиями (исходами, элементарными исходами). Считается, что при проведении случайного эксперимента реализуется только одно из возможных элементарных событий.
Если монету подбросить один раз, то элементарными исходами можно считать выпадение герба (Г) или решетки (числа) (Р).
Если случайным экспериментом считать троекратное подбрасывание монеты, то элементарными исходами можно считать следующие:
ГГГ, ГГР, ГРГ, РГГ, ГРР, РГР, РРГ, РРР.
Множество всех элементарных исходов случайного эксперимента называется пространством элементарных событий (ПЭС) (исходов). Будем обозначать пространство элементарных исходов греческой буквой (омега большая) i-й элементарный исход будем обозначатьi (-омега малая).
Если пространство элементарных исходов содержит n элементарных исходов, то = (1, 2 ,..., n ).
Если монета подбрасывается 1 раз, = {Г, Р} Для троекратного подбрасывания монеты, ={ГГГ, ГГР,..., РРР}. Здесь точки пространства Ω – тройки значков Г или Р.
Если случайный эксперимент - подбрасывание игральной кости, то ={1,2,3,4,5,6}, двукратное - ={(1,1) (1,2) …(6,6)}, здесь точками являются пары чисел.
Замечание. Очевидно, что если в одном опыте исходов только 2, количество точек в пространстве элементарных событий #Ω = 2n, где n – число опытов в серии (согласно комбинаторному правилу произведения )
Там же, §3 «Пространство элементарных событий»:

Случайным событием (или просто событием) называется подмножество множества (пространства) .
С точки зрения числа элементов, образующих множество, оно может быть конечным или бесконечным. Бесконечное множество в совю очередь может быть счетным или несчетным.
Множество называется счетным, если между ним и множеством N натуральных чисел можно установить взаимно-однозначное соответствие (биекцию) (т.е., существует возможность занумеровать все элементы множества, не повторившись и никакие не пропустив)
Пример счетного множества: множество натуральных, целых, рациональных чисел.
Множество называется несчетным (имеет мощность континуума), если при любом способе нумерации останутся незанумерованные элементы (то есть, установление взаимно-однозначного соответствия с множеством натуральных чисел невозможно). Примеры несчетных множеств: множество точек на заданном отрезке, множество чисел x, удовлетворяющих неравенству a< x <b, множество действительных чисел.
Приведем примеры событий. Пусть бросается игральная кость, и элементарным исходом считается выпавшее число очков: =(1,2,3,4,5,6). A — событие, заключающееся в том, что выпало четное число очков: А=(2,4,6); B — событие, заключающееся в том, что выпало число очков, не меньшее 3-х: B=(3,4,5,6).
Говорят, что те исходы, из которых состоит событие А, благоприятствуют событию А. Иными словами, это те исходы (точки), которые это событие (множество) образуют.
Пусть отрезок АВ поделен на отрезки и на него случайным образом бросается точка. Тогда событием будет попадание точки в некоторый маленький отрезок.
Таким образом, увидев, что события можно рассматривать как множества (исходов), мы смело можем применить к ним аппарат теории множеств.
Напоминание. Множеством называется совокупность объектов, «собранных» вместе по какому-то принципу. Основным вопросом здесь является не природа этих объектов (называемых элементами или точками), а их принадлежность или непринадлежность данному множеству.
Замечание. Рассматривая множества (события) и действия над ними, обычно имеют в виду существование некоторого основного (базового) множества, из которого черпают примеры множеств. Мы будем обозначать его Ω (это определенное выше пространство элементарных событий). В теории множеств его обозначают какой-либо заглавной латинской буквой, например М.
Отступление. Действия над множествами (событиями)
Рис.1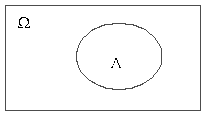
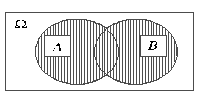
![]() или
А+В)
называется событие, состоящее из всех
элементарных исходов, принадлежащих
по крайней мере одному из событий А
или B.
Событие AUB
происходит, если происходит по крайней
мере одно из событий А
или B.
или
А+В)
называется событие, состоящее из всех
элементарных исходов, принадлежащих
по крайней мере одному из событий А
или B.
Событие AUB
происходит, если происходит по крайней
мере одно из событий А
или B.
Рис.2
Рис.3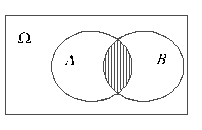
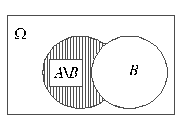
Рис.4
Симметрической разностью А∆В называется событие, состоящее из всех исходов, входящих в события А и В по-отдельности, но не принадлежащие им обоим (на рис. 3 – незаштрихованная область внутри А и В). А∆В = AUB \ A∩B
В условиях упомянутого примера это означает, что попал в мишень или только первый стрелок, или только второй. Одновременно они оба в мишень не попадали.
Определения.
Событие , состоящее из всех элементарных событий (исходов) данного эксперимента, называется достоверным (оно обязательно происходит в результате случайного эксперимента).
Пустое множество , не содержащее ни одного элемента (исхода), называется невозможным событием.
Событие
![]() =\A
=
СΩ
А, состоящее из всех исходов, не
принадлежащих событию А (но принадлежащих
определенному пространству элементарных
событий Ω) называется
противоположным
событию
А
или дополнением
события
А
(до
множества (пространства) Ω).
=\A
=
СΩ
А, состоящее из всех исходов, не
принадлежащих событию А (но принадлежащих
определенному пространству элементарных
событий Ω) называется
противоположным
событию
А
или дополнением
события
А
(до
множества (пространства) Ω).
Замечание. Существенно, что мы находимся все время в рамках одного и того же основного множества – Ω, поскольку без него операцию дополнения просто не определить.
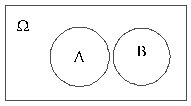
События А и B называются несовместными, если нет исходов, принадлежащих и А и B, то есть A∩B = . На рисунке 5 изображены несовместные события А и B.
Рис.5
Непосредственно
из введенных определений следуют
равенства: AU![]() =;
A∩
=;
A∩![]() =;
=;
![]() ∩
∩![]() ;
;
![]() =
=![]() .
Два последних равенства называются
формулами Де'Моргана.
.
Два последних равенства называются
формулами Де'Моргана.
Пример 1. Подбрасываются два игральных кубика, подсчитываются
суммы выпавших очков (суммы числа очков на верхних гранях обоих
кубиков). Сумма выпавших очков на двух кубиках может меняться от 2
до 12. Описать пространство элементарных событий в этом опыте.
Реш е н и е. Полную группу событий образуют равновозможные элементарные
исходы (k; m), k, m = 1,2, 3, 4, 5, 6, представленные в таблице
1.1. Элементарный исход (k; m) означает, что на первом кубике выпало
k очков, на втором m очков (k, m = 1,2,3,4,5,6). Например, (3; 4) -
на первом кубике 3 очка, на втором - 4 очка.
Таблица 1.1.
(1; 1) (2;1) (3;1) (4;1) (5; 1) (6;1)
(1 ;2) (2;2) (3;2) (4;2) (5;2) (6;2)
(1 ;3) (2;3) (3;3) (4;3) (5;3) (6;3)
(1;4) (2;4) (3;4) (4;4) (5;4) (6;4)
(1;5) (2;5) (3;5) (4;5) (5;5) (6;5)
(1;6) (2;6) (3;6) (4;6) (5;6) (6;6)
Пример 2. Сколько элементарных исходов благоприятствует событию
"на обоих кубиках выпало одинаковое число очков" при подбрасывании
двух игральных кубиков?
Решение. Этому событию благоприятствуют 6 элементарных исходов
(см. табл. 1.1): (1;1), (2;2), (3;3), (4;4), (5;5), (6;6).
Пример 3. Подбрасывается два игральных .кубика. Какому событию
благоприятствует больше элементарных исходов: "сумма выпавших оч-
ков равна 7", "сумма выпавших очков равна 8"? .
Решение. Событию «сумма выпавших очков равна 7» благоприятствуют
6 исходов (см. табл. 1.1): (1;6), (2;5), (3;4), (4;3), (5;2), (6;1). Событию"
"сумма выпавших очков равна 8" благоприятствуют 5 исходов:
(2;6), (3;5), (4;4), (5;3), (6;2). Следовательно, первому событию благоприятствует больше элементарных исходов.
Пример 4. Подбрасываются три игральных кубика, подсчитываются
суммы очков, выпавших на них. Сколькими способами можно получить
в сумме 5 очков, 6 очков?
Решение. Получить в сумме 5 очков можно шестью способами:
(1;1;3), (1;3;1), (3;1;1), (1;2;2), (2;1;2), (2;2;1). Получить в сумме 6 очков
можно десятью способами: (1; 1 ;4), (1 ;4; 1), (4; 1; 1), (1 ;2;3), (1 ;3;2), (2; 1 ;3),
(2;3;1), (3;1;2), (3;2;1), (2;2;2).
З а м е ч а н и е. Запись (3 ;2; 1) означает, что на первом кубике выпало 3 очка, на втором - ,2, на третьем - 1.
