Классическое определение вероятности

Вероятность события характеризует возможность (шанс) осуществления события в ходе случайного эксперимента. Смысл вероятности раскрывается в следующих требованиях, налагаемых на вероятности событий. Вероятность события выражается долей от целого, то есть является числом от нуля до единицы. При этом за единицу принимается вероятность наступления достоверного события , то есть события, которое обязательно происходит в ходе эксперимента. Вероятности невозможных событий считаются равными нулю. Если зять произвольный конечный или счетный набор событий, таких, что никакие два из них не могут произойти одновременно, то вероятность наступления хотя бы одного из этих событий должна быть равна сумме вероятностей этих событий. Иначе говоря,

Каждому элементарному исходу _i пространства  соответствует некоторая неотрицательная числовая характеристика P_i шансов его появления, называемая вероятностью исхода  _i , причем

(здесь суммирование ведется по всем i, для которых выполняется условие:  _i).

Отсюда следует, что 0  P_i  1для всех i.

Вероятность события А определяется как сумма вероятностей всех элементарных исходов, благоприятствующих событию А. Обозначим ее Р(А).

(*)

Отсюда следует, что

1) 0  P(A)  1;

2) P()=1;

3) P()=0.

Шанс наступления суммы попарно несовместных событий равен сумме шансов каждого из событий. Указанные требования налагают жесткие ограничения на численные значения вероятностей.

Вычисление значений вероятностей событий в различных случайных экспериментах является предметом теории вероятностей. Для конкретного случайного эксперимента вероятность конкретного события – объективно существующая величина. Оказывается, что численное значение той величины проявляется следующим образом. Если случайный эксперимент многократно повторить при одних и тех же условиях и вычислить частоту появлений конкретного события среди всех проведенных экспериментов (частота появления события есть отношение числа появления события к числу экспериментов) , то при неограниченном возрастании числа экспериментов эта частота в пределе совпадает вероятностью события. Рассмотрим сначала простейший случай, когда случайный эксперимент имеет конечное число исходов. Более того, каждый исход эксперимента имеет равные шансы на реализацию. Подобная ситуация называется классической схемой. Итак, пространство элементарных исходов состоит из конечного числа N элементарных исходов, причем случайный эксперимент таков, что вероятности осуществления каждого из этих N элементарных исходов представляются равными. Примеры таких случайных экспериментов: подбрасывание симметричной монеты, бросание правильной игральной кости, случайное извлечение игральной карты из перетасованной колоды. В силу введенной аксиомы вероятности каждого элементарного исхода в этом случае равны . Из этого следует, что если событие А содержит N_A элементарных исходов, то вероятность события определяется как отношение числа благоприятных исходов к общему числу всех возможных исходов.

При м е р 1. В урне 10 одинаковых по размерам и весу шаров, из которых 4 красных и 6 голубых. из урны извлекается один шар. Какова

вероятность того, что извлеченный шар окажется голубым?

Реш е н и е. Событие "извлеченный шар оказался голубым" обозначим

буквой А. Данное испытание имеет 10 равновозможных элементарных

исходов, из которых 6 благоприятствуют событию А. В соответствии с

формулой классического определения

Р(А) = 6/10 = 0,6.

При м е р 2. Все натуральные числа от 1 до 30 записаны на одинаковых

карточках и помещены в урну. После тщательного перемешивания

карточек из урны извлекается одна карточка. Какова вероятность того,

что число на взятой карточке окажется кратным 5?

Реш е н и е. Обозначим через А событие "число на взятой карточке

кратно 5". В данном испытании имеется 30 равновозможных элементарных исходов, из которых событию А благоприятствуют 6 исходов (числа 5, 1 О, 15, 20, 25, 30). Следовательно,

Р(А)= 6/30 = 1/5 = 0,2.

При м е р 3. Подбрасываются два игральных кубика, подсчитывается

сумма очков на верхних гранях. Найти вероятность события В, состоящего в том, что на верхних гранях кубиков в сумме будет 9 очков.

Реш е н и е. В этом испытании всего 6² = 36 равновозможных элементарных событий. Событию В благоприятствуют 4 исхода:

(3;6), (4;5), (5;4), (6;3), поэтому

Р(В) = 4/36 = 1/9

При м е р 4. Подбрасываются две симметричные монеты. Чему равна

вероятность того, что на верхних сторонах обеих монет оказались цифры?

Реш е н и е. Обозначим буквой D событие "на верхней стороне каждой

монеты оказалась цифра". В этом испытании 4 равновозможных

элементарных исходов: (Г, Г), (Г, Р), (Р, Г), (Р,Р). (Запись (Г, Р) означает,

что на первой монете герб, на второй – «решетка» (цифра ). Событию D благоприятствует один элементарный исход (Р, Р). Поскольку N_A = 1, N = 4 , то P(D)=1/4 =0,25.

Пример 5. Из набора, содержащего 10 одинаковых на вид электроламп, среди которых 4 бракованных, случайным образом выбирается 5 ламп. Какова вероятность, что среди выбранных ламп будут 2 бракованные (событие Е) ?

Здесь элементарным событием является выбор пяти ламп из 10 возможных. Выбор любой пятерки ламп имеет одну и ту же вероятность.

Очевидно, что порядок следования ламп в пятерке нам неважен, существенно лишь, сколько из них являются работаюими, а сколько – бракованными. Поэтому для подсчета мы выбираем подсчет сочетаний, то есть неупорядоченных наборов. Всего существует способов составить такую пятерку, то есть случайный эксперимент в данном случае имеет N = равновероятных исходов.

Сколько из этих исходов удовлетворяют условию "в пятерке две бракованные лампы", то есть сколько исходов принадлежат интересующему нас событию?

Каждую интересующую нас пятерку можно составить так: выбрать две бракованные лампы, что можно сделать числом способов, равным . Каждая пара бракованных ламп может встретиться столько раз, сколькими способами ее можно дополнить тремя не бракованными лампами, то есть раз. Получается, что число пятерок, содержащих две бракованные лампы, согласно правилу произведения, равно  .

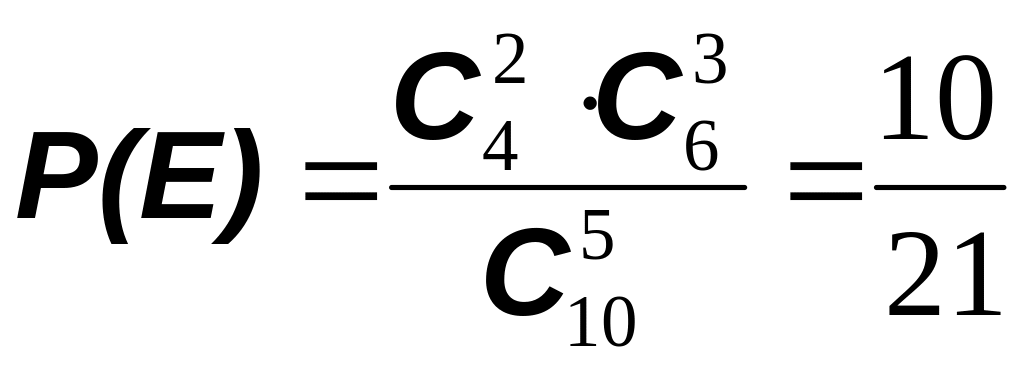
Пример 6. Кодовый замок содержит 10 цифр от 0 до 9. Замок открывается, если одна за другой последовательно нажимаются 3 разных цифры. Некто случайным образом набирает ко. Какова вероятность того, что дверь откроется (событие F)?

Здесь элементарным событием будет набор некоторого трехзначного кода, порядок цифр в котором, естественно, важен, поэтому для подсчета мы будем использовать упорядоченные наборы – размещения. Всего различных трехзначных кодов из 10 цифр можно образовать вариантов и вероятность того, что код угадан (а есть только одна правильная комбинация) составляет

P (F) =