Примеры дискретных распределений

Равномерное распределение

Дискретная величина принимает конечное число значений с одинаковыми вероятностями. Например, случайная величина принимает значение числа на верхней грани кубика при однократном подбрасывании

Х	х1	х2	х3		хn
P				

Биномиальное распределение

Случайная величина принимает значение числа успехов в схеме Бернулли из n испытаний .p – вероятность успеха q – вероятность неудачи в одном испытании, 0<p,q<1, p+q=1

P{X =i} =

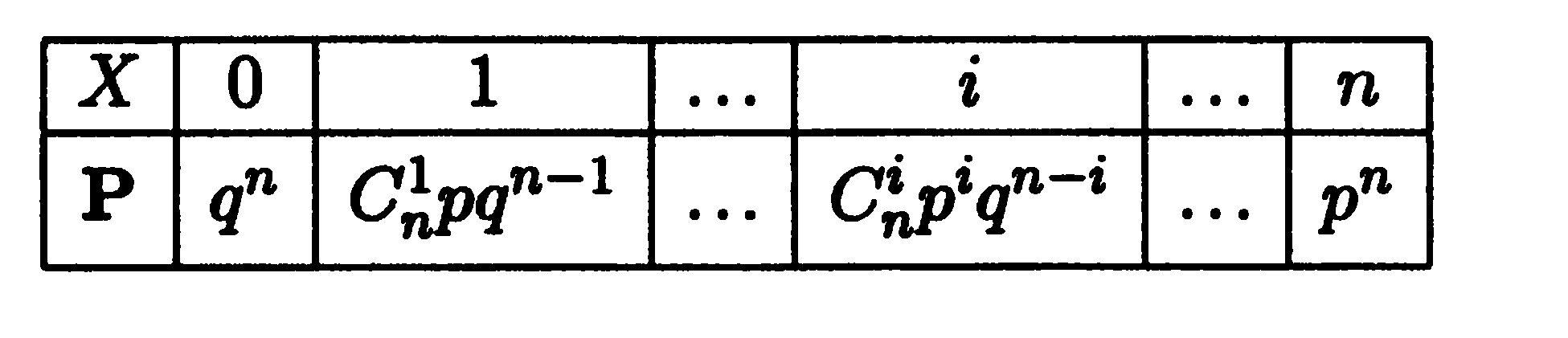
Сумма в нижней строке есть биномиальное разложение для (p+q)ⁿ =

Отступление. О Биноме Ньютона

Бином Ньютона – это формула возведения суммы в степень с натуральным показателем.

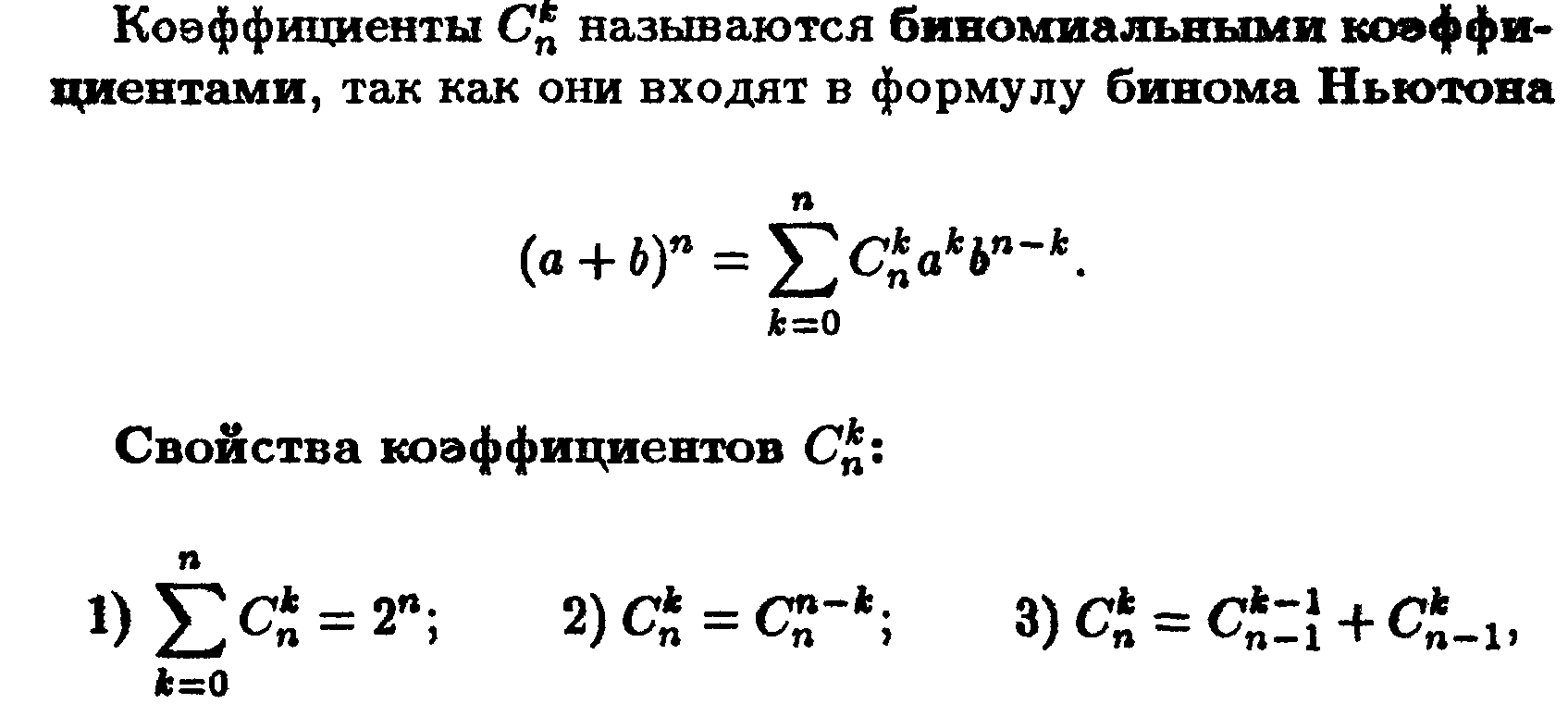
Геометрическое распределение

Случайная величина принимает значение числа неудач до первого успеха в в схеме Бернулли, p – вероятность успеха q – вероятность неудачи в одном испытании, 0<p,q<1, p+q=1. Испытания независимы, поэтому по правилу умножения вероятностей

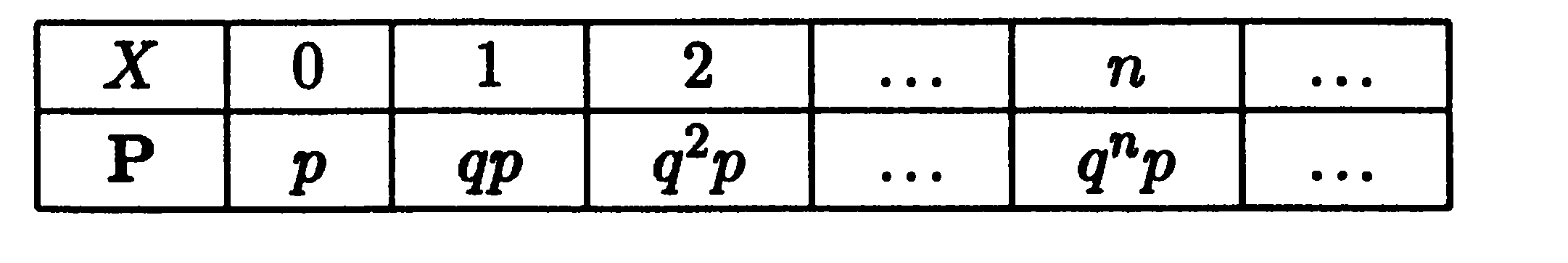
, как сумма бесконечно убывающей геометрической прогрессии

Распределение Пуассона

Случайная величина принимает значение числа успехов в схеме Бернулли из n испытаний: Х=0,1,2,…,n…, p – вероятность успеха, успехи редки, их вероятность мала. n∙p=λ>0 – параметр распределения

- сумма ряда Тейлора для экспоненты

Раздел 1.4.3. Понятие случайной величины с абсолютно непрерывным законом распределения

Определение. Случайная величина, принимающая несчетное число значений (значения которой заполняют некоторый промежуток) и имеющая плотность, называется случайной величиной с абсолютно непрерывным законом распределения или (абсолютно) непрерывной случайной величиной..

В частных случаях это может быть не один промежуток, а объединение нескольких промежутков. Промежутки могут быть конечными, полу­бесконечными или бесконечными, например: (a; b], (– ; a), [b;), (–; ).

Вообще говоря, непрерывная случайная величина – это абстракция. Снаряд, выпущенный из пушки, может пролететь любое расстояние, скажем, от 5 до 5,3 километров, но никому не придёт в голову измерять эту величину с точностью до 0,0000001 километра (то есть до миллиметра), не говоря уже об абсолютной точности. В практике такое расстояние будет дискретной случайной величиной, у которой одно значение от другого отличается по крайней мере на 1 метр.

При описании непрерывной случайной величины принципиально невозможно выписать и занумеровать все её значения, принадлежащие даже достаточно узкому интервалу. Эти значения образуют несчётное множество, называемое «континуум».

Замечание. Вернемся к нашей аналогии со стержнем. Теперь на нем не точечные массы, а сам он представляет собой стержень переменной плотности, протянувшийся от наименьшего до наибольшего значения случайной величины. Очевидно, что вопрос о массе в конкретной точке теперь невозможно поставить, а можно лишь говорить о массе, распределенной в некотором объеме (на некотором участке нашего стержня).

Таким образом, вместо вероятности-массы мы получаем плотность (вероятности). Из-за схожести физической и вероятностной плотности последнюю чаще всего обозначают, как в физике, буквой ρ (греческая ро). Другой распространенный вариант – р – подчеркивает связь с вероятностью.

Замечание. Если Х – непрерывная случайная величина, то равенство Х = х представляет собой, как и в случае дискретной случайной величины, некоторое случайное событие, но для непрерывной случайной величины это событие можно связать лишь с вероятностью, равной нулю, что однако не влечёт за собой невозможности события. Так например, можно говорить, что только с вероятностью «нуль» снаряд пролетит 5245,7183 метра, или что отклонение действительного размера детали от номинального составит 0,001059 миллиметра. В этих случаях практически невозможно установить, произошло событие или нет, так как измерения величин проводятся с ограниченной точностью, и в качестве результата измерения можно фактически указать лишь границы более или менее узкого интервала, внутри которого находится измеренное значение.

Значениям непрерывной случайной величины присуща некоторая неопределенность. Например, нет практического смысла различать два отклонения от номинального размера, равные 0,5 мм и 0,5000025 мм. Вероятность, отличная от нуля, может быть связана только с попаданием величины в заданный, хотя бы и весьма узкий, интервал. Здесь можно привести сравнение с распределением массы вдоль стержня. Отсутствует масса, сосредоточенная, скажем, в сечении, расположенном на расстоянии 20 см от левого конца стержня, имеет смысл говорить лишь о массе, заключённой между сечениями, проходящими через концы некоторого промежутка.

Пусть Х – непрерывная случайная величина. Рассмотрим для некоторого числа х вероятность неравенства х < Х < х + х

P(х < Х < х + х).

Здесь х – величина малого интервала.

Очевидно, что если х  0, то P(х < Х < х + х)  0. Обозначим (х) предел отношения P(х < Х < х + х) к при х  0, если такой предел существует:

(1)

Функция (х) называется плотностью распределения случайной величины. Из формулы (1) следует равенство, справедливое для малых величин х, которое также можно считать определением функции (х):

P(х < Х < х + х)   (x)х (2)

Очевидно, что (x) – неотрицательная функция. Для определения вероятности того, что случайная величина Х примет значение из промежутка [a, b] конечной длины, нужно выбрать на промежутке произвольные числа x₁, х₂,,  х_n удовлетворяющие условию а=х₀<х₁<x₂<<x_n<b=x_n+1. Эти числа разобьют промежуток [a, b] на n+1 частей, представляющих собой промежутки [х₀, х₁), [х₁, х₂), ,[х_n, b]. Введём обозначения:

х₀= х₁ – х₀, х₁= х₂ – х₁, , х_n = b – х_n,

и составим сумму . Рассмотрим процесс, при котором число точек разбиения неограниченно возрастает таким образом, что максимальная величина х_i стремится к нулю. Будем считать функцию  (x) непрерывной на промежутке (а; b), тогда пределом суммы будет определённый интеграл по промежутку [a; b] от функции p(x), равный искомой вероятности:

P(a  Х  b) =  (3)

З

Рис. 1

амечание. Это равенство можно также рассматривать как определение функции  (х). Отсюда следует, что вероятность попадания случайной величины в любой интервал (х₁, х₂) равна площади фигуры, образованной отрезком [х₁, х₂] оси х, графиком функции (х) и вертикальными прямыми х = х₁, х = х₂, как изображено на рисунке 1.

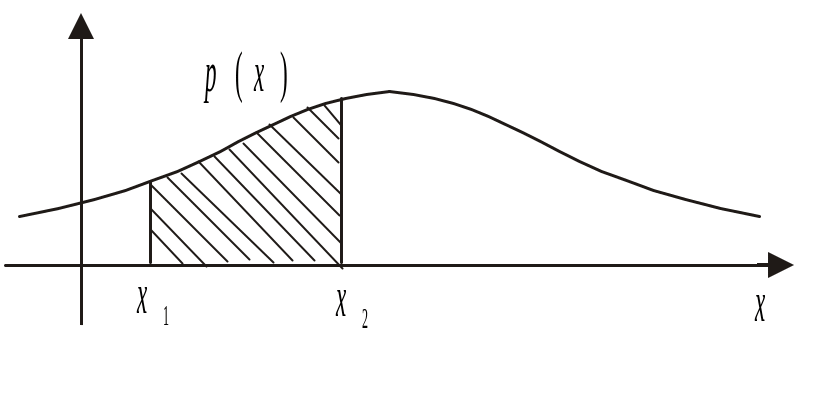
Замечание. С другой стороны, вероятность попасть в промежуток есть разность значений функции распределения на концах промежутка.

Если все возможные значения случайной величины принадлежат интервалу (а; b), то для  (х) – её плотности распре­деления справедливо равенство

Для удобства иногда считают функцию (х) определённой для всех значений х, полагая её равной нулю в тех точках х, которые не являются возможными значениями этой случайной величины.

Плотностью распределения может служить любая интегрируемая функция (х), удовлетворяющая двум условиям:

1. (х)  0;

2. 

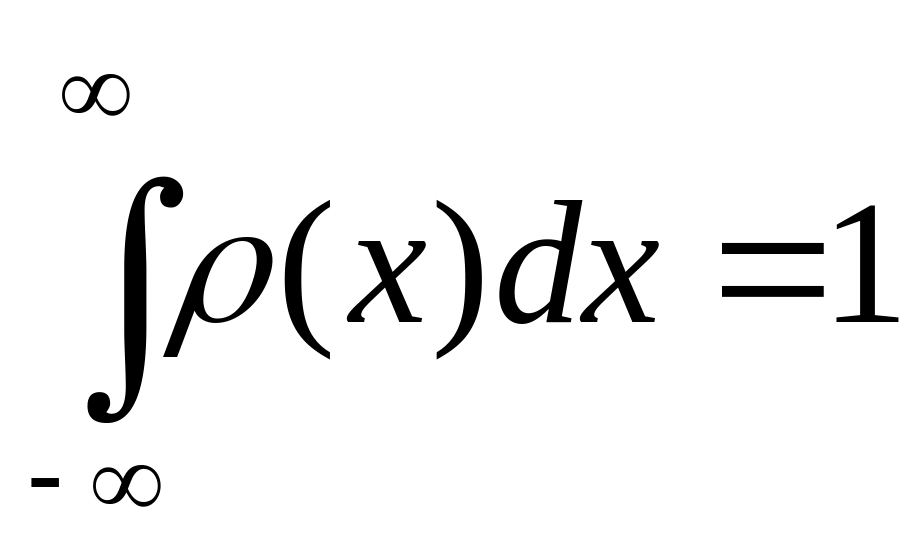
Определение. Законом распределения непрерывной случайной величины является ее плотность.

Можно задавать случайную величину, задавая функцию (х), удовлетворяющую этим условиям.

В качестве примера рассмотрим случайную величину Х, равномерно распределённую на промежутке [a; b]. В этом случае (х) постоянна внутри этого промежутка:

По свойству 2) функции  (х)

О

Рис. 2

тсюда . График функции

 (х) представлен на рисунке 2.

Замечанание. Во многих практических задачах встречаются случайные величины, у которых возможные значения не ограничены сверху и снизу. В этом случае кривая распределения располагается над осью х и при х   и х  –  асимптотически приближается к этой оси, как изображено на рисунке 1. Вероятность того, что случайная величина Х примет значение, меньшее некоторого числа а, равна площади фигуры, заключённой между кривой распределения и горизонтальной координатной осью слева от точки а. Будем считать, что такая площадь существует.

Напоминание. Пусть Х – непрерывная случайная величина. Функция F(x), которая определяется равенством

,

называется интегральной функцией распределения или просто функцией распределения случайной величины Х. Непосредственно из определения следует равенство . Формула производной определённого интеграла по верхнему пределу в данном случае приводит к соотношению . Плотность распределения  (х) называют еще дифференциальной функцией распределения.

Замечание. То обстоятельство, что производная от интеграла с переменным верхним пределом есть подинтегральная функция, является одним из ключевых в математическом анализе. Это свойство интеграла с переменным верхним пределом является связующим звеном между дифференциальным и интегральным исчислением.

Функция распределения F(x) случайной величины Х имеет следующие свойства.

1. F(x) — непрерывная возрастающая функция.

2. ;

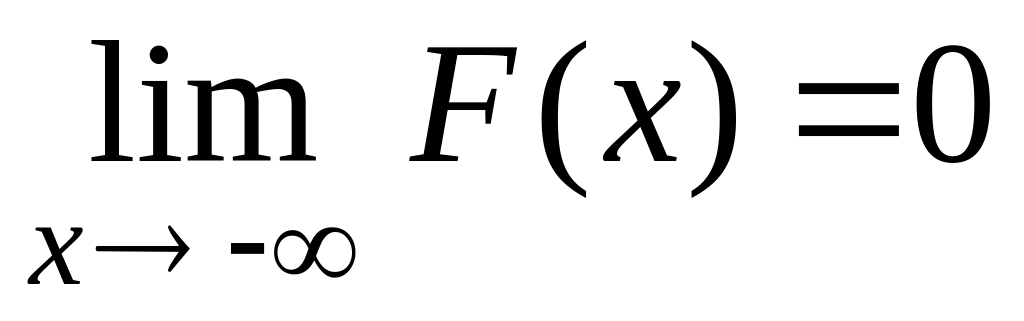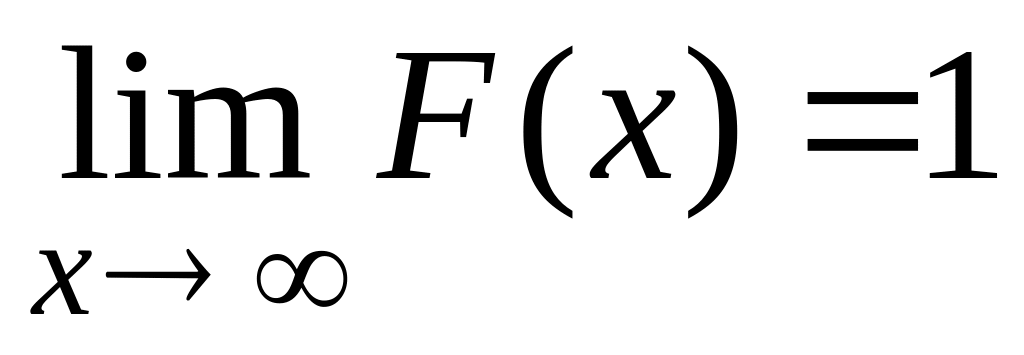
Свойства 1 и 2 вытекают непосредственно из определения функции F(x).

3. Приращение F(x) на промежутке (х₁; х₂) равно вероятности того, что случайная величина Х принимает значение из этого промежутка:

F(x₂) – F(x₁) = P(x₁ Х < x₂)

Доказательство.

F(x₂) = P(Х < x₂) = P(Х < x₁) + P(x₁  Х < x₂) = F(x₁) + P(x₁ Х < x₂)

Отсюда

P(x₁  Х < x₂) = F(x₂) – F(x₁)

Для равномерного распределения функция F(x) имеет вид:

Рис. 3

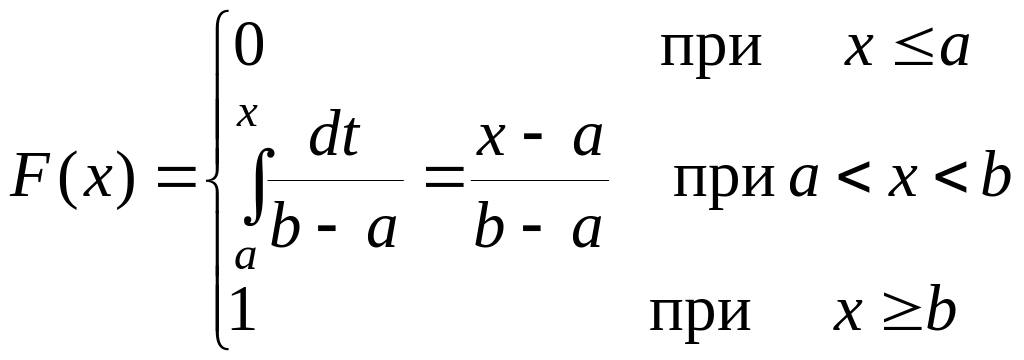
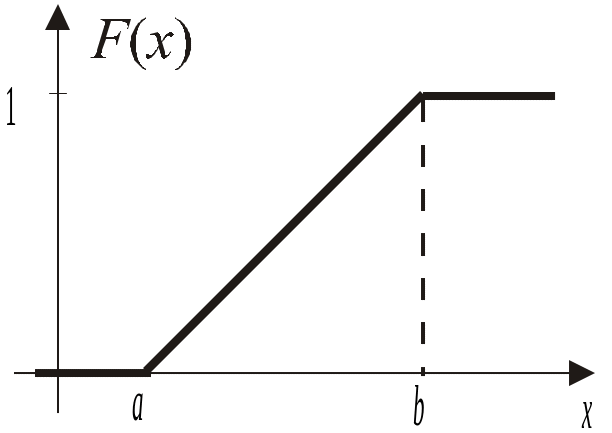
График функции F(x) представлен на рисунке 3.

Закон распределения непрерывной случайной величины можно определить заданием либо функции  (х), либо функции F(x).

Примеры абсолютно непрерывных распределений.

Равномерное непрерывное распределение было рассмотрено выше

Экспоненциальное распределение. Это распределение с плотностью ρ(х)=

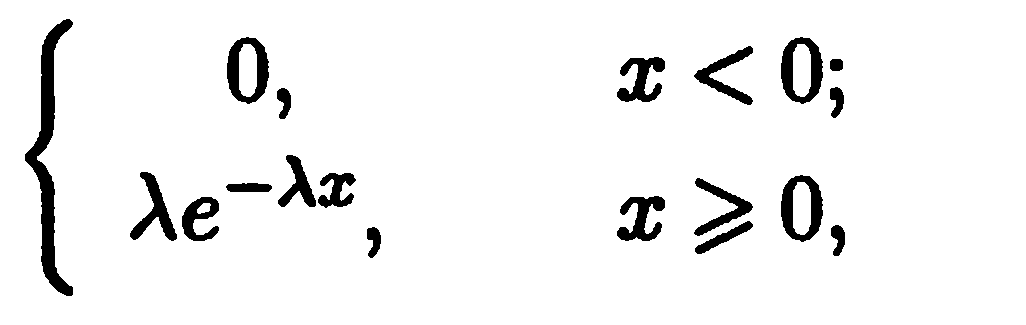, λ > 0 – параметр экспоненциального распределения, его

функция распределения имеет вид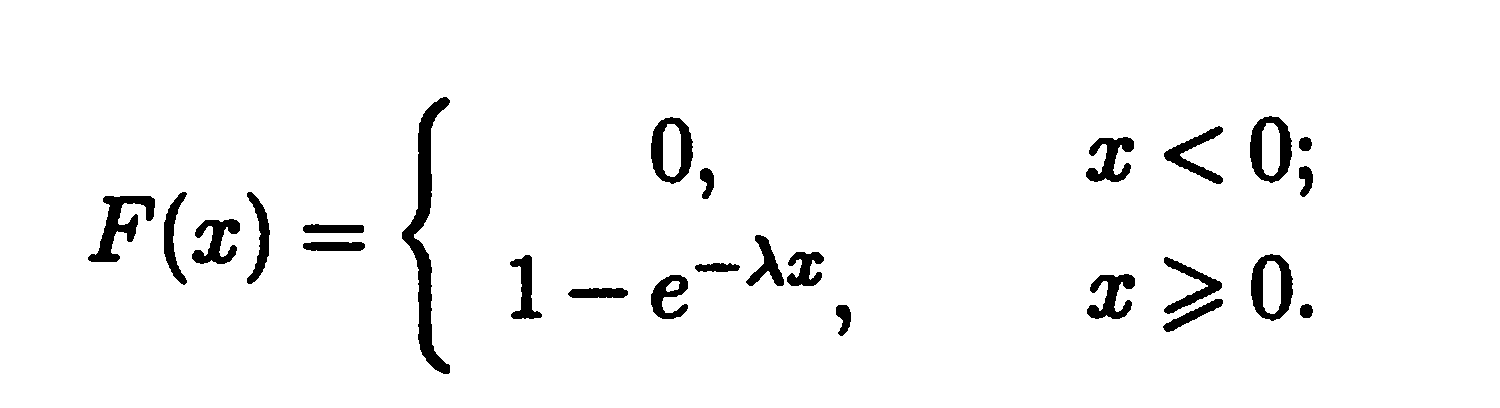

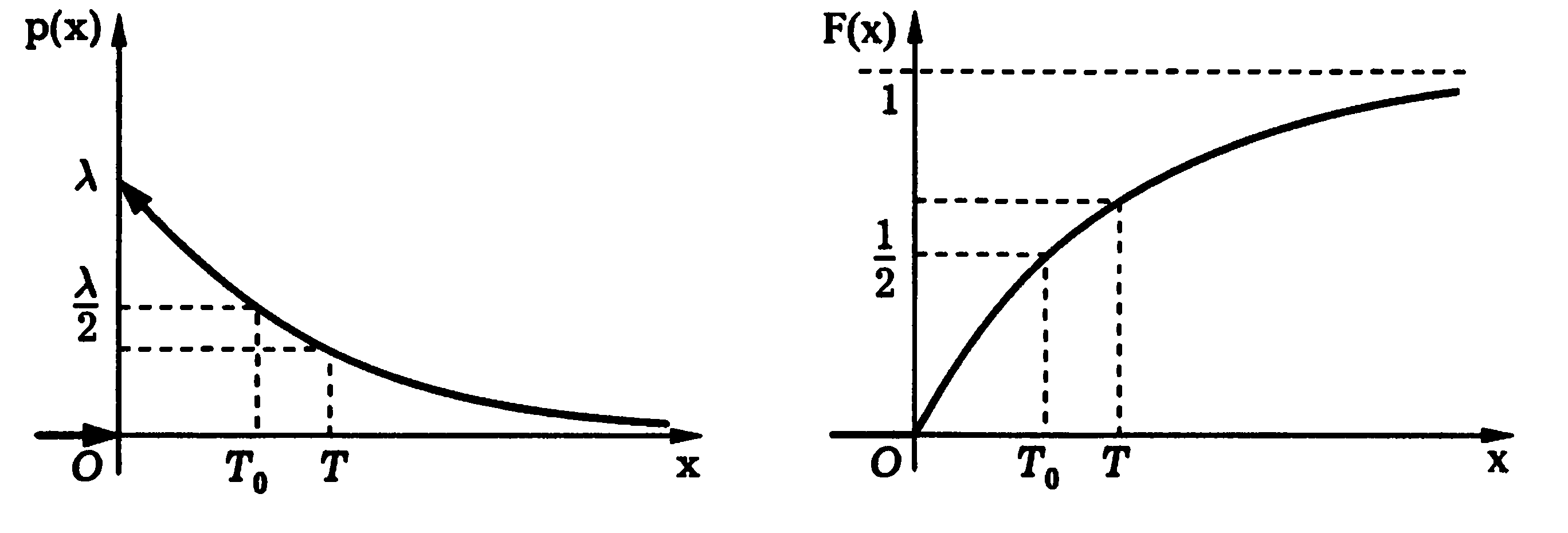
Плотность Функция распределения

Экспоненциальное распределение возникает как предельный вариант геометрического распределения. В качестве успехов и неудач рассматривается, произошло ли событие А в течение (стремящихся к нулю) промежутков времени.

Нормальное распределение.

Случайная величина имеет нормальный закон распределения c параметрами, m и σ², N (m, σ²) если ее плотность имеет вид

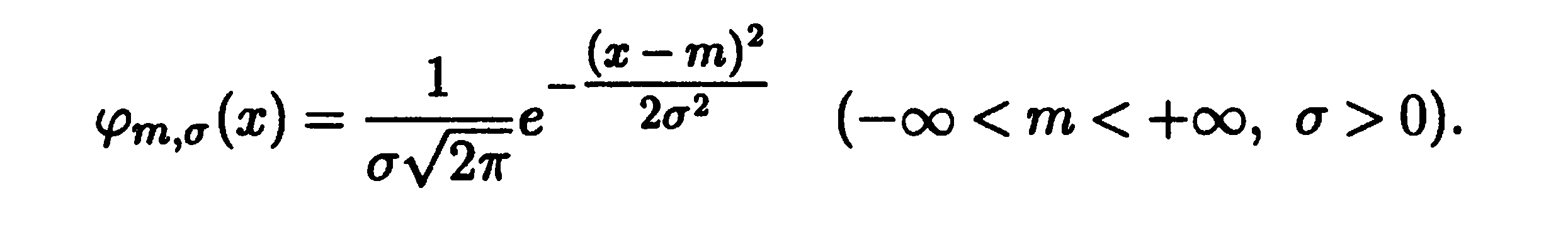
А функция распределения, соответственно,

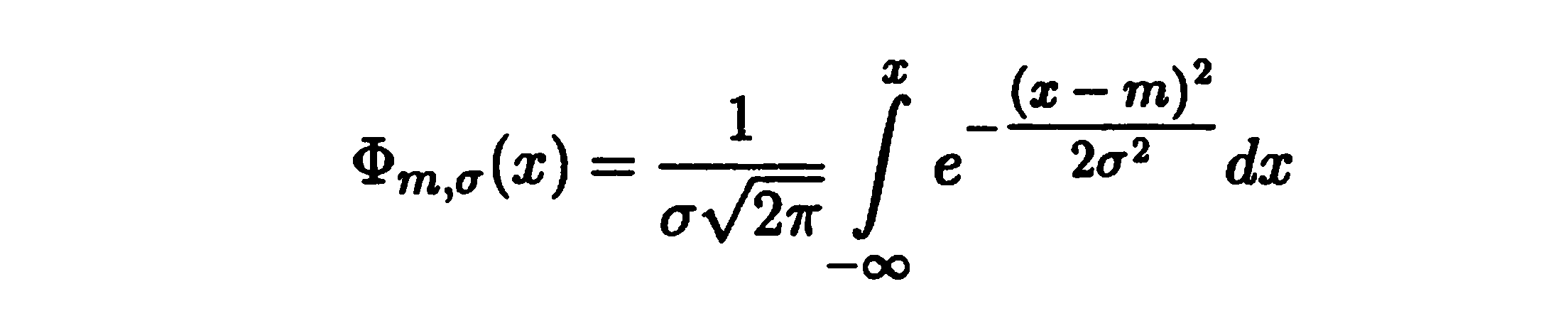
Если m=0, σ =1, распределение называется стандартным нормальным законом. Плотность в этом случае – уже известная функция Гаусса.

Поэтому в случае нормального закона плотность и функция распределения обозначаются φ и Ф, а не ρ и F.

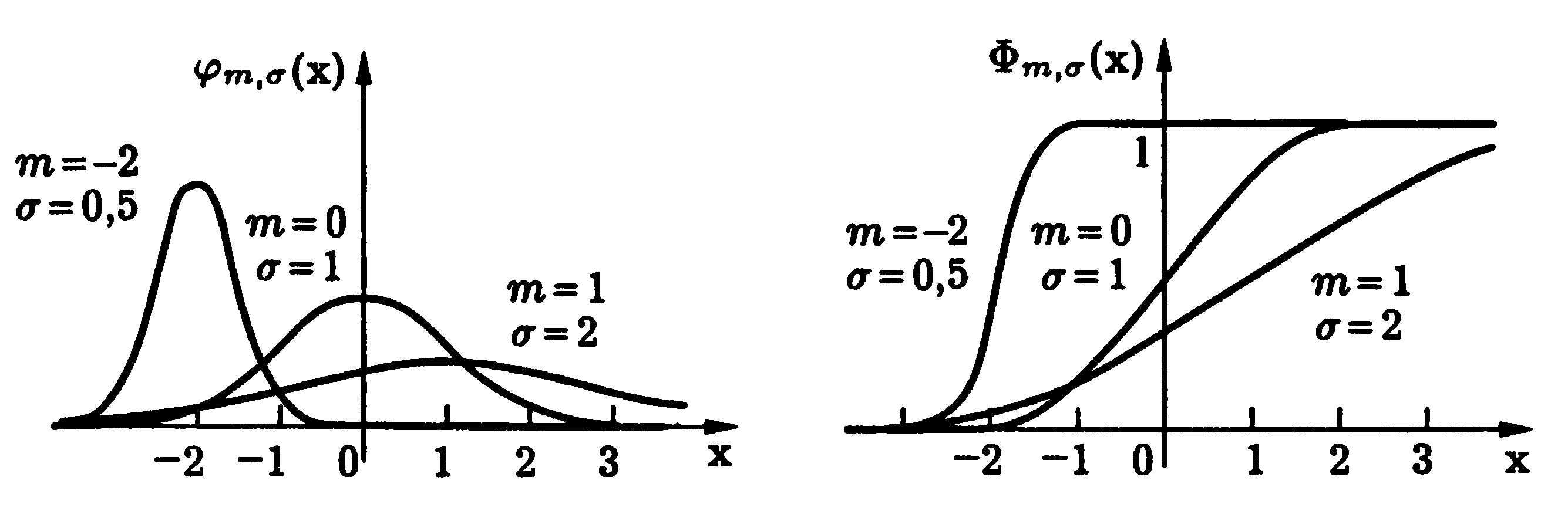
Как следует из этих рисунков, параметр m определяет положение центра симметрии плотности нормального распределения, а σ – разброс значений случайной величины относительно центра симметрии. И, соответственно,

высоту и «крутизну» пика графика плотности (чем меньше σ, тем ниже пик и медленнее стремление к нулю)

К абсолютно непрерывным распределениям относятся также крайне важные в статистической практике распределения χ² ,Стьюдента и Фишера. Но ввиду сложности формул этих распределений (они содержат гамма-функцию Эйлера), мы не будем их здесь приводить, ограничившись лишь общим описанием.

Дополнение. Распределения χ² ,Стьюдента и Фишера (по Лекциям по высшей математике А.В.Степанова)