6. Смешанное произведение векторов

Смешанным произведением трех векторов , , называется число, равное скалярному произведению вектора на вектор : . Свойства смешанного произведения

1. Смешанное произведение трех векторов равно нулю, если:

а) хотя бы один из перемножаемых векторов равен нулю;

б) два из перемножаемых векторов коллинеарны;

в) все три вектора параллельны одной и той же плоскости –компланарны.

2. Смешанное произведение не изменяется, если в нем поменять местами знаки векторного ( ) и скалярного (·) умножения, то есть

. Поэтому смешанное произведение векторов , , , записывают в виде .

3. Смешанное произведение не изменяется, если переставлять перемножаемые векторы в круговом порядке

4. При перестановке любых двух векторов смешанное произведение изменяет знак:

5. Модуль смешанного произведения трех векторов , , 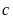равен объему параллелепипеда, построенного на этих векторах как на ребрах.

Если векторы заданы координатами

,

то их смешанное произведение найдем, вычислив определитель третьего порядка, составленный построчно из координат перемножаемых векторов

(8)

Пример 5. Показать, что векторы компланарны.

Решение. Векторы компланарны, если их смешанное произведение равно нулю. Находим

= =-49-24-6+14+9+56=-79+79=0.

Условие выполнено – векторы компланарны.

Пример 6. Найти объем треугольной пирамиды с вершинами в точках , а также высоту из вершины .

Решение.

Объем пирамиды:

.

, .

Найдем площадь основания

Высота, проведенная из вершины

.

7. Линейная зависимость векторов

Векторы называются линейно–зависимыми, если существуют такие числа , не все равные нулю, что их линейная комбинация

(9)

и линейно независимыми, если это равенство выполняется только при всех равных нулю. Если среди векторов есть нулевой вектор, то эти векторы линейно зависимы. Наличие линейной зависимости между векторами означает, что хотя бы один из них можно представить линейной комбинацией остальных.

Для того чтобы векторы были линейно независимы, необходимо и достаточно, чтобы ранг матрицы, составленной из координат этих векторов, r был равен числу векторов n. Если ранг матрицы меньше числа векторов , то векторы линейно зависимы.

Пример 7. Проверить, будут ли векторы

линейно зависимы.

Решение. Составим матрицу из координат векторов и приведем ее к ступенчатому виду

.

Ранг матрицы равен четырем и равен числу векторов, следовательно они линейно независимы.

Заметим, что два коллинеарных на плоскости, как и три компланарных вектора в трехмерном пространстве линейно зависимы.

Пример 8. Определить, при каком значении параметра векторы будут линейно зависимы.

Решение. Поскольку количество векторов равно количеству координат этих векторов, матрица из них будет квадратной, и ее ранг будет меньше числа векторов, если определитель матрицы будет равен нулю. Тогда решим уравнение

, тогда

Чтобы установить линейную зависимость между векторами, надо разложить по столбцу равный нулю определитель, составленный из координат этих векторов.

Пример 9. Установить линейную зависимость между векторами

.

Решение. Составим равный нулю определитель третьего порядка, строчками которого являются координаты данных векторов

=0

и раскроем его по элементам третьего столбца

.

Здесь подчеркнуты элементы столбца – представители соответствующих векторов, таким образом имеем линейную комбинацию , следовательно по (9) .