
- •1. Прямоугольная система координат в пространстве
- •2. Понятие вектора
- •Направляющие косинусы по (2)
- •3. Линейные операции над векторами
- •Свойства линейных операций:
- •4. Скалярное произведение векторов
- •5. Векторное произведение векторов
- •6. Смешанное произведение векторов
- •7. Линейная зависимость векторов
- •8. Базис. Размерность линейного пространства
- •9. Линейные преобразования
- •10. Собственные векторы и собственные числа линейного преобразования
3. Линейные операции над векторами
Под линейными операциями над векторами понимают операции сложения и умножение вектора на число.
Суммой
двух векторов
и
называется вектор
![]() ,
соединяющий начало вектора
с концом вектора
,
отложенного от конца вектора
,
соединяющий начало вектора
с концом вектора
,
отложенного от конца вектора
![]() .
Обозначается
.
Обозначается
![]() .
Для геометрического представления
суммы векторов используют правила
«треугольника» (рис.3) и «параллелограмма»
(
.
Для геометрического представления
суммы векторов используют правила
«треугольника» (рис.3) и «параллелограмма»
( рис.4).
рис.4).
Рис. 3.

![]()
Р
 ис.
4.
ис.
4.
Под разностью
векторов
и
понимается вектор
такой, что
![]() .
Обозначение:
.
Обозначение:
![]() .
.
Произведением
вектора
![]() на число
на число
![]() называется вектор
называется вектор
![]() ,
который имеет длину
,
который имеет длину
![]() ,направление
вектора
,
если
,направление
вектора
,
если
![]() и противоположное направление, если
и противоположное направление, если
![]() .
.
Свойства линейных операций:
 (переместительный
закон);
(переместительный
закон); (сочетательный
закон сложения);
(сочетательный
закон сложения); (сочетательный
закон умножения);
(сочетательный
закон умножения); 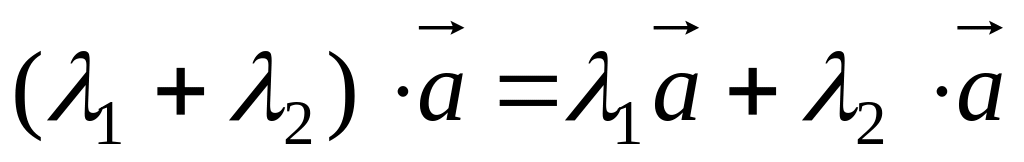 (распределительный
закон относительно сумы чисел);
(распределительный
закон относительно сумы чисел); (распределительный
закон относительно суммы векторов).
(распределительный
закон относительно суммы векторов).
4. Скалярное произведение векторов
Скалярным
произведением
векторов
и
называется число (скаляр), равное
произведению длин этих векторов на
косинус угла
![]() между ними
между ними
|
(3) |
Если хотя бы один из перемножаемых векторов нулевой, то угол неопределен и скалярное произведение по определению полагают равным нулю.
Свойства скалярного произведения:
 (переместительный
закон)
(переместительный
закон)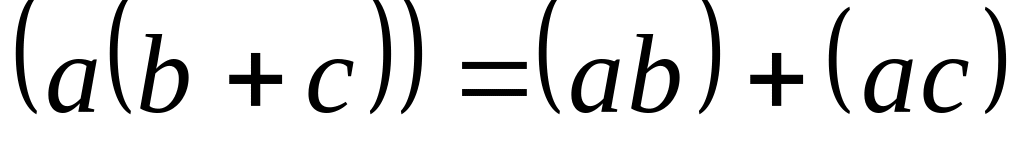 (распределительный
закон)
(распределительный
закон) (сочетательный
закон по отношению к скалярному
множителю)
(сочетательный
закон по отношению к скалярному
множителю) - скалярный
квадрат вектора, неотрицательное число,
равное квадрату длины вектора.
- скалярный
квадрат вектора, неотрицательное число,
равное квадрату длины вектора. ,
если
=0,
либо
=0,
либо
перпендикулярен
.
,
если
=0,
либо
=0,
либо
перпендикулярен
.
Если векторы заданы
координатами
![]() , то
скалярное произведение равно сумме
парных произведений одноименных
координат, то есть его удобно находить
по формуле
, то
скалярное произведение равно сумме
парных произведений одноименных
координат, то есть его удобно находить
по формуле
|
(4) |
Косинус угла между векторами
|
(5) |
Пример 2. Найти
скалярное произведение векторов:
![]() и
и
![]() и угол между ними.
и угол между ними.
Решение. Скалярное произведение находим по формуле (4):
=![]() -
-![]() +
+![]() =6-20+14=0,
значит, вектора перпендикулярны.
=6-20+14=0,
значит, вектора перпендикулярны.
Пример 3. Найти
скалярное произведение векторов
![]() ,
если
,
если
![]() .
.
Решение:
![]() .
.
5. Векторное произведение векторов
Векторным
произведением
вектора
на вектор
называется третий вектор
![]() ,
определяемый следующим образом (рис.
5):
,
определяемый следующим образом (рис.
5):

![]()
![]()



φ

![]()
Рис. 5.
1) модуль вектора равен произведению длин перемножаемых векторов на синус угла между ними
|
(6) |
2) вектор
![]() перпендикулярен перемножаемым векторам
и
;
перпендикулярен перемножаемым векторам
и
;
3) векторы , , после приведения к общему началу ориентированы по отношению друг к другу соответственно как орты i, j, k (в правой системе координат образуют так называемую правую тройку векторов).
Модуль векторного произведения равен площади параллелограмма, построенного на векторах и как на сторонах.
Свойства векторного произведения:
 то есть векторное
произведение не обладает переместительным
свойством;
то есть векторное
произведение не обладает переместительным
свойством; (сочетательный
закон по отношению к скалярному
множителю);
(сочетательный
закон по отношению к скалярному
множителю); (распределительный
закон);
(распределительный
закон); ,
если
= 0,
либо
= 0, либо
вектора коллинеарны
||
.
,
если
= 0,
либо
= 0, либо
вектора коллинеарны
||
.
Векторные
произведения координатных ортов
![]()
![]()
![]() ;
;
![]() .
.
Если векторы заданы
координатами
,
то их векторное
произведение есть вектор, координаты
которого получим, раскрыв по первой
строке определитель третьего порядка,
в первой строке которого орты
![]() ,
во второй и третьей – координаты
перемножаемых векторов
,
во второй и третьей – координаты
перемножаемых векторов
|
(7) |
Пример 4. Вычислить
площадь параллелограмма, построенного
на векторах
![]() .
.
Решение. Найдем векторное произведение (7)
 .
.
Площадь параллелограмма равна модулю векторного произведения
S=![]() =
=![]() =49
(кв. ед).
=49
(кв. ед).

