
- •Глава I Классическое и квантовое описание оптического поля
- •§ 1. Коментарии к постулатам квантовой механики и квантовой оптики
- •§ 2. Классический гармонический осциллятор
- •§3. Квантовый гармонический осциллятор в стационарном состоянии
- •§ 4. Квантовый гармонический осциллятор в когерентном состоянии
- •5. Квантование электромагнитного поля в вакууме
- •§ 6. Уравнения максвелла для поля в среде
- •§ 7. Когерентность и монохроматичность электромагнитного поля
- •Глава II Распространение электромагнитной волны в нелинейной среде
- •§ 8. Общие представления о нелинейном отклике среды
- •§ 9. Нелинейная геометрическая оптика
- •§ 10. Нелинейное параболическое уравнение
- •§ 11. Устойчивость плоской волны в нелинейной среде
- •§ 12. Солитоны
- •§ 13. Самофокусировка и самоканализация
- •Глава III Нелинейные восприимчивости
- •§14. Нелинейная связь между поляризацией и электрическим полем
- •§15. Классификация нелинейно-оптических эффектов
- •§16. Модель ангармонического осциллятора
- •§17. Общая теория нелинейных восприимчивостей для произвольной квантовомеханической системы
- •Глава IV
- •§18. Генерация оптических гармоник
- •§19. Пространственный синхронизм
- •§20. Резонансная генерация третьей гармоники
- •§21. Методы создания фазового согласования
- •22. Параметрические взаимодействия
- •§23. Вынужденное рассеяние мандельштама-бриллюэна (врмб)
- •4.Правило нахождения Гамильтониана
- •5.Постулат тождественности
§ 6. Уравнения максвелла для поля в среде
В классической физике электромагнитное поле описывается уравнениями Максвелла. Они определяют величину электрического и магнитного полей в пространстве и времени по заданному распределению зарядов и токов. Если среда достаточно плотная, так что среднее расстояние между частицами среды весьма мало по сравнению с характерными длинами волн, то в уравнениях Максвелла можно
перейти от микроскопических величин, определяемых в данной точке пространства, к средним значениям вблизи этих точек. Причем усреднение проводится по объемам, размеры которых заведомо превосходят межатомные, но значительно меньше длины волны. Такая процедура справедлива для оптического диапазона в конденсированных средах – жидкостях, твердых телах и плотных газах, но становится неверной в далеком ультрафиолетовом и рентгеновском диапазонах.
Уравнения Максвелла для усредненных сред имеют вид (5.2), в эти уравнения необходимо ввести дополнительное слагаемое с током
![]() (6.1)
(6.1)
![]() (6.2)
(6.2)
причем
каждая из макроскопических величин
![]() ,
,
![]() и
и
![]() является средней по малым объемам
соответствующих микроскопических
величин. К уже написанным уравнениям
обычно добавляют два других:
является средней по малым объемам
соответствующих микроскопических
величин. К уже написанным уравнениям
обычно добавляют два других:
![]() ,
,
![]() ,
(6.3)
,
(6.3)
которые
являются следствием предыдущих, в чем
можно убедиться, если учесть, что
![]()
![]() и
уравнение непрерывности для плотности
тока и зарядов
и
уравнение непрерывности для плотности
тока и зарядов
![]() .
(6.4)
.
(6.4)
Иногда на практике более удобной оказывается иная форма записи уравнений Максвелла. Введем вектор электрической индукции:
![]() .
(6.5)
.
(6.5)
Если
подействовать оператором
![]() на левую и правую стороны уравнения
(6.2) и после этого подставить в него
уравнение (6.1), то с учетом последнего
выражения (6.5) получим уравнение
на левую и правую стороны уравнения
(6.2) и после этого подставить в него
уравнение (6.1), то с учетом последнего
выражения (6.5) получим уравнение
![]() ,
(6.6)
,
(6.6)
которым будем широко пользоваться в последующих главах.
Средняя плотность тока создается в среде внешними полями или проходящими через среду внешними зарядами, и вид тока определяется конкретным состоянием вещества. При прохождении электромагнитных волн через среду наведенный ток представляет собой сложную функцию электрического и магнитного полей, а также его производных по координатам и времени.
Для таких сред, как классическая плазма, электроны в металле, носители тока в полупроводниках, ток определяется посредственным движением зарядов под действием лоренцовой силы, при этом только необходимо правильно учитывать кинематику движения электронов в твердых телах (закон дисперсии). Вычисление тока в этом случае предполагает решение соответствующего кинетического уравнения.
Для
диэлектриков и полупроводников без
носителей тока представлять ток удобно
в виде ряда по мультипольным моментам.
Так как область движения локализованных
электронов ограничена атомными
расстояниями, то в оптическом диапазоне
выражению тока через мультипольные
моменты эквивалентно разложению в ряд
по малому параметру
![]() .
.
Разложение тока по мультипольным моментам произведем следующим образом: запишем микроскопическую плотность тока
![]() ,
(6.7)
,
(6.7)
где суммирование проводится по всем заряженным частицам среды. Очевидно, что возникает цепочка тождеств:
![]() ,
(6.8)
,
(6.8)
где
![]() .
Далее, последнее слагаемое преобразуем,
используя равенства
.
Далее, последнее слагаемое преобразуем,
используя равенства
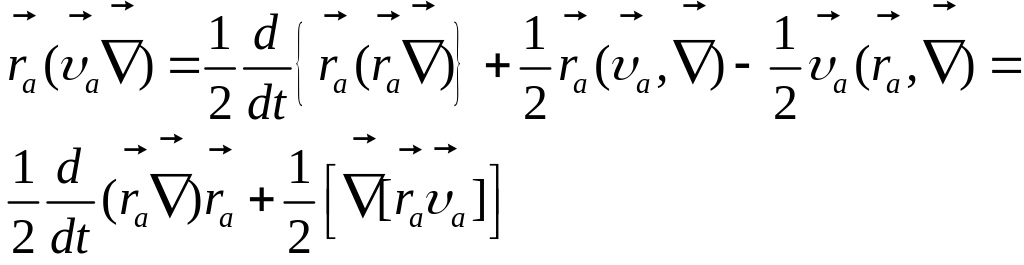 (6.9)
(6.9)
С учетом (6.8) и (6.9) выражение для тока запишем так:
![]() .
(6.10)
.
(6.10)
первый член в выражении (6.10) содержит плотность дипольного момента
![]() ,
(6.11)
,
(6.11)
второй член – плотность магнитодипольного момента среды
![]() ,
(6.12)
,
(6.12)
третий – плотность квадрупольного момента
![]() .
(6.13)
.
(6.13)
Дипольный
момент пропорционален первой степени
![]() ,
магнито-дипольный и квадрупольный
содержат квадратичные комбинации типа
,
магнито-дипольный и квадрупольный
содержат квадратичные комбинации типа
![]() и
и
![]() ,
последующие мультипольные моменты
будут содержать более высокие степени
для координат и скорости частиц.
,
последующие мультипольные моменты
будут содержать более высокие степени
для координат и скорости частиц.
Четвертый член
![]() .
(6.14)
.
(6.14)
Выделение последующих мультипольных моментов производится по аналогии с вышеизложенной процедурой.
Произведем
усреднение по малым объемам
![]() вблизи точки
вблизи точки
![]() ,
то есть перейдем от рассмотрения
микроскопического тока к макроскопическому:
,
то есть перейдем от рассмотрения
микроскопического тока к макроскопическому:
![]() .
(6.15)
.
(6.15)
Для первых трех моментов получим
![]() ;
;
![]() ;
;
![]() .
(6.16)
.
(6.16)
Эти макроскопические величины являются функциями координаты . Суммирование здесь проводится по числу частиц, содержащихся в единице объема. Выражение для макроскопического тока совпадает с (6.10).
Относительно полученных усреднений моментов (6.11) – (6.13) необходимо сделать важное замечание: эти моменты определены неоднозначно и зависят от выбора определенной системы координат. Только при специальных условиях эти выражения определяют моменты однозначно. Действительно, пусть моменты определены в двух системах отсчета, радиусы-векторы в которых связаны между собой через некоторый постоянный вектор
![]() .
(6.17)
.
(6.17)
Для дипольных моментов связь будет выражена таким образом:
![]() .
(6.18)
.
(6.18)
Следовательно,
дипольный момент определен однозначно
лишь в том случае, когда заряд единичного
объема среды равен нулю:
![]() .
Для магнитодипольных моментов связь
имеет вид
.
Для магнитодипольных моментов связь
имеет вид
![]() ,
(6.19)
,
(6.19)
откуда
следует, что однозначное определение
магнитного момента соответствует
условию:
![]() ,
то есть в том случае, когда вклад в
усредненный ток от первого члена
выражения (6.10) равен нулю. Наконец, связь
квадрупольных моментов описывается
формулой
,
то есть в том случае, когда вклад в
усредненный ток от первого члена
выражения (6.10) равен нулю. Наконец, связь
квадрупольных моментов описывается
формулой
![]() ,
(6.20)
,
(6.20)
Из
которой легко заключить, что для
однозначного определения квадрупольного
момента необходимы условия:
![]() и
.
В этом случае более удобно определить
квадрупольный момент как
и
.
В этом случае более удобно определить
квадрупольный момент как
![]() .
(6.21)
.
(6.21)
Последнее
слагаемое дает нулевой вклад в ток
(6.10), но поскольку сумма диагональных
элементов тензора
![]() ,
то независимыми являются лишь два (из
трех) главных значения.
,
то независимыми являются лишь два (из
трех) главных значения.
В
случае, когда движение валентных
электронов ограничено атомными
расстояниями и оптическими частотами,
выражение для тока (6.10) есть разложение
по малому параметру
.
Действительно, полагая
![]() ;
;
![]() в (5.10), находим:
в (5.10), находим:
![]() ;
;
![]() ;
;
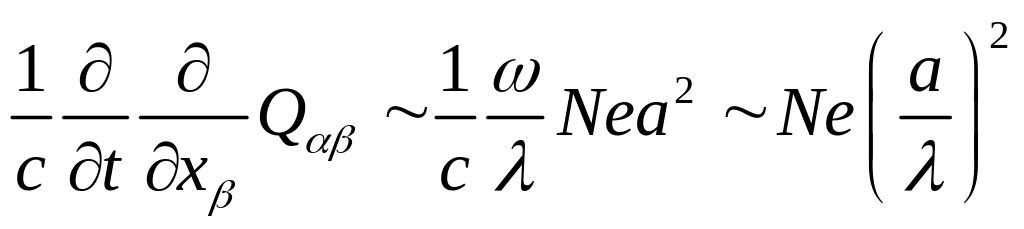 ,
,
где
![]() - плотность молекул конденсированного
вещества.
- плотность молекул конденсированного
вещества.
Далее, умножая скалярно уравнение Максвелла (6.1) на величину электрического поля , а уравнение (6.2) – на и вычитая из первого второе, получим после векторных преобразований уравнение сохранения энергии
![]() .
(6.22)
.
(6.22)
Для
вакуума, где ток равен нулю (![]() ),
последнее можно записать в виде уравнения
непрерывности:
),
последнее можно записать в виде уравнения
непрерывности:
![]() ,
(6.23)
,
(6.23)
где поток энергии электромагнитного поля
![]() ,
(6.24)
,
(6.24)
а плотность энергии
![]() (6.25)
(6.25)
Последний член в (6.22) описывает взаимодействие поля с веществом. Подчеркнем, что этот член не только показывает влияние вещества на плотность энергии в единице объема, но также приводит к изменению потока энергии. Действительно, подставим выражение для тока (6.10) в (6.22) и после простых преобразований получим уравнение типа (6.23), где поток и плотность энергии определяются формулами
![]()
![]() ,
,
где
![]() ;
;
![]() .
.
Таким образом, вектор Умова-Пойнтинга включает в себя магнитодипольные и квадрупольные эффекты, а плотность энергии содержит изменение энергии электромагнитного поля (6.25), а также включает работу, производимую электромагнитным полем над веществом.
