
- •Глава I Классическое и квантовое описание оптического поля
- •§ 1. Коментарии к постулатам квантовой механики и квантовой оптики
- •§ 2. Классический гармонический осциллятор
- •§3. Квантовый гармонический осциллятор в стационарном состоянии
- •§ 4. Квантовый гармонический осциллятор в когерентном состоянии
- •5. Квантование электромагнитного поля в вакууме
- •§ 6. Уравнения максвелла для поля в среде
- •§ 7. Когерентность и монохроматичность электромагнитного поля
- •Глава II Распространение электромагнитной волны в нелинейной среде
- •§ 8. Общие представления о нелинейном отклике среды
- •§ 9. Нелинейная геометрическая оптика
- •§ 10. Нелинейное параболическое уравнение
- •§ 11. Устойчивость плоской волны в нелинейной среде
- •§ 12. Солитоны
- •§ 13. Самофокусировка и самоканализация
- •Глава III Нелинейные восприимчивости
- •§14. Нелинейная связь между поляризацией и электрическим полем
- •§15. Классификация нелинейно-оптических эффектов
- •§16. Модель ангармонического осциллятора
- •§17. Общая теория нелинейных восприимчивостей для произвольной квантовомеханической системы
- •Глава IV
- •§18. Генерация оптических гармоник
- •§19. Пространственный синхронизм
- •§20. Резонансная генерация третьей гармоники
- •§21. Методы создания фазового согласования
- •22. Параметрические взаимодействия
- •§23. Вынужденное рассеяние мандельштама-бриллюэна (врмб)
- •4.Правило нахождения Гамильтониана
- •5.Постулат тождественности
5. Квантование электромагнитного поля в вакууме
Рассмотрим классическое описание электромагнитного поля в вакууме. Пусть поле заключено в некоторую полость объемом V c идеально отражающей металлической поверхностью S, т.е. в некоторый резонатор. В этой модели на поверхности S будет выполняться условие
![]() (5.1)
(5.1)
где
![]() - нормаль к внутренней стороне поверхности.
Условие (5.1) означает, что тангенциальная
составляющая напряженности электрического
поля в точках поверхности равна нулю.
Электромагнитное, в том числе и оптическое,
поле в вакууме описывается уравнениями
Максвелла
вида:
- нормаль к внутренней стороне поверхности.
Условие (5.1) означает, что тангенциальная
составляющая напряженности электрического
поля в точках поверхности равна нулю.
Электромагнитное, в том числе и оптическое,
поле в вакууме описывается уравнениями
Максвелла
вида:
![]()
(5.2)
![]()
которые
путем повторного применения операции
![]() легко
преобразуются в уравнения для каждого
поля - электрического
легко
преобразуются в уравнения для каждого
поля - электрического
![]() и магнитного
и магнитного
![]() -
в отдельности
-
в отдельности
![]()
(5.3)
![]()
Ищем решения последних уравнений методом разделения переменных, полагая, что
![]() (5.4)
(5.4)
где знак минус выбран для удобства в дальнейшем (см. ниже). Подставляя (5.4) в первое уравнение системы (5.3), получим
![]()
(5.5)
![]()
где
![]() .
Величина
.
Величина
![]() ;
в противном случае появляются нефизические
решения, нарастающие со временем. Для
магнитного поля используем аналогичную
процедуру: ищем решение в виде произведения
функций с разделяющимися переменными,
т.е.
;
в противном случае появляются нефизические
решения, нарастающие со временем. Для
магнитного поля используем аналогичную
процедуру: ищем решение в виде произведения
функций с разделяющимися переменными,
т.е.
![]() (5.6)
(5.6)
где
выбор множителя в виде![]() станет ясным из последующего изложения
( см. (5.13)). Подставляя (5.6) во второе
уравнение системы (5.3), получим, что
уравнения для нахождения
станет ясным из последующего изложения
( см. (5.13)). Подставляя (5.6) во второе
уравнение системы (5.3), получим, что
уравнения для нахождения
![]() и
и
![]() имеют вид, в точности совпадающий с
(5.5), именно:
имеют вид, в точности совпадающий с
(5.5), именно:
![]()
(5.7)
![]()
Если подставить (5.4) и (5.6) в исходные уравнения (5.2), то для функций от пространственных переменных получим уравнения
![]()
(5.8)
![]()
а для функций от времени
![]()
(5.9)
![]()
где
точка сверху означает дифференцирование
по времени. Уравнения (5.9) совпадают с
уравнениями Гамильтона для классического
гармонического осциллятора (2.5). Второе
уравнение для
![]() в (5.5) и аналогичное для
в (5.7) совпадают с классическими уравнениями
(2.7). Далее следует отметить, что из
первого уравнения (5.5) с учетом граничного
условия (5.1) легко получить свойство
ортогональности для функций
в (5.5) и аналогичное для
в (5.7) совпадают с классическими уравнениями
(2.7). Далее следует отметить, что из
первого уравнения (5.5) с учетом граничного
условия (5.1) легко получить свойство
ортогональности для функций
![]() ,
которое запишем в виде
,
которое запишем в виде
![]() (5.10)
(5.10)
Здесь
под знаком интеграла стоит скалярное
произведение векторов
,
которые таким образом выбираются
нормированными на единицу. Аналогичное
условие нормировки справедливо для
![]() .
.
Любое
произвольное электромагнитное ( в том
числе и оптическое ) поле в резонаторе
можно представить в виде разложения по
полной ортонормированной системе
функций типа (5.4) и (5.6). Обычно граничные
условия типа (5.1) или периодического
типа ( см. далее ) выделяют некоторый
набор дискретных значений волновых
чисел![]() .
При определенном
в резонаторе существует вполне
определенная конфигурация электромагнитного
поля, осциллирующая на определенной
частоте
.
При определенном
в резонаторе существует вполне
определенная конфигурация электромагнитного
поля, осциллирующая на определенной
частоте
![]() .
Это конкретное состояние электромагнитного
поля в резонаторе называется модой
поля. Таким образом, произвольное
электромагнитное поле в резонаторе
представляется в виде суммы по модам
поля, а именно:
.
Это конкретное состояние электромагнитного
поля в резонаторе называется модой
поля. Таким образом, произвольное
электромагнитное поле в резонаторе
представляется в виде суммы по модам
поля, а именно:
![]()
(5.11)
![]()
Множитель
![]() выбран из соображений, которые станут
ясны из дальнейшего рассмотрения. Полная
энергия поля в резонаторе
выбран из соображений, которые станут
ясны из дальнейшего рассмотрения. Полная
энергия поля в резонаторе
![]() (5.12)
(5.12)
которая для полей (5.11) с учетом условия ортонормированности (5.10) принимает окончательный вид
![]() (5.13)
(5.13)
что представляет собой сумму гамильтоновых функций гармонических осцилляторов типа (1.4). Произведенный выше выбор коэффициентов в (5.6) и в (5.11) обеспечивает получение (5.13).
Из вида (5.13) следует, что в классической физике электромагнитное поле в замкнутом пространстве можно рассматривать как дискретный ансамбль независимых гармонических осцилляторов.
Квантование
электромагнитного поля в этом случае
сводится к квантованию гармонических
осцилляторов: в квантовой теории вместо
классических динамических переменных
и
вводятся линейные эрмитовые операторы
![]()
и
![]() , которые удовлетворяют известному
коммутационному соотношению
, которые удовлетворяют известному
коммутационному соотношению
![]() (5.14)
(5.14)
Аналогично тому, как это рассматривалось в предыдущих параграфах этой главы ( см. § 1.3 и § 1.4 ), вместо операторов координаты и импульса удобно ввести операторы рождения и уничтожения фотона -ой моды в соответствии с (3.20) формулами вида:
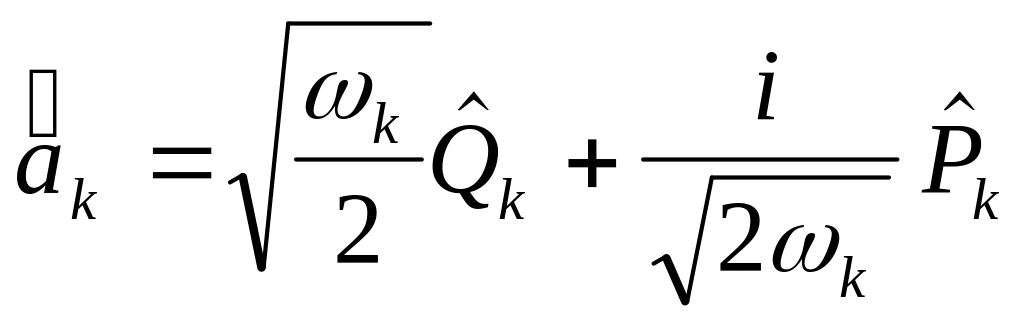
(5.15)
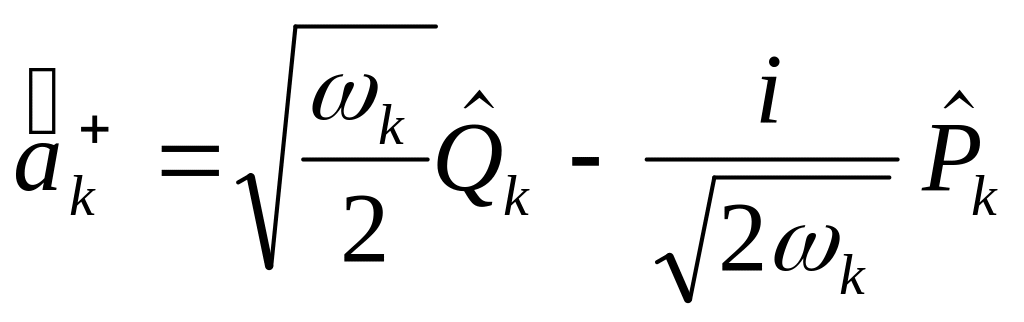
Гамильтониан
электромагнитного поля в операторах
![]() и
и
![]() , соответствующий функции Гамильтона
(5.13) принимает вид суммы гамильтонианов
одномерных гармонических осцилляторов
(3.24), а именно
, соответствующий функции Гамильтона
(5.13) принимает вид суммы гамильтонианов
одномерных гармонических осцилляторов
(3.24), а именно
![]() (5.16)
(5.16)
где суммирование осуществляется по всем модам, или, иными словами, по всем фотонам. Дело в том, что при квантовании электромагнитного поля вместо оператора чисел заполнения вида (3.30), который характеризует номер энергетического уровня одномерного осциллятора, появляется оператор вида:
![]() (5.17)
(5.17)
который называют оператором числа фотонов -ой моды, или просто оператором числа частиц, подразумевая под ними кванты электромагнитного поля - фотоны. Очевидно, что оператор полного числа частиц определяется суммой
![]() (5.18)
(5.18)
где
суммирование происходит по всем модам,
т.е. по набору дискретных чисел
.
В общем случае, как это будет видно из
дальнейшего, каждое
состоит из волнового вектора фотона
![]() и одного из двух значений поляризации
фотона
и одного из двух значений поляризации
фотона
![]() .
При непрерывных величинах компонент
волнового вектора вместо суммирования
в предыдущих и в последующих выражениях
необходимо производить интегрирование,
т.е. произвести замену
.
При непрерывных величинах компонент
волнового вектора вместо суммирования
в предыдущих и в последующих выражениях
необходимо производить интегрирование,
т.е. произвести замену
![]() (5.19)
(5.19)
Операторы
напряженностей электрического и
магнитного полей
![]() и
и
![]() определяются выражениями (5.11), в которых
динамические переменные
определяются выражениями (5.11), в которых
динамические переменные
![]() и
и
![]() заменяются на эрмитовые операторы
и
.
Выражая
и
через
и
из соотношений (5.15) и подставляя в (5.11)
получаем операторы для каждой j-ой
проекции полей в следующей форме:
заменяются на эрмитовые операторы
и
.
Выражая
и
через
и
из соотношений (5.15) и подставляя в (5.11)
получаем операторы для каждой j-ой
проекции полей в следующей форме:
![]()
(5.20)
![]()
где операторы рождения и уничтожения фотонов различных мод и проекций подчиняются коммутационному соотношению
![]() (5.21)
(5.21)
которое является естественным обобщением соотношения (3.23).
Значение дискретных частот зависит от размеров полости и формы ограничивающей её поверхности конкретного резонатора. С увеличением объема резонатора интервалы значений между ближайшими частотами уменьшаются. Если интересоваться не значениями частот , а плотностью частот в некотором интервале, то для объемов, значительно превосходящих по своим линейным размерам характерные длины оптических волн, плотность частот не будет зависеть от формы поверхности резонатора.
Проведенный
выше анализ относился, по существу, к
случаю стоячих волн, так как мы имели
дело с ограниченным объемом полости
резонатора и молчаливо предполагали
внутренний объем однородным, односвязанным,
т.е. не содержащим включений, делающих
его похожим на торообразные, кольцевые
формы. В последнем случае возникнут
моды бегущих волн. Кроме этого, при
рассмотрении оптических полей в
неограниченном пространстве более
естественно и правильно представлять
оптические поля в виде разложений по
бегущим волнам ( т.е. интегралом Фурье).
В этом случае принято поступать следующим
образом. Мысленно выделяют в неограниченном
пространстве конечный объем в виде
куба, ребро которого длины
![]() много больше характерной длины волны
оптического поля
много больше характерной длины волны
оптического поля
![]() .
Затем в качестве граничных условий
берут условие периодичности поля на
противоположных гранях куба, например
.
Затем в качестве граничных условий
берут условие периодичности поля на
противоположных гранях куба, например
![]() .
Этот прием позволяет получить дискретный
ряд значений компонент волновых векторов
бегущих волн. В конечных результатах
необходимо длину ребра куба устремить
в бесконечность (
.
Этот прием позволяет получить дискретный
ряд значений компонент волновых векторов
бегущих волн. В конечных результатах
необходимо длину ребра куба устремить
в бесконечность (![]() ).
).
При таком подходе решение волновых уравнений (5.3) нужно искать не в виде стоячих волн (5.4), а в виде плоской монохроматической бегущей волны
![]() (5.22)
(5.22)
где
![]() означает "комплексно-сопряженное",
а
означает "комплексно-сопряженное",
а
![]() и
и
![]() есть обозначение положительно- частотного
и отрицательно-частотного слагаемого
амплитуды поля. Эти слагаемые комплексно
сопряжены друг с другом, т.е.
есть обозначение положительно- частотного
и отрицательно-частотного слагаемого
амплитуды поля. Эти слагаемые комплексно
сопряжены друг с другом, т.е.
![]() .
Из периодических граничных условий
следует , что допустимые значения
компонент волнового вектора
.
Из периодических граничных условий
следует , что допустимые значения
компонент волнового вектора
![]() равны
равны
![]()
![]()
![]() (5.23)
(5.23)
где
![]() - целые числа.
- целые числа.
Операторы электромагнитного поля, выраженные через моды плоских бегущих волн, примут следующий вид (сравни с (5.20)):
![]() (5.24)
(5.24)
![]() (5.25)
(5.25)
Здесь
последнее выражение (5.25) записано в
гауссовой системе единиц (esu),
а
![]() есть вектор поляризации фотона. Для
поперечных волн он перпендикулярен
волновому вектору
.
Система функций (5.25) ортогональная.
Удобство выбора нормировочного множителя
перед
есть вектор поляризации фотона. Для
поперечных волн он перпендикулярен
волновому вектору
.
Система функций (5.25) ортогональная.
Удобство выбора нормировочного множителя
перед
![]() в том виде, как это сделано в (5.25) станет
ясно из дальнейшего изложения (см. (5.32)
и (5.33)). Оператор
в том виде, как это сделано в (5.25) станет
ясно из дальнейшего изложения (см. (5.32)
и (5.33)). Оператор
![]() в (5.24) описывает ту часть оптического
поля, которая содержит положительные
частоты. Второе слагаемое
в (5.24) описывает ту часть оптического
поля, которая содержит положительные
частоты. Второе слагаемое
![]() в
(5.24) содержит отрицательные частоты.
Это полностью соответствует классическому
описанию, когда реальное оптическое
поле представляют в виде двух
комплексно-сопряженных слагаемых, как
это видно из формулы для плоской
монохроматической волны (5.22). Операторы
и
представляют комплексные ( а не реальные
) поля. Тем не менее они гораздо более
удобны при изучении квантовой оптики.
Эти операторы являются эрмитовосопряженными
друг относительно друга. Из определений,
даваемых формулой (5.24), видно, что оператор
описывает уничтожение (поглощение)
фотона, а оператор
- его рождение (испускание).
в
(5.24) содержит отрицательные частоты.
Это полностью соответствует классическому
описанию, когда реальное оптическое
поле представляют в виде двух
комплексно-сопряженных слагаемых, как
это видно из формулы для плоской
монохроматической волны (5.22). Операторы
и
представляют комплексные ( а не реальные
) поля. Тем не менее они гораздо более
удобны при изучении квантовой оптики.
Эти операторы являются эрмитовосопряженными
друг относительно друга. Из определений,
даваемых формулой (5.24), видно, что оператор
описывает уничтожение (поглощение)
фотона, а оператор
- его рождение (испускание).
В ряде случаев в дальнейшем целесообразно представлять оптическое поле с помощью векторного потенциала. Например, в следующем виде:
![]() ,
,
![]() (5.26)
(5.26)
Для оператора векторного потенциала при рассматриваемом способе разложения справедлива формула
![]() (5.27)
(5.27)
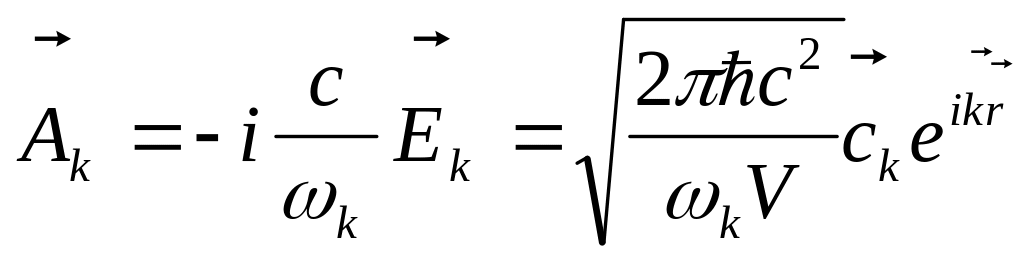 (5.28)
(5.28)
(последнее выражение записано в гауссовой системе единиц).
Из (5.26) (5.27) и (5.28)для магнитного поля получаем
![]() ,
,
![]() (5.29)
(5.29)
Матричные
элементы операторов
и
даются выражениями (3.28), где
![]() заменяется на
заменяется на
![]() .
.
Итак, все полученные в предыдущем параграфе выводы легко обобщаются на электромагнитное поле как на ансамбль осцилляторов. В частности, в соответствии с определением (4.1) когерентное состояние оптического поля есть состояние, которое является собственной функцией ( вектором) оператора :
![]() (5.30)
(5.30)
где
![]() (5.31)
(5.31)
![]() (5.32)
(5.32)
Из
ранее полученных выражений (2.14) и (4.23)
для
![]() легко получаем, что
легко получаем, что
![]() (5.33)
(5.33)
и все результаты из § 1.4 целиком и полностью применимы к одной моде оптического поля.
Для
больших чисел фотонов в одной моде (![]() )
собственное значение
)
собственное значение
![]() совпадает с классическим определением
положительно-частотной амплитуды
оптического поля. В этом предельном
случае для каждой моды соотношение
неопредленности для числа фотонов и
фазы имеет минимально возможное значение,
а именно из (4.46) имеем
совпадает с классическим определением
положительно-частотной амплитуды
оптического поля. В этом предельном
случае для каждой моды соотношение
неопредленности для числа фотонов и
фазы имеет минимально возможное значение,
а именно из (4.46) имеем
![]() (5.34)
(5.34)
Из
(4.24) видно, что в рассматриваемом
случае![]() <<
<<![]() ,
и, следовательно, с учетом этого из
(5.34) получим:
,
и, следовательно, с учетом этого из
(5.34) получим:
![]() .
Таким образом, в классическом пределе
значению фазы и амплитуды оптического
поля соответствуют достаточно определенные
величины: точность их определения тем
выше, чем больше число фотонов в каждой
моде.
.
Таким образом, в классическом пределе
значению фазы и амплитуды оптического
поля соответствуют достаточно определенные
величины: точность их определения тем
выше, чем больше число фотонов в каждой
моде.
