Тема 5. Смешанные стратегии

Среди антагонистических игр, моделирующих практические конфликты, существенную долю составляют игры без седловых точек, т.е. игры, в которых нижняя цена игры строго меньше верхней цены : . Если такая игра состоит из единственной "партии", т.е. каждый из игроков А и В делает только один ход, предполагая, что его соперник играет разумно, то осторожность поведения мотивирует выбор игроком А одной из своих максиминных стратегий, а игроком В - одной из своих минимаксных стратегий. В этом случае игрок А обеспечивает себе выигрыш, не меньший нижней цены игры , а игрок В гарантирует, что выигрыш игрока А будет не больше верхней цены игры .

Стратегия игрока» состоящая в случайном выборе одной из его чистых стратегий, называется смешанной стратегией. Таким образом, смешанная стратегия игрока представляет собой дискретную случайную величину, значениями которой являются номера его чистых стратегий.

При условии, что множество чистых стратегий игрока А известно, каждая его смешанная стратегия Р определяется вероятностями с которыми выбираются игроком А соответствующие чистые стратегии. Поэтому смешанную стратегию Р можно отождествить с -мерным вектором ,т.е.

.

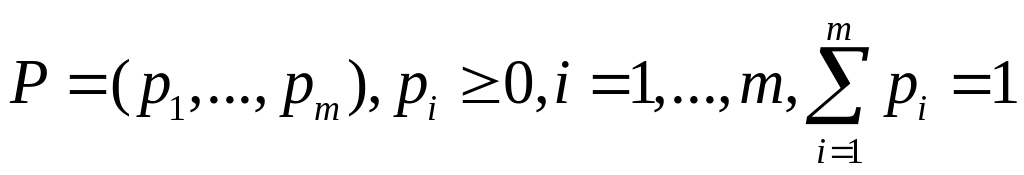То же относится и к смешанным стратегиям игрока B:

.

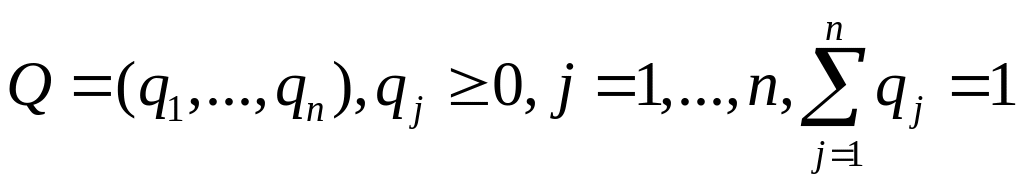Обозначим через

.

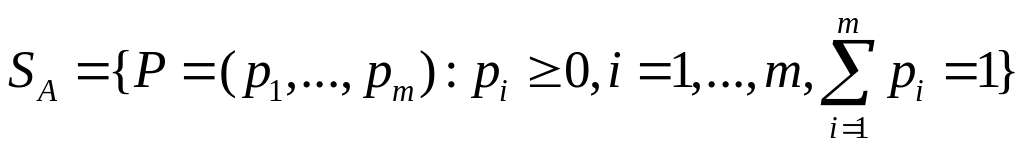Каждую чистую стратегию , игрока А можно рассматривать как смешанную стратегию

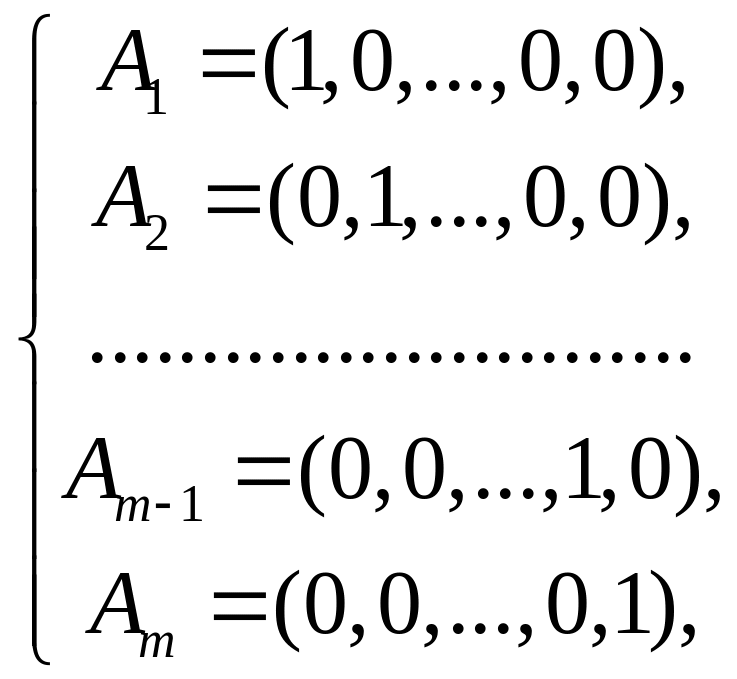(5.1)

Таким образом, каждую смешанную стратегию можно представить линейной комбинацией чистых стратегий с коэффициентами, являющимися координатами данной смешанной стратегии:

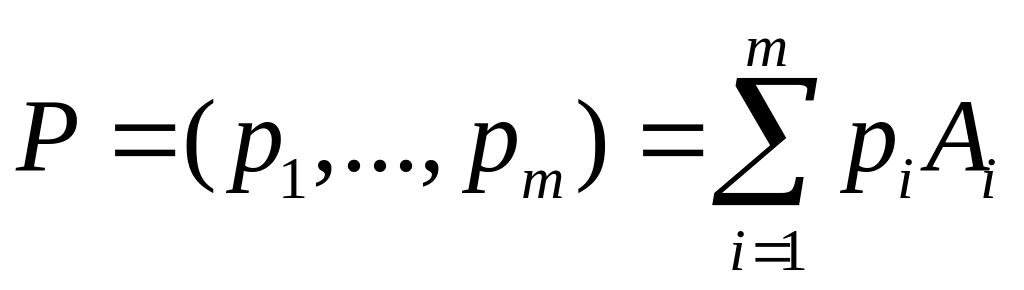. (5.2)

Представления (5.1) и (5.2) дают возможность геометрически проинтерпретировать конфигурацию множеств и чистых и смешанных стратегий соответственно.

Руководствуясь приведенными определениями, мы видим, что правая часть равенства (у.2) является выпуклой комбинацией орт (см. (5.1)) и потому множество всех смешанных стратегий геометрически представляет собой фундаментальный -мерный симплекс с вершинами в точках , представляющих чистые стратегии (выпуклая оболочка, натянутая на чистые стратегии).

Примеры симплексов

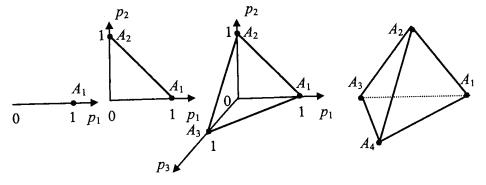
Тема 6. Функции выигрыша в смешанных стратегиях

Если игроки А и В независимо друг от друга выбрали смешанные стратегии соответственно и , то упорядоченная пара (Р, Q) называется ситуацией в смешанных стратегиях. В условиях ситуации (Р, Q) в смешанных стратегиях чистые стратегии и выбираются независимо друг от друга случайным образом с вероятностями соответственно и . Поэтому вероятность совместного выбора чистых стратегий равна произведению их вероятностей: . Но в ситуации в чистых стратегиях игрок А получает выигрыш . Вероятность этого выигрыша совпадает с вероятностью ситуации , т. е. равна .

Таким образом, выигрыш игрока А в ситуации (Р, Q) в смешанных стратегиях представляет собой дискретную случайную величину, принимающую значения с вероятностью . Тогда средний выигрыш игрока А в ситуации (Р, Q) в смешанных стратегиях есть математическое ожидание указанной случайной величины

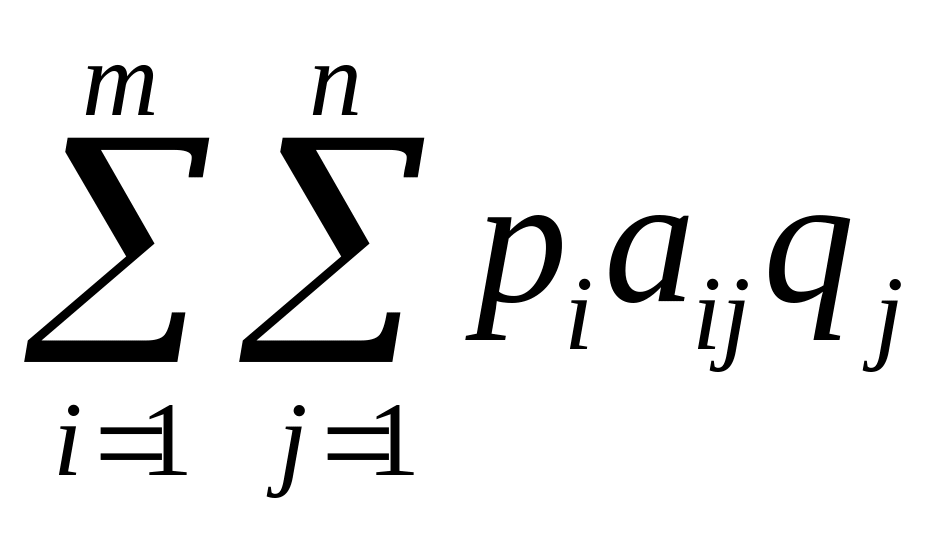(6.1)

Определим функцию выигрыша игрока А в смешанных стратегиях как функцию H, заданную на декартовом произведении множеств смешанных стратегий, ставящую в соответствие каждой ситуации в смешанных стратегиях средний выигрыш игрока А в этой ситуации, определяемый выражением (8.1). Таким образом,

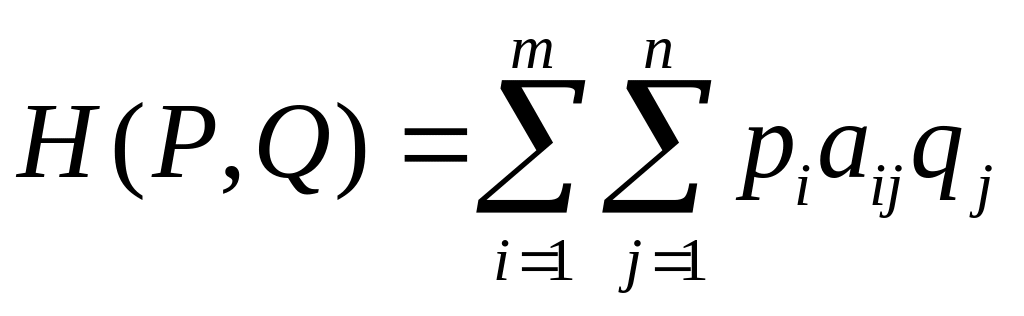, , (6.2)

где , .

Форма (6.2) задания функции выигрыша в смешанных стратегиях называется координатной. Функцию Н можно задать и в матричной форме

,

Теорема 6.1. Для каждой смешанной (в частности, чистой) стратегии игрока А существует (достигается)

(6.2)

Для каждой смешанной (в частности, чистой) стратегии е8_в игрока В существует (достигается)

(6.3)

Число , определенное равенством (6.2) (существование которого доказано в теореме 6.1), назовем показателем эффективности смешанной стратегии игрока А относительно множества смешанных стратегий игрока В.

Если в этом определении множество смешанных стратегий игрока В заменить на множество его чистых стратегий, то получим определение показателя эффективности смешанной стратегии игрока А относительно множества чистых стратегий игрока В:

. (6.4)

Теорема 6.2. Показатели эффективности любой смешанной (в частности, чистой) стратегии игрока А относительно множеств и чистых и смешанных стратегий противника В равны, т.е.

(6.5)

Число , определенное равенством (6.3), назовем показателем неэффективности смешанной стратегии игрока В относительно множества смешанных стратегий игрока А, а число

(6.6)

показателем неэффективности смешанной стратегии Q игрока В относительно множества чистых стратегий игрока А.

Теорема 6.3. Показатели неэффективности любой смешанной (в частности, чистой) стратегии игрока В относительно множеств и чистых и смешанных стратегий игрока А равны, т.е.

Нижней ценой (или максимином) матричной игры в смешанных стратегиях называется величина

Верхней ценой (или минимаксом) матричной игры в смешанных стратегиях называется величина

Те о р е м а 6.4. Для любой конечной матричной игры существуют нижняя и верхняя цены игры в смешанных стратегиях.

Соотношения между нижними и верхними ценами игры в чистых и смешанных стратегиях устанавливаются в следующей теореме.

Теорема 6.5. Нижняя цена игры а и верхняя цена игры (3 в чистых стратегиях, нижняя цена игры V и верхняя цена игры

в смешанных стратегиях удовлетворяют следующему неравенству

.