3.2. Элементы теории автоматов

Ранее упоминалось, что дискретные устройства делятся на комбинационные и последовательностные. Поведение дискретных последовательностных устройств описывается математической моделью, называемой автоматом.

Автомат – это пятерка объектов <X, Q, Y, ψ, φ>, где X – входной алфавит; Y – выходной алфавит; Q – внутренний алфавит или множество состояний автомата; ψ – функция переходов; φ – функция выходов.

Функция ψ определяется на множестве X´Q и принимает значения на множестве Q:

ψ: X´Q ® Q.

Функция φ также определяется на множестве X´Q и принимает значения на множестве Y:

φ: X´Q ® Y.

Будем считать, что алфавиты X, Q, Y конечны.

Напомним, что дискретные устройства функционируют в дискретные моменты (такты) времени t = 1, 2, 3,… Если в момент времени t устройство находится в состоянии q(t), q(t) Î Q и на него поступает входное воздействие x(t), x(t) Î X, то на выходе устройства появляется реакция y(t) = φ(x(t), q(t)), y(t) Î Y и устройство переходит в состояние q(t + 1) = ψ(x(t), q(t)).

3.2.1. Классификация автоматов

Автомат А = <X, Q, Y, φ, ψ> называется полностью определенным, если его функции φ, ψ определены на всех элементах декартова произведения X´Q. Если эти функции определены не на всех элементах этого декартова произведения, то автомат называется частичным или не полностью определенным. Соответствующий введенному ранее определению автомат называется автоматом Мили.

Автомат А называется автоматом Мура, если его функция выхода не зависит от символов входного алфавита, то есть его функции переходов, выходов имеют вид

ψ : X´Q ® Q,

φ: Q ® Y.

Автомат А называется автоматом состояний или автоматом без выхода, если для него φ = ψ и Y = Q. Автомат без выхода рассматривается как тройка объектов <X, Q, ψ>.

Приведенная выше классификация автоматов связана с ограничениями, накладываемыми на функции переходов, выходов автомата А. Далее перейдем к классификации, связанной с ограничениями, накладываемыми на мощности алфавитов.

Автомат с одноэлементным входным алфавитом, |X| = 1, называется автономным автоматом. Ему сопоставляются функции переходов, выходов следующего вида:

ψ : Q ® Q,

φ : Q ® Y.

Имея в виду, что соответствующие автоматам дискретные устройства функционируют в дискретные моменты времени, перепишем функции переходов, выходов в виде

y(t) = φ (q(t)),

q(t + 1) = ψ(q(t)), t = 1, 2, 3,…

Пусть начальное состояние автомата 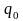= q(1), тогда в случае полностью определенных функций переходов и выходов автомат реализует единственную последовательность внутренних состояний:

q(1), q(2), q(3),…

и соответствующую ей последовательность выходных состояний:

y(1), y(2), y(3),…

В силу конечности алфавита Q в последовательности q(1), q(2),…, q(k + +1), где k – мощность алфавита Q, найдутся повторяющиеся символы, первый повторяющийся символ является началом периодической (циклической) последовательности. Из сказанного следует, что как последовательность внутренних состояний, так и выходная последовательность являются периодическими с длиной периода не более k, в общем случае с некоторым предпериодом.

Итак, полностью определенный автономный автомат является математической моделью генератора периодической последовательности y(1), y(2),…

Автомат с одноэлементным внутренним алфавитом, |Q| = 1, называется комбинационным автоматом или автоматом без памяти. Он обозначается <X, Y, φ>. Последнее название автомата имеет следующую семантику. Обычно величину 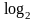|Q| называют объемом памяти автомата, для комбинационного автомата эта величина равна 0.