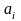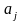- •Глава 3. Анализ и синтез дискретных систем
- •3.1. Применение теории днф к синтезу комбинационных логических сетей (комбинационных схем)
- •3.1.1. Логические элементы
- •3.1.2. Комбинационные логические сети
- •3.1.2.1. Задача анализа
- •3.1.2.2. Синтез в базисе днф
- •3.1.2.3. Синтез в базисе не и
- •3.1.2.4. Синтез в базисе не или
- •3.2. Элементы теории автоматов
- •3.2.1. Классификация автоматов
- •3.2.2. Способы задания конечных автоматов
- •3.2.3. Триггеры
- •3.2.4. Канонические уравнения
- •3.2.5. Автоматы и языки
- •3.2.6. Операции над конечноавтоматными языками
- •Глава 4. Алфавитное кодирование
- •4.1. Критерий однозначности кодирования
- •4.2. Алгоритм распознавания однозначности кодирования
- •4.3. Свойства однозначных кодов
- •4.4. Коды с минимальной избыточностью
- •Глава 5. Исчисление высказываний и исчисление предикатов
- •5.1. Исчисление высказываний
- •5.1.1. Словарь исчисления высказываний
- •5.1.2. Синтаксис исчисления высказываний
- •5.1.3. Семантика исчисления высказываний
- •5.1.4. Исчисление высказываний и естественный язык
- •5.1.5. Выполнимость и общезначимость формулы
- •5.1.6. Проблема выводимости
- •5.1.7. Алгоритмы распознавания невыполнимости формулы
- •5.1.8. Хорновские дизъюнкты
- •5.2. Исчисление предикатов
- •5.2.1. Словарь
- •5.2.2. Синтаксис исчисления предикатов
- •5.2.3. Семантика исчисления предикатов
4.4. Коды с минимальной избыточностью
Задан
алфавит А
= {
,…,
},
r
2, и набор вероятностей
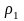 ,…,
,…,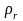 (
(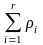 =
1 ) появления символов
,…,
.
Задан также алфавит В
= {
,…,
},
q
2. Можно построить различные алфавитные
кодирования, обладающие свойством
однозначности.
=
1 ) появления символов
,…,
.
Задан также алфавит В
= {
,…,
},
q
2. Можно построить различные алфавитные
кодирования, обладающие свойством
однозначности.
Для
каждой схемы кодирования Σ введем
величину
 ,
называемую избыточностью кодирования.
Она определяется как математическое
ожидание длины элементарного кода:
,
называемую избыточностью кодирования.
Она определяется как математическое
ожидание длины элементарного кода:
=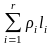 ,
=
l(
),
>
1.
,
=
l(
),
>
1.
Введенная величина показывает, во сколько раз увеличивается длина слова при кодировании, заданном схемой Σ.
Рассмотрим пример: r = 4, q = 2,
= 0,4,
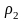 =
0,25,
=
0,25,
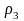 =
0,2,
=
0,2,
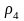 =
0,15.
=
0,15.
Заданы
две схемы кодирования
,
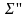 .
.
:
|
00 |
|
01 |
|
10 |
|
11 |
:
|
1 |
|
01 |
|
000 |
|
001 |
Обе
схемы обладают свойством однозначности,
но характеризуются разной избыточностью:
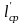 =
2,
=
2,
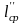 =
0,4 + 2*0,25 + 3*0,35 = 1,95.
=
0,4 + 2*0,25 + 3*0,35 = 1,95.
Пусть
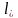 =
min
.
=
min
.
Определение. Коды, для которых = , называются кодами с минимальной избыточностью или кодами Хафмана.
Эти коды в среднем дают минимальное увеличение длин слов при кодировании.
Рассмотрим задачу построения кода с минимальной избыточностью.
Известно, что для всякой однозначной схемы кодирования существует однозначная схема кодирования со свойством префикса (теорема 4.5) и с тем же самым значением . Поэтому в дальнейшем ограничимся рассмотрением только кодов со свойством префикса.
Каждому алфавитному кодированию со свойством префикса можно сопоставить кодовое дерево. Покажем его построение на примере.
Пусть r = 8, q = 4, схема Σ и сопоставляемые кодам вероятности имеют вид
|
|
= 0,22 |
|
|
= 0,2 |
|
|
= 0,14 |
|
|
= 0,11 |
|
|
|
|
|
|
|
|
|
|
|
|
= 0,2 + 2 (0,22 + 0,14 + 0,11 + 0,09 + 0,08) + 3 (0,1 + 0,06) =
= 0,2 + 2*0,064 + 3*0,16 = 0,2 + 1,28 + 0,48 = 1,96.
Концевым вершинам дерева рис.4.2 соответствуют элементарные коды, определяемые простыми цепями, соединяющими корень с листьями дерева. Ребра первого яруса дерева отмечаются первыми символами элементарных кодов, ребра второго яруса – вторыми символами и т.д. Листьям дерева приписываются вероятности появления элементарных кодов. Дерево рис. 4.2 задает схему алфавитного кодирования со свойством префикса.
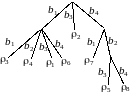
Без ограничения общности будем считать:
… .
Теорема
4.6. Для кода
с минимальной избыточностью из условия
 <
<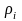 следует, что
следует, что
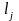
.
.
Доказательство. Предположим противное: < и < .Тогда, если в схеме Σ:
… |
… |
|
|
… |
… |
|
|
… |
… |
поменять местами коды , , то получим схему :
… |
… |
|
|
… |
… |
|
|
… |
… |
имеющую меньшую избыточность , чем . В самом деле,
– = ( + ) – ( + ) = ( – )( – ) > 0.
Это противоречит условию минимальной избыточности схемы кодирования Σ. Ч.Т.Д.
Следствие.
В кодовом дереве для кода с минимальной
избыточностью вероятности, приписываемые
вершинам яруса
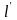 ,
не меньше вероятностей, приписываемых
вершинам яруса
,
не меньше вероятностей, приписываемых
вершинам яруса
 ,
если
>
.
,
если
>
.
Будем рассматривать конечные деревья с максимальным порядком ветвления (числом исходящих из вершин ребер) q.
Определение. Конечное дерево называется насыщенным, если порядки ветвления всех его вершин, за исключением, быть может, одной, лежащей в предпоследнем ярусе, равны 0 или q. Порядок ветвления этой исключительной вершины равен , где 2 q.
Заметим, что определяется однозначно из уравнения
r = t(q – 1) + .
Вычислим остаток от деления r на q – 1 и будем считать:
q – 1, |
если остаток от деления равен 0, |
остатку |
– в противном случае. |
Рассмотрим два преобразования кодового дерева (рис. 4.2).
1. Удаление ребра, исходящего из вершины с порядком ветвления один.
Пусть в кодовом дереве, порожденном схемой Σ, содержится вершина порядка 1, из которой исходит ровно одна дуга, заканчивающаяся концевой вершиной дерева (листом), и пусть концевой вершине приписана вероятность ρ.
a) Удалим это ребро.
b)
Припишем величину ρ вершине, из которой
оно исходило. Получим новое кодовое
дерево, представляющее схему кодирования
 .
.
Новое кодовое дерево имеет меньшую избыточность. (Избыточность схемы кодирования и представляющего ее дерева будем отождествлять.) Действительно, = – ρ.
2. Перемещение ребра в ненасыщенную вершину более близкого к корню яруса по сравнению с вершиной, из которой это ребро исходило, или в вершину того же яруса.
Рассмотрим некоторую вершину дерева кодирования, порожденного схемой Σ, из которой исходит ребро, заканчивающееся в концевой вершине. Концевой вершине приписана величина ρ и соответствует кодовое слово B.
a) Перенесем это ребро вместе с концевой вершиной в ненасыщенную вершину того же яруса или более близкого к корню яруса.
b) Припишем концевой вершине величину ρ. Получим новое кодовое дерево, представляющее схему .
Новое кодовое дерево имеет не большую избыточность. Действительно, при перенесении ребра в ненасыщенную вершину того же яруса избыточность кодового дерева сохраняется. При перенесении ребра в ненасыщенную вершину, расположенную ближе к корню, избыточность нового кодового дерева уменьшается.
Теорема 4.7. Для всякого кода с минимальной избыточностью существует насыщенное дерево, его представляющее.
Доказательство. Преобразования 1, 2 позволяют любое кодовое дерево, в том числе и кодовое дерево, обладающее минимальной избыточностью, привести к насыщенному дереву, не увеличивая при этом избыточности кодового дерева. Ч.Т.Д.
Кодовое дерево рис. 4.2 преобразуется в насыщенное кодовое дерево рис. 4.3.
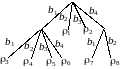
= 0,22 + 0,2 + 2 (0,14 + 0,11 + 0,1 + 0,09 + 0,08 + 0,06) = 0,42 + 2*0,58 = =1,58.
Избыточность кода рис. 4.3 меньше избыточности кода рис. 4.2.
Замечание. При приведении произвольного кодового дерева, представляющего схему кодирования со свойством префикса, к насыщенному дереву, представляющему код с минимальной избыточностью, может оказаться удобным сначала получить насыщенное дерево, не обращая внимания на приписываемые концевым вершинам вероятности, а затем приписать концевым вершинам вероятности с учетом теоремы 4.6. Это может потребовать меньшего количества операций 1, 2, чем соблюдение условий теоремы на этапе получения насыщенного дерева.
Договоримся в насыщенном кодовом дереве концевым вершинам одного и того же яруса приписывать вероятности по невозрастанию слева направо. Такое дерево будем называть приведенным насыщенным деревом.
Теорема 4.8. Для кода с минимальной избыточностью существует приведенное насыщенное дерево.
Доказательство следует из определения приведенного насыщенного дерева.
Введем операцию редукции в приведенном насыщенном дереве.
Выделим
в нем последнюю неконцевую вершину
предпоследнего яруса дерева. Из нее
исходит
ребер, 2
q.
Концевым вершинам этих ребер приписаны
вероятности
 ,…,
,…, ,
…
.
,
…
.
Удалим все ребра, исходящие из рассматриваемой вершины, вершине припишем величину ρ, ρ = + … + .
Получим новое дерево кодирования, такое, что соответствующий ему алфавит A сокращается на – 1 символов.
Теорема 4.9. Операция редукции порождает новое кодовое дерево с минимальной избыточностью.
Доказательство. Если полученное дерево не обладает минимальной избыточностью, то и порождающее его дерево не обладает минимальной избыточностью. Пришли к противоречию. Ч.Т.Д.
Алгоритм построения кода с минимальной избыточностью
Алгоритм основан на применении операции редукции к приведенному насыщенному дереву.
Заданы алфавиты А, В с параметрами r, q и вероятностями ,…, , … . Параметр однозначно определен исходными данными. Многократное выполнение редукции в концеконцов приводит к превращению очередного дерева в пучок порядка .
Анализ результатов операций редукции позволяет получить код с минимальной избыточностью.
Поясним сказанное на примере. Пусть r = 4, q = 2, = 0,4, = 0,25, = 0,2, = 0,15, B = {0, 1}. Выполнив очередную редукцию, в новом алфавите новые вероятности располагаем по невозрастанию:
|
|
|
|
|
|
|
|
|
0,6 |
|
0 |
|
|
|
|||||||||||
|
0,4 |
|
|
|
0,4 |
|
|
|
0,4 |
|
1 |
|
|
||||||||||||
|
|
|
|
|
0,35 |
|
0 |
|
|
|
|
|
|
|
|
|
|
||||||||
|
0,25 |
|
|
|
0,25 |
|
1 |
|
|
|
|
|
|
|
|
|
|||||||||
|
0,2 |
|
0 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||
|
0,15 |
|
1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
В рассматриваемом примере необходимо выполнить три шага, связанные с редукцией. Квадратными скобками отмечены объединяемые члены.
Для построения кодов необходимо для каждой скобки задать соответствие между величинами вероятностей и символами алфавита В, двигаясь, например, слева направо.
Осуществляем движение в обратном направлении к символам ,…, и, проходя скобки, выписываем соответствующий код. Например, путь 0,6 – 0,35 – 0,15 – представляет код 001. В результате получаем следующую схему кодирования:
|
1 |
|
01 |
|
000 |
|
001 |

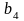
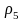 =
0,1
=
0,1
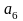
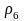 =
0,09
=
0,09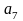
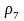 =
0,08
=
0,08
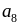
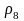 =
0,06
=
0,06