
4.4. Ранг матриці та обернена матриця
Нехай задана матриця А розміру m x n
Виберемо в ній довільно k рядків та k стовпців. Елементи, що знаходяться на перетині виділених рядків та стовпців, утворюють квадратну матрицю k-того порядку, визначник якої називають мінором k-того порядку матриці А. Обираючи різними способами k порядків та k стовпців, одержимо деяку кількість мінорів k-того порядку. Матриця має мінори будь-якого порядку: від першого (елементи матриці-мінори 1-го порядку) до найменшого із чисел m та n.
Розглянемо в матриці А ті її мінори різних порядків, які відмінні від нуля і нехай їх найбільший порядок дорівнює г.
Означення 1. Рангом матриці називають найбільший порядок її мінорів, відмінних від нуля.
Ранг матриці позначають г (А) або ід або просто гА. Ранг матриці можна знаходити методом обвідних мінорів або простіше – методом елементарних перетворень.
Означення 2. Елементарними перетвореннями матриці називають наступні перетворення:
1) перестановка рядків (стовпців) матриці;
2)
множення всіх елементів рядка (стовпця)
на число
![]() ;
;
3) додавання до елементів рядка (стовпця) відповідних елементів іншого рядка (стовпця), помножених на деяке число.
Всі ці перетворення не змінюють ранг матриці, але з їх допомогою матрицю зводять до матриці, у якої нижче головної діагоналі всі елементи – нулі. Тоді ранг матриці дорівнює кількості елементів головної діагоналі, відмінних від нуля.
Приклад 1. Знайти ранг матриць:
 b)
b)
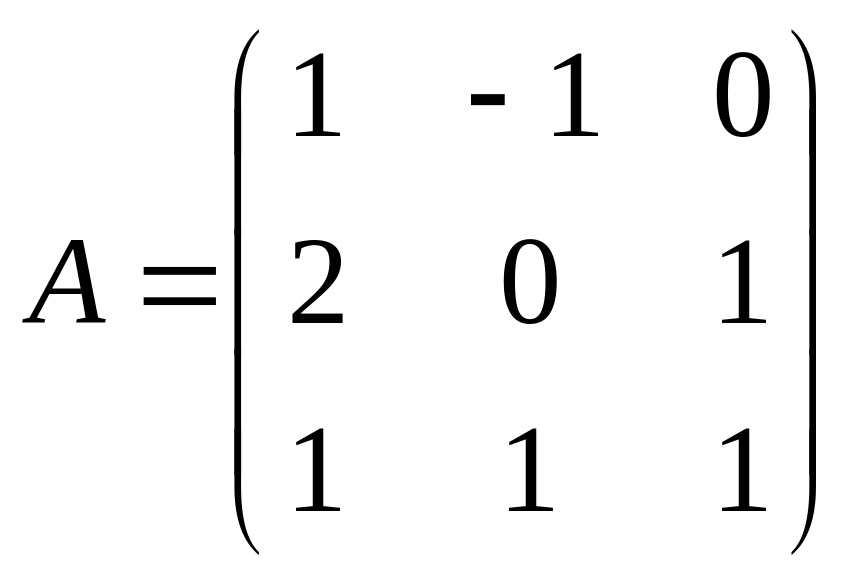
c)
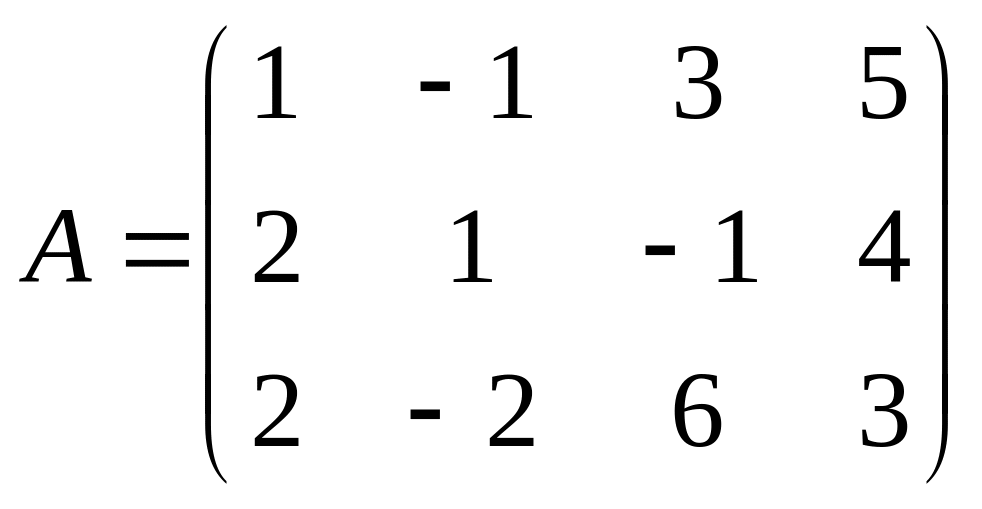 d)
d)
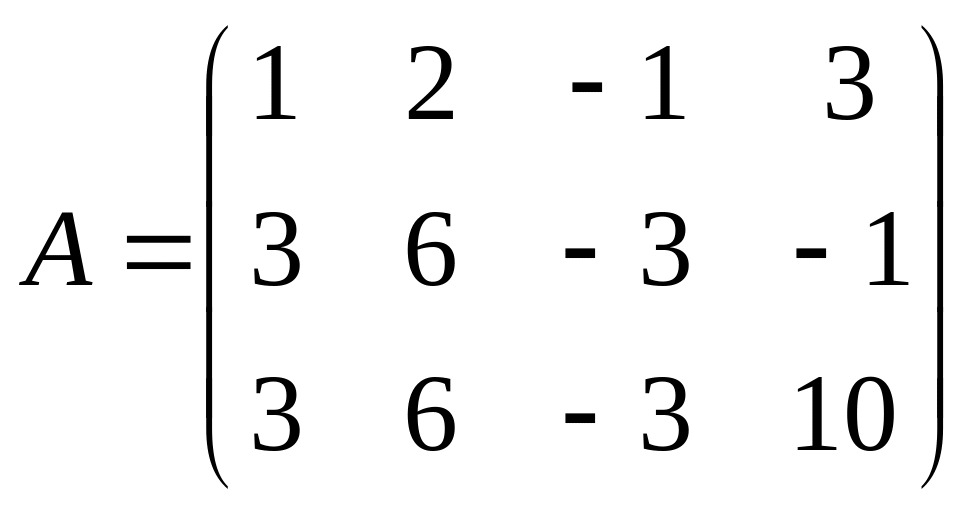
Розв'язування. Ранг матриць будемо знаходити методом елементарних перетворень.
a) Елементи першого рядка матриці помножимо на (-3) і додамо до відповідних елементів другого рядка матриці А:
![]() .
.
Звідси випливає, що ранг цієї матриці дорівнює 1 (нижче головної діагоналі – нуль та один елемент головної діагоналі 0)
b) Зробимо такі перетворення, щоб нижче головної діагоналі були нулі:
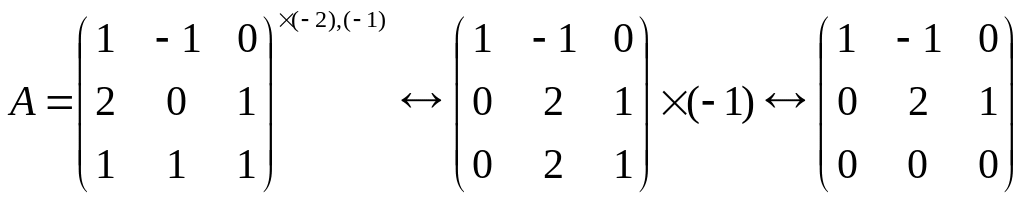 .
.
Звідси випливає, що г(А) = 2.
Знову робимо такі перетворення, щоб нижче головної діагоналі були нулі:
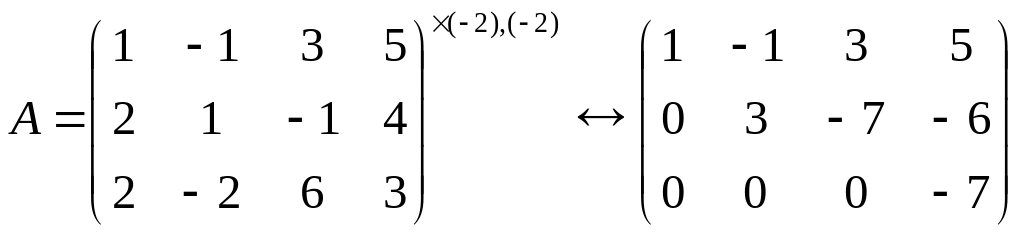 .
.
Оскільки можна третій та четвертий стовпці поміняти місцями і отримати третій елемент головної діагоналі, який 0, то г(А)=3.
Перетворимо матрицю аналогічно попередньому
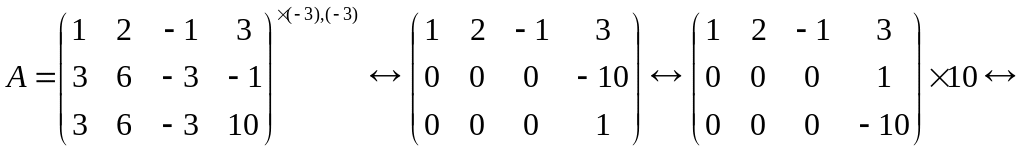
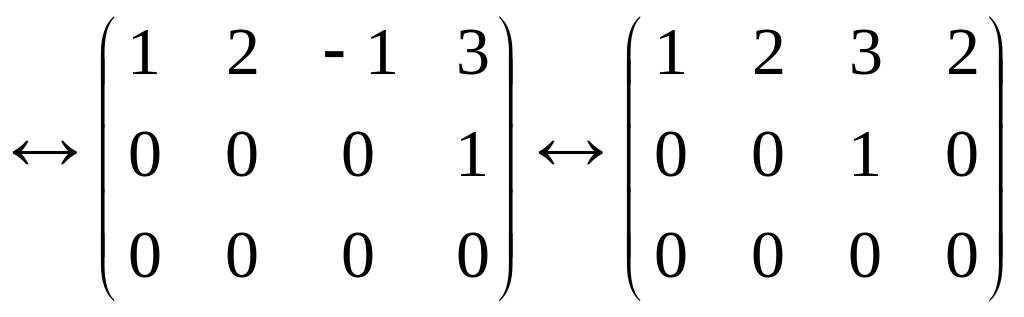 .
.
Звідси випливає, що г(А) = 2.
Означення 3. Матриця А-1 називається оберненою матрицею до матриці А, якщо виконуються рівності
AA-1=A-1A=E (1)
тобто матриці А та А-1 комутують і їх добуток є одинична матриця.
Не всяка матриця має обернену. В алгебрі матриць доведено, що матриця А має обернену матрицю А-1 при виконанні двох умов:
1) матриця А квадратна;
2) визначник |А| матриці А не дорівнює нулю.
Обернену матрицю А-1 до матриці А можна знаходити двома способами:
за формулою
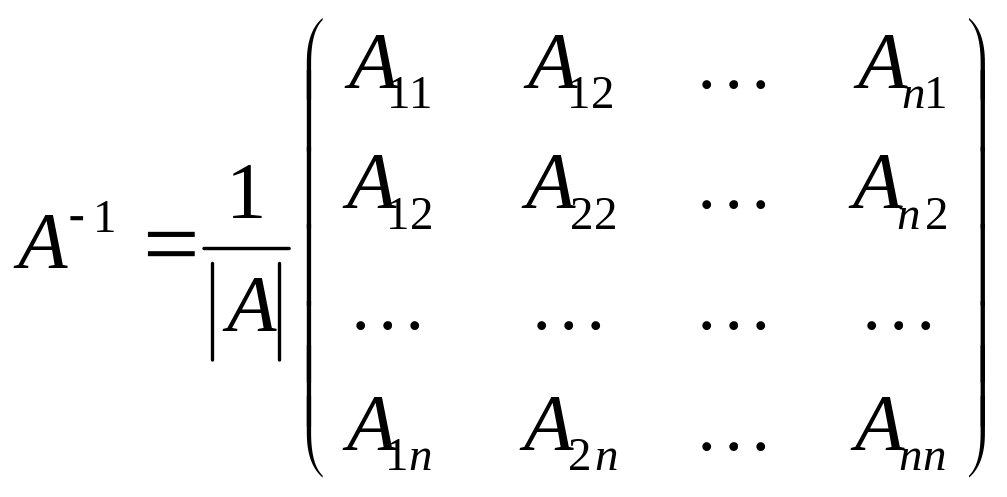
де Аij – алгебраїчні доповнення елементів аij матриці А, (алгебраїчні доповнення до і-го рядка розташовані у і стовпці (і=1,2,..,п)), а також з використанням означення оберненої матриці – та елементарних перетворень матриць.
Приклад 2. Знайти обернену матрицю до матриці
 .
.
Розв'язування. Спочатку впевнимося що матриця А має обернену А-1.
Матриця А має три рядки та три стовпці, тому вона квадратна порядку 3. Її визначник
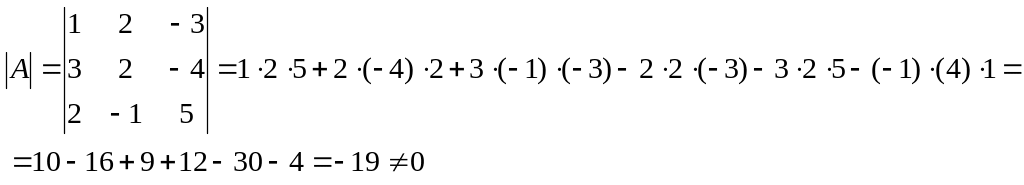 Отже,
матриця А має обернену А-1,
яку знайдемо за формулою (2).
У даному випадку алгебраїчними
доповненнями до елементів матриці А
будуть:
Отже,
матриця А має обернену А-1,
яку знайдемо за формулою (2).
У даному випадку алгебраїчними
доповненнями до елементів матриці А
будуть:
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() ;
;
![]() .
.
Таким чином, одержали
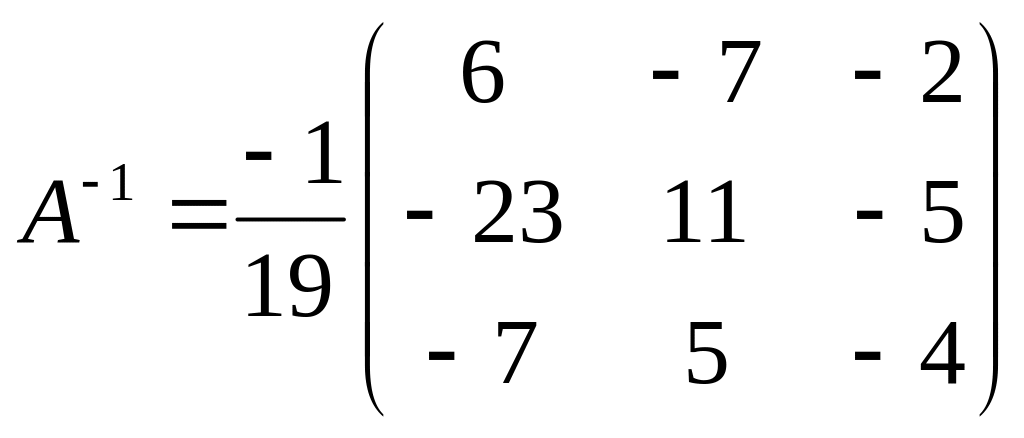 .
.
Приклад З. Знайти обернену матрицю до матриці
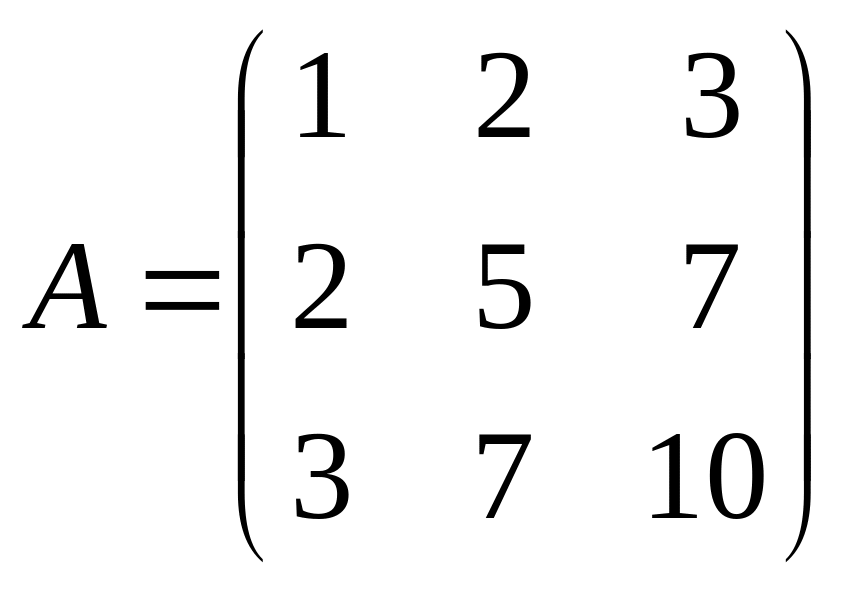
Розв’язування. Задана матриця А квадратна порядку 3, її визначник:
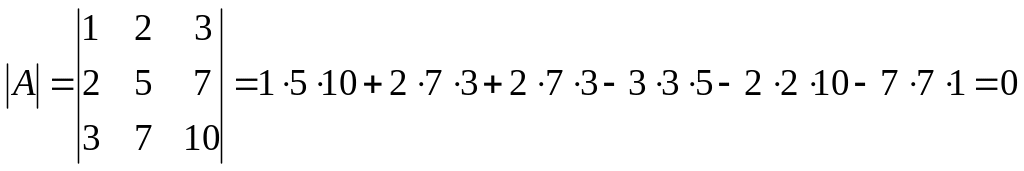
Отже, ця матриця оберненої не має.
Зауваження. Якщо матриця А квадратна другого порядку
![]() ,
визначник якої |А|
0, то обернену до неї матрицю А-1
можна знайти за формулою
,
визначник якої |А|
0, то обернену до неї матрицю А-1
можна знайти за формулою
![]() (3)
(3)
тобто треба елементи головної діагоналі матриці А поміняти місцями, елементи неголовної діагоналі помножити на (-1) і одержану матрицю помножити на 1/|А|.
Приклад
4.
Знайти обернену матрицю до матриці
![]() .
.
Розв’язування. Задана квадратна матриця другого порядку, її визначник
![]()
тому для знаходження А-1 можна застосувати формулу (3). Одержимо:
![]() .
.
Приклад 5. (Модель міжгалузевого планування потреб та пропозицій). Таблицею задані показники взаємних потреб та пропозицій між різними галузями промисловості.
-
Галузеві
Галузеві потреби
Потреби
Кількість
пропозиції
1
2
3
інших галузей
усіх пропозицій
1
20
48
18
14
100
2
30
12
54
24
120
3
30
36
36
72
180
Витрати праці
20
24
72
a) Визначити матрицю потреб-пропозицій А;
b) Припустимо, що через три роки потреби інших галузей зростуть до 24, 33 та 75 показників для галузей 1, 2, 3, відповідно. Скільки продукції повинна виробити кожна галузь, щоб задовольнити ці потреби?
Розв'язування. а) Елементи шуканої матриці А дорівнюють відношенню потреб і-тої галузі до загальної кількості пропозицій цієї галузі. Тому для знаходження елементів і-го стовпця (і = 1, 2, 3) матриці А треба поділити потреби і-тої галузі, вказані у таблиці, на загальну кількість пропозицій цієї галузі.
