Аппроксимация функций с помощью алгебраических интерполяционных

полиномов

С их помощью аппроксимируют не сложные функциональные зависимости.

Полином Лагранжа. Интерполяционный многочлен Лагранжа.

Требуется найти полином n-ой степени который в N точках совпадает со значением функции f(x).

Для этого предварительно составим систему полиномов {φ_i(x)} каждый из которых в т. x _j равен единице, а в остальных точках равен 0. Тогда искомый интерполяционный полином будет иметь вид: (4)

Набор функций {φ_i(x)} - фундаментальная система полинома (базисные многочлены степени n).

По определению(чтобы многочлен был интерполяционным):

полиномы φ_j(x_k) должны удовлетворять условию:1. при j=k обращаются в 1, 2. при j k - в 0, следовательно их можно представить в виде : (5),

а коэффициент сj легко получается из условия для интерполяции φ_j(x_k)=1 , подставляя в выражение (5) значение x=x_k и приравнивая его единице, получим ,

тогда базисные многочлены Лагранжа

j=0,1,2,…N (6)

А искомый интерполяционный полином Лагранжа имеет вид:

(7)

Это выражение представим в более компактной форме. Для этого введем вспомогательную функцию :

(8),

Если умножить и разделить каждое из слагаемых выражения (7) на (х – х_j) и заменить числитель на П_n+1(х), а знаменатель на П_n+1^/(х_j) (это производная функции П(х) в j-ом узле, равная ), то получим формулу полинома Лагранжа в общеизвестном виде :

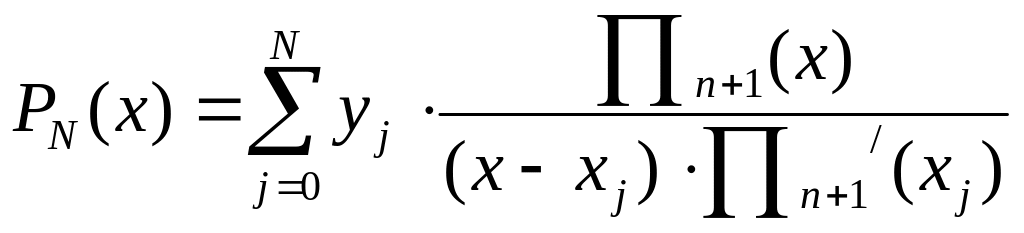(9)

Пример: рассмотрим построение интерполяционного полинома Лагранжа, аппроксимируя основную кривую намагничивания аморфной стали марки 7421, отожженной в магнитном поле.

Необходимость аппроксимации функции В = f(H) возникает при расчете устройств силовой электроники, содержащих ферромагнитные элементы (трансформаторы, электрические машины ...).

Рис.1

Для аппроксимации функции В = f(H) (рис. 1) с помощью интерполяционного полинома Лагранжа 3 (кубическая интерполяция) степени необходимо иметь значение этой функции в 4 точках (т. О, А, В, С ).

Полиномы 1 и 2-ой степени, называются линейной и квадратичной интерполяцией соответственно.

Согласно формуле (7) интерполяционный полином Лагранжа имеет вид :

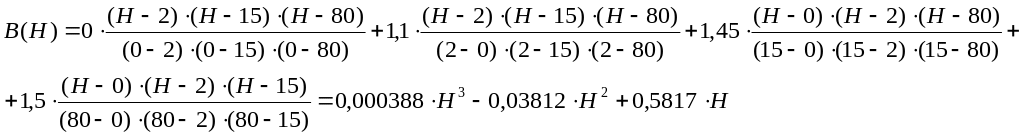
В точке H_j значения полинома равны экспериментальным данным. В остальных точках погрешность аппроксимации достигает неприемлемых размеров, см. рис. 2, где (*) помечены значения индукции В, полученные подстановкой различных величин в [интерполяционный полином (7).

Рис.2

На первый взгляд может показаться, что точность аппроксимации можно повысить за счет увеличения узловых точек N, но исследования показали, что при N→∞ последовательность полиномов P_n(x) не всегда сходится к f(x).

Практикой установлено, что эффективность полиномов Лагранжа увеличивается при интерполяции гладких функций и число N является небольшим. В математическом обеспечение ЭВМ имеются стандартные программы аппроксимации, в которых реализована формула Лагранжа при малых N (часто N=4). Использование интерполяционной формулы Лагранжа для обработки экспериментальных данных требует учета ошибок эксперимента.

Формула Лагранжа при N≥4 становится громоздкой для практического использования, т. к. в нее входит произведение П(х).

Погрешность интерполяционной формулы Лагранжа.

Значения полинома Лагранжа используются для аппроксимации функции f(x), поэтому правомочен вопрос: на какую величину полином P_n(x) отличается от f(x) в точке, не соответствующей узловым точкам.

Обозначим остаточный член интерполяции в виде R_n(x) = f(x)-P_n(x). Остаточный член интерполяции можно оценить теоретически в том случае, если функция f(x) n+1 раз дифференцируема.

Если известна величина (10),

то оценить абсолютную погрешность интерполяционной формулы в любой точке отрезка интерполяции можно с помощью неравенства

(11*)

А максимальная погрешность интерполирования на отрезке оценивается величиной

. (12)

Пример: Оценить погрешность приближения функции в точке x= 116 и на всем отрезке , где a=100, b=144, с помощью интерполяционного многочлена Лагранжа второй степени, построенного с узлами =100, =121, =144

, , ,

На основании формулы (11*) получаем

В силу оценки (12) получаем .

Самостоятельно можно проверить, что погрешность аналитического решения будет меньше погрешности (11*), которая в свою очередь будет меньше погрешности (12).

Минимизация погрешности многочленной интерполяции путем специального выбора узлов интерполяции.

Если выбрать узлы интерполяции определённым образом, то можно уменьшить абсолютную погрешность интерполирования. Выберем в качестве узлов интерполяции нули многочлена (полинома) Чебышева 1-го рода.

Tn(x)=cos[n(arccosx)] (13)

Где n - порядок полинома. Доказательство, что данная функция является многочленом, можно найти в учебной литературе по курсу.

полином II –го рода (14)

Из уравнения Т_N(x)=0 если считать, что функция y=f(x) задана на [-1;1], то получим:

j=0…N (15)

Т.к. узлами интерполяции служат нули полинома Т_n(х), то можно функцию П(х) заменить на T_N(x).

-1≤x≤1 (16)

j=1,2,…,N (17)

С учетом выражений (15 - 17) интерполяционный полином Лагранжа имеет вид:

(18)

-1≤x≤1 x≠x_j

Pn(x_j)=y_j j=0,1,2,…,N - в узлах интерполяции.

Расширим область задания функции y=f(x) на произвольный отрезок [а,b]. Введем замену независимой переменной x = φ₁(u) таким образом чтобы функция

y=f(φ₁(u))=f₁(u) [-1;1].

Пусть функция x=φ₁(u) имеет обратную функцию и точкам x_j соответствуют точки u_j, являющиеся нулями полинома Чебышева I рода. При этом для аппроксимации функции y=f₁(u) можно использовать формулу (23).

Если cчитать

, следовательно функция y аппроксимирует функцию f(x) и очевидно, что преобразование независимой переменной позволяет функцию, заданную на [а,b] свести к функции на отрезке [-1;1].

А преобразование (19)

дает возможность осуществить обратный переход.

Поэтому функцию, заданную на [а,b] можно аппроксимировать с помощью интерполяционного полинома следующего вида:

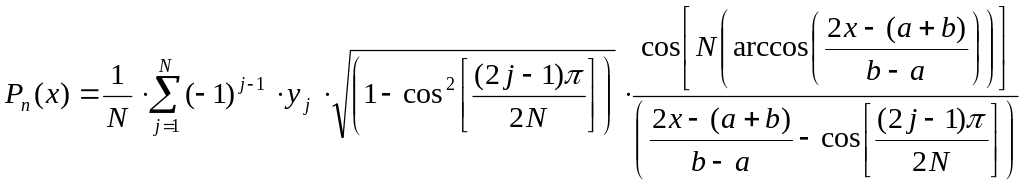x≠x_j (20)

P_n(x_j)=y_j – значение функции в точке.

Узлы интерполяции надо выбирать

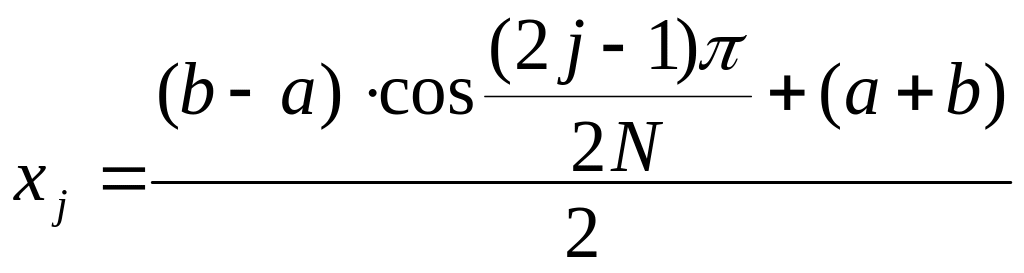j=1,2,…,N (21)

Пример: По формуле (21) определим узлы интерполяции x_j для рассмотренного примера аппроксимации кривой намагничивания аморфной стали В = f(H).

При N = 4, а = 0, b = 80.

По формуле (21) получим:

x₀=76,95 y₀=1,498 эти точки – новые

x₁=55,31 y₁=1,481 узлы интерполяционной

x₂=24,69 y₂=1,457 формулы Лагранжа

x₃=3,05 y₃=1,205

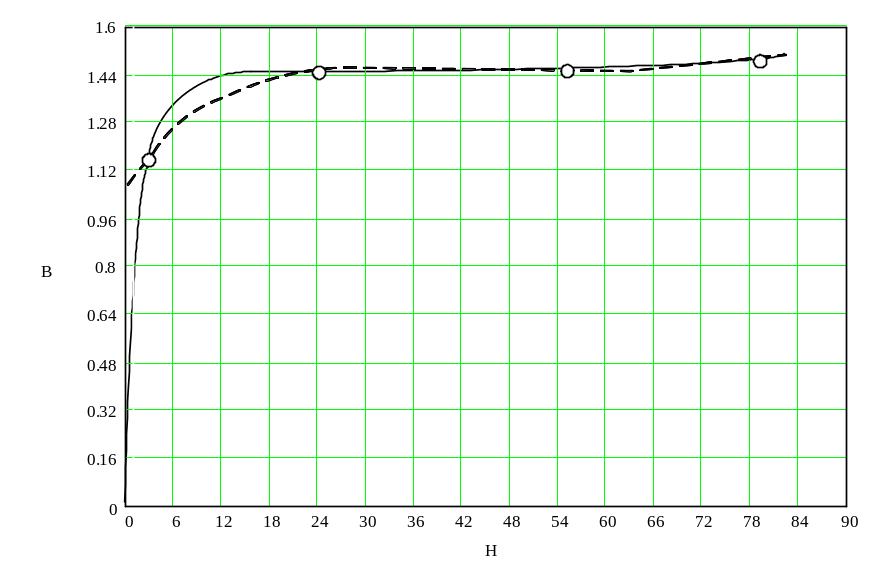
Рис.3

Расчеты, выполненные по (20) для отдельных значений аргумента показаны на рис.3 штрихпунктирной кривой.

При выборе в качестве узлов интерполяции нулей полинома Чебышева 1-го рода, мы можем уточнить величину максимального остаточного члена.

(22)

ВЫВОД: Выбор узлов интерполяции в соответствии с нулями полинома а 1-го рода при сохранение формулы Лагранжа позволила резко увеличить точность аппроксимации. В формуле Лагранжа произведение П(х) следует заменить на тригонометрический полином Чебышева 1-го рода.

Аппроксимация экспериментальных данных с помощью интерполяционной формулы Ньютона.

Рассмотрим другой способ построения интерполяционном многочлена. При этом, однако, не следует забывать, что по заданной таблице, содержащей значения функции в n+ 1 узлов, интерполяционный многочлен п-ой степени единственен, и поэтому «новые» интерполяционные многочлены отличаются от построенного по той таблице многочлена Лагранжа лишь внешним видом.

Тем не менее, они представляют ценность, поскольку вид (т.е. форма записи) многочлена определяет порядок и объем вычислений, что в численных методах существенно.

Для аппроксимации функции часто применяется интерполяционный полином Ньютона. Он строится как для равноотстоящих узлов интерполяции, так и для равноотстоящих, в первом варианте мы будем использовать понятия конечных разностей, а во втором разделенных разностей.

Он содержит разности различных порядков, найденные по значениям функции y₀…y_N в точках x₀,…, x_n.

Разделенные разности первого порядка:

(1)

Разделенные разности второго порядка определяются через разности первого порядка:

(2)

В общем случае разности n порядка можно вычислить по формуле, если вычислить разность N-1 порядка.

(3)

Разделённые разности обычно располагаются в специальной таблице, которая строится по следующей схеме.

x0 y0

f(x0,x1)

x1 y1 f(x0,x1,x2)

f(x1,x2) f(x0,x1,x2,x3)

x2 y2 f(x1,x2,x3) f(x0,x1,x2,x3,x4)

f(x2,x3) f(x1,x2,x3,x4)

x3 y3 f(x2,x3,x4)

f(x3,x4)

x4 y4

Построим интерполяционный полином Ньютона.

Пусть функция f(x) определена на [а, b], а величина х - произвольная точка этого отрезка. Рассмотрим разность первого порядка.

(4)

Из формулы (4) определим значение f(x) в точке .

(5)

Разность второго порядка:

(6)

Из (6) имеем:

(7)

Подставим выражение из формулы (7) в (5)

(8)

Продолжая процесс подстановки получим выражение:

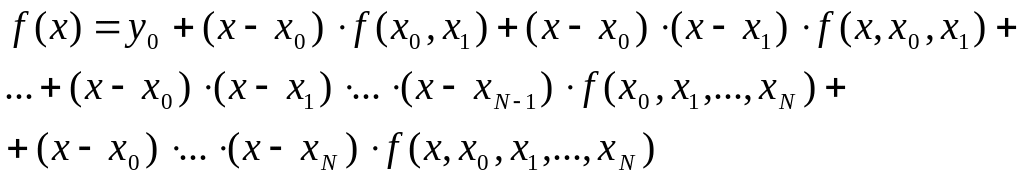(9)

Выражение (9) перепишем в следующем виде

f(x)=P_N (x)+R_N (x) (10)

R_N(x) – остаточный член.

Если f(x) это многочлен степени n, то процесс подобного разложения исчерпывается. Разложение будет состоять из n+1 слагаемого, и все они будут иметь конкретные коэффициенты, так как последняя, содержащая x разделенная разность в (9) имеет (n+1) порядок и, значит, равна нулю. Таким образом, для любого многочлена степени n справедливо тождество

(11)

Полином P_n (x) - является интерполяционным т.к. имеет место равенство:

f(x_j) = P_N (x_j) j=0...N (12)

Этот полином P_n (x) - интерполяционный полином Ньютона для интерполирования вперед, a R_n (x) - остаточный член формулы Ньютона, причем R_n (x) - погрешность метода интерполирования.

R_N (x)=(x-x₀)…(x-x_N)f(x, x₀,x₁,…,x_N)= f(x, x₀,x₁,…,x_N)П_n+1(x), где

П_n+1(x) – многочлен, введенный ранее.

Если известно что функция f(x) N+1 раз дифференцируемая то остаточный член можно оценить:

(13)

А весь остаточный член равен:

(14)

При построении интерполяционного полинома Ньютона порядок расположения узлов интерполяции не играет роли, поэтому (11) перепишем:

(15)

Данная формула является второй интерполяционной формулой Ньютона - интерполирования назад.

Формула (11) традиционно применяется для интерполирования в начале отрезка интерполяции, поэтому ее называют интерполированием вперед. Заметим, что путем переопределения узлов за начальное значение x₀ можно принимать любое табличное значение аргумента x (отбросив «лишние» узлы слева).

Когда значение аргумента находится ближе к концу отрезка интерполяции, то первую формулу становится применять невыгодно и тогда применяется формула интерполирования назад (15).

Если все узлы интерполяции являются равноотстоящими, то шаг таблицы ,

h – шаг интерполяции, то при построении интерполяционного полинома Ньютона можно использовать таблицу разностей:

x0 y0

∆y₀

x1 y1 ∆y₁²

∆y₁

X2 y2 ………………….∆y₁^N-1 (16)

……………

∆y_n-1

xn yn

∆y_kⁱ=∆y_k+1^i-1-∆y_k^i-1

Пусть для функции, заданной таблицей с постоянным шагом, составлена таблица конечных разностей (см. табл. 16). Будем ис­кать интерполяционный многочлен в виде

(17)

Это — многочлен n-й степени. Значения коэффициентов а₀, а₁, …,а_n найдем из условия совпадения значений исходной функции и многочлена в узлах.

Полагая х = х₀, из (17) находим у₀ = Р_n(x₀)= а₀, откуда а_о = у_о. Далее, полагая х = x₁, получаем

, откуда . При х = х₂ имеем

, т.е. , или , откуда

Проведя аналогичные выкладки, можно получить

Исходя из этих формул, методом полной математической ин­дукции можно доказать, что в общем случае выражение для а_к будет иметь вид

. (18)

Подставим теперь (18) в выражение для многочлена (17)

(19)

Часто эта формула записывается в другом виде. Введем вместо переменной x новую переменную t: , или, напротив, . Тогда и т.д. После этого формула (19) примет вид

(20)

При построении интерполяционного полинома Ньютона порядок расположения узлов интерполяции не играет роли, поэтому (19) перепишем:

(21)

Как и для первой формулы Ньютона, коэффициенты а₀, а₁, …,а_n находятся из условия совпадения значений функции и интер­поляционного многочлена в узлах

(22)

Подставляя (22) в (21) и переходя к переменной , получим следующий вид второй интерполяционной формулы Ньютона: (23)

Погрешность интерполяционной формулы при равноотстоящих узлах

Оценочная формула (11*) непосредственно применима для подсчета погрешности метода интерполирования по формуле Лагранжа. Используя подстановки и и заменяя соответствующим образом выражение для можно полу­чить из (11*) формулы оценки погрешностей интерполирования по первой и второй интерполяционным формулам Ньютона

(24)

(25)

Анализ интерполяционных многочленов Лагранжа и Ньютона, а также оценочных формул (11*), (24), (25) позволяет сделать по­лезные практические выводы.

Решающее влияние на значение погрешности оказывает вели­чина , которая минимизируется, когда х берется в сере­дине интервала узловых точек. При этом, когда х ближе к середи­не между двумя узловыми значениями, выгодно взять четное чис­ло п = 2т узлов (т узлов слева и т справа от х). Если же x-близко к одному из узловых значений, следует использовать нечетное чис­ло п = 2m + 1 узлов — узел, ближайший к х и по т узлов слева и справа от него.

Очевидно, что при составлении интерполяционных формул Ньютона последние слагаемые практически исчезают, если соот­ветствующие конечные разности — нули или близкие к нулю чис­ла. Поэтому в практических вычислениях интерполяционные фор­мулы Ньютона обрывают на членах, содержащих такие разности, которые в пределах заданной точности можно считать постоян­ными.

Связь между конечными разностями и точностью интерполи­рования по формулам Ньютона подтверждается следующими со­ображениями. Принимая во внимание, что при малых значениях h и при условии непрерывности можно приближенно считать , где (т.е. ) - максимальная из модулей конечных разностей (n+1)-го порядка). При этом условии оценки (24) и (25) остаточных членов первой и второй интерполяционных формул Ньютона принимают следую­щий вид:

; (26)

. (27)

Формулы (26) и (27) удобны тем, что позволяют делать оцен­ку ошибки метода интерполирования без исследования (n+1)-й производной интерполируемой функции f (в частности, когда аналитическое выражение f вовсе неизвестно).

Пример: Выполним аппроксимацию кривой намагничивания (рис.1) с помощью формулы Ньютона интерполяции назад.

Для построения интерполяционного полинома третьей степени используются значения кривой намагничивания в 4 точках:

j	0	1	2	3
Hj,А/м	0	2	15	80
Bj,Тл	0	1,1	1,45	1,5

На основании таблицы строим таблицу разделенных разностей.

0. 0

0,55

2 1,1 -0,034872

0,026923 0,000432

15. 1,45 -0,000335

0,000796

80 1,5

На основание таблицы разделенных разностей и (15) имеем:

Использование формулы Ньютона не позволяет получить удовлетворительную точность аппроксимации.

Рис.4