46. Дифференциальные уравнения 1-го порядка. Задача Коши.

Обыкновенным дифференциальным уравнением n –го порядка называется уравнение вида

F (x, y(x), y '(x), y ''(x),  …  , y⁽ⁿ⁾(x)) = 0,

где F — известная функция (n + 2)-х переменных, x — независимая переменная из интервала (a,b), y(x) — неизвестная функция. Число n называется порядком уравнения.

 

Решением дифферен­циального уравнения называется функция, которая при подстановке в уравнение обращает его в тождество

Так, решением уравнения у' = f(х) является функция у = F(x) — первообразная для функции f(x).

Рассмотрим некоторые общие сведения о дифференциальных урав­нениях (ДУ).

Если искомая (неизвестная) функция зависит oт одной перемен­ной, то ДУ называют обыкновенным; в противном случае ДУ в частных производных. Далее будем рассматривать только обыкновен­ные ДУ.

Наивысший порядок производной, входящей и ДУ, называется по-рядком этого уравнения.

Например, уравнение у'" - Зу" + 2у = 0 — обыкновенное ДУ тре­тьего порядка, а уравнение x² y’ + 5xy = у² первого порядка; yz'_x = xz'_y ДУ в частных производных первого порядка.

Процесс отыскания решения ДУ называется его интегрированием, а график решения ДУ — интегральной кривой.

Задача отыскания решения ДУ первого порядка (48-3), удовлетво­ряющего заданному начальному условию (48.4), называется задачей Коши.

y' = f(x;у)

Р(х; у) dx + Q(х; у) dy = О, 48-3

у(х_o)=у_o или у = у|_x=x0.=y₀ 48.4

I»-*.

47. Дифференциальные уравнения в полных дифференциалах.

Уравнение P(x,y)dx + Q(x,y)dy = 0 (1)

Называется уравнение полный дифференциалов если для него выполняется условие

(2)

Если выполняется условие (2) то левая часть уравнения (1) представляет собой полный дифференциал некоторой функции.

du(x,y) = 0 (3) => u(x,y) = c где c=const.

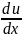dx +

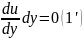
Если составить уравнение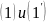 мы можем утвердить, что 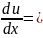P(x,y); 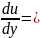Q(x,y)

u(x,y)= 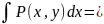u(x,y)+ϕ(y).

48. Теорема о структуре решения общего линейного однородного дифференциального уравнения с постоянными коэффициентами.

49. Определитель Вронского и его свойства.

50 Дифференциальные уравнения высших порядков, допускающие понижение порядка.

Одним из методов интегрирования ДУ высших порядков является метод понижения порядка. Суть метода состоит в том, что с помощью замены переменкой (подстановки) данное ДУ сводится к уравнению, порядок которого ниже.

Рассмотрим три типа уравнений, допускающих понижение по­рядка.

I. Пусть дано уравнение

y" = f(x) (49-6)

Порядок можно понизить, введя новую функцию р(х), положив у'= р(х). Тогда у" = p' (x) и получаем ДУ первого порядка: p' = f(х). Решив его, т. е. найдя функцию р = р(х), решим уравнение у' = р(х). Получим общее решение заданного уравнения (49.6).

II. Пусть дано уравнение

у" = f(х;у') (49.7)

не содержащее явно искомой функции у.

Обозначим у' = р, где р = p(x) — новая неизвестная функция. Тогда у" = р' и уравнение (49.7) принимает вид р‘ = f(x;p). Пусть Р = фи(x;c1) — общее решение полученного ДУ первого порядка. Заме­няя функцию р на у', получаем ДУ: у' = фи(х,c1). Оно имеет вид (49.6). Для отыскания у достаточно проинтегрировать последнее уравнение. Общее решение уравнения (49.7) будет иметь вид у = int фи(x;c1)dx+с₂.

Ш. Рассмотрим уравнение

у''= f(y; y'). (49.10)

которое не содержит явно независимой переменной х.

Для понижения порядка уравнения введем новую функцию р = = р(у), зависящую от переменной у, полагая у' = р. Дифференцируем это равенство по x, учитывая, что р – р(у(х)):

у''=d(у')/dx=dp(y)/dx=(dp(y)/dy)(dy/dx)=(dp(y)/dy)*p,

т. e. y"=p-dp/dy. Теперь уравнение (49.10) запишется в виле p*dp/dy=f(у;р).

Пусть р = фи(у;c1) является общим решением этого ДУ первого поряд­ка. Заменяя функцию р(у) на у¹, получаем у' = фи(y;c1) — ДУ с раз­деляющимися переменными. Интегрируя его, находим общий интеграл уравнения (49 10):

Int dy/(фи(y;c1))=x+c2.

51. Свойства решений линейных однородных дифференциальных уравнений с постоянными коэффициентами .

52. Построение общего решения линейного однородного дифференциального уравнения уравнений с пост. коэффициентами.

53. Теорема о структуре общего решения линейного неоднородного дифференциального уравнения.

Общее решение неоднородного уравнения y’’ + a₁y’ + a₂y = f(x) (1) представляется как всякого нибудь частного решения этого уравнения y* и общего решения y соответствующего однородного уравнения y’’ + a₁y’ + a₂y=0

54. Теорема о существовании и единственности решения задачи Коши.

Если в уравнении y' = f(x;у) функция f(х;у) и ее частная про­изводная f ’ _y (x;y) непрерывны в некоторой области D. содержащей точку (хо;уо). то существует единственное решение у = фи(x) этого уравнения, удовлетворяющее начальному условию у(х_o)=у_o или у = у|_x=x0.=y₀

55. Метод Лагранжа для нахождения частного решения линейного неоднородного дифференциального уравнения.

56. Линейные неоднородные дифференциальные уравнения с постоянными коэффициентами и специальной правой частью.

57. Системы дифференциальных уравнений. Задача Коши.

Система обыкновенных дифференциальных уравнений вида

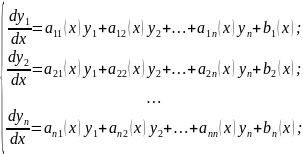
где - известные, а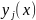 - неизвестные функции, (i = 1,2, … ,n, j = 1,2, … , n) называется линейной системой дифференциальных уравнений. При описании линейных систем дифференциальных уравнений удобнее пользоваться векторной (матричной) формой записи. Обозначим

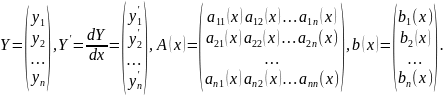
Тогда линейная система дифференциальных уравнений в векторной (матричной) форме записывается в виде Y' = A(x)Y + b(x) или, что то же самое, в виде 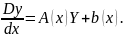Матрица A называется матрицей системы, а вектор–функция b(x) — неоднородностью системы. Система Y' = A(x)Y + b(x) называется неоднородной линейной системой дифференциальных уравнений, а система Y' = A(x)Y— однородной линейной системой. Справедлива следующая теорема существования и единственности решения задачи Коши для линейной системы дифференциальных уравнений. Если A(x) и b(x) непрерывны на отрезке [a, b] , то какова бы ни была начальная точка (x₀, Y₀) из Rn + 1, задача Коши Y' = A(x)Y + b(x), Y(x₀) = Y₀, имеет единственное на [a,b] решение Y = Y(x) .