
- •1.3. Твердые растворы
- •1.Экстремумы функций. Возрастание и убывание функций.
- •2.Выпуклость, точки перегиба, асимптоты графика функций.
- •3.Первообразная функции и неопределенный интеграл. Таблица неопределенных интегралов.
- •4.Замена переменной в неопределенном интеграле. Метод интегрирования по частям.
- •8.Замена переменной в определенном интеграле. Формула интегрирования по частям для определенного интеграла.
- •5.Определенный интеграл и его геометрический смысл.
- •6.Основные свойства определенного интеграла.
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •14.Производные и дифференциалы высших порядков для функций многих переменных. Формула Тейлора
- •16.Площадь фигуры и объём тела
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
- •1.3. Твердые растворы
1.3. Твердые растворы
Твердые растворы (ТР) - кристаллические фазы переменного состава, в которых атомы элемента В размещаются в пространственной решетке элемента А, не изменяя ее типа.
Для ТР характерен металлический тип межатомной связи. Твердые растворы обозначают: , , , или А(В). Твердые растворы всегда более тверды, чем чистые металлы, менее пластичны. Их образование всегда сопровождается увеличением электрического сопротивления, как правило, снижаются пластичность и вязкость. Твердые растворы бывают упорядоченными и неупорядоченными. Твердые растворы, устойчивые при сравнительно низких температурах, получили название упорядоченных твердых растворов, или сверхструктур. Полностью упорядоченные растворы образуются в том случае, когда отношение компонентов в сплаве равно целому числу: 1:1, 1:2, 1:3 и т.д. Они занимают промежуточное положение между твердыми растворами и химическими соединениями. При изменении температуры происходит разупорядочение ТР с соответствующим изменением свойств. Температуру разупорядочения к называют точкой Курнакова. Упорядоченные твердые растворы обозначают буквами ’, ’, ’, ’. Все металлы могут в той или иной степени взаимно растворяться друг в друге в твердом состоянии. В тех случаях, когда компоненты могут замещать друг друга в кристаллических решетках в любых количественных соотношениях, образуется непрерывный ряд твердых растворов. Твердые растворы замещения с неограниченной растворимостью могут образоваться при соблюдении следующих условий: 1. Компоненты должны обладать одинаковыми по типу (изоморфными) кристаллическими решетками. 2. Различие в атомных размерах компонентов должно быть не значительным и не превышать 8 – 15 %. 3. Компоненты должны принадлежать к одной и той же группе периодической системы элементов или к смежным родственным группам и в связи с этим иметь близкое строение валентной оболочки электронов в атомах.
где - вектор Лангранжа.
-Составим систему из уравнений
-Если полученная система имеет решение, то есть решение исходной задачи
3. произведение интегрируемых ф-ций.
2)z1* z2= r1r2(cos φ1+ isin φ1 )( cos φ2 + i sin φ2)= r1r2(cos φ1 cos φ2 +i cos φ1 sin φ2+ isin r1r2cos φ2 -sin φ1 sin φ2)= r1r2(cos(φ1+φ2)+isin(φ1+φ2)
|
Из этой формулы след. формула Муавра: 3)
|
4. +isin ,k=0,n-1
4.Ф-ции P и Q удовлетв. условию Эйлера
Замечание.При нахождении ф-ции F за основу можно брать рав-во ,котор. сначало интегрир. по перемен. y,а затем дифференц. по перем. x.
1.3. Твердые растворы
Твердые растворы (ТР) - кристаллические фазы переменного состава, в которых атомы элемента В размещаются в пространственной решетке элемента А, не изменяя ее типа.
Для ТР характерен металлический тип межатомной связи. Твердые растворы обозначают: , , , или А(В). Твердые растворы всегда более тверды, чем чистые металлы, менее пластичны. Их образование всегда сопровождается увеличением электрического сопротивления, как правило, снижаются пластичность и вязкость. Твердые растворы бывают упорядоченными и неупорядоченными. Твердые растворы, устойчивые при сравнительно низких температурах, получили название упорядоченных твердых растворов, или сверхструктур. Полностью упорядоченные растворы образуются в том случае, когда отношение компонентов в сплаве равно целому числу: 1:1, 1:2, 1:3 и т.д. Они занимают промежуточное положение между твердыми растворами и химическими соединениями. При изменении температуры происходит разупорядочение ТР с соответствующим изменением свойств. Температуру разупорядочения к называют точкой Курнакова. Упорядоченные твердые растворы обозначают буквами ’, ’, ’, ’. Все металлы могут в той или иной степени взаимно растворяться друг в друге в твердом состоянии. В тех случаях, когда компоненты могут замещать друг друга в кристаллических решетках в любых количественных соотношениях, образуется непрерывный ряд твердых растворов. Твердые растворы замещения с неограниченной растворимостью могут образоваться при соблюдении следующих условий: 1. Компоненты должны обладать одинаковыми по типу (изоморфными) кристаллическими решетками. 2. Различие в атомных размерах компонентов должно быть не значительным и не превышать 8 – 15 %. 3. Компоненты должны принадлежать к одной и той же группе периодической системы элементов или к смежным родственным группам и в связи с этим иметь близкое строение валентной оболочки электронов в атомах.
25.Линейное
пространство: определение и примеры.
Определение1.Мн-во
V
с определ-ми на нем операц. сложен. вект.
и умнож. вект. на число
назыв.веществ.вектор.(линейн) простр-ом,если
указанные операц. облад след св-ами:
1.x+y=y+x(коммуникативность)
2.x+(y+z)=(x+y)+z(ассоциативность)
3.сущ. нулевой
элем. мн-ва V,обознач.
0,такой что 0+x=x,
0,х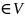 4.для
4.для
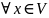 сущ.
противопол элем -х
,такой
что х+-х=0
5.
сущ.
противопол элем -х
,такой
что х+-х=0
5.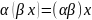 ,
,
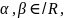 x
6.
x
6.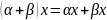 ,
x
7.
,
x
7.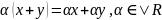 ,
x,y
8.1*x=x
x
,
x,y
8.1*x=x
x
Примеры:
1.Если V
есть мн-во своб вект.|R3
c
обычным пониманием опер слож вект. и
умнож.вект. на число.
2.мн-во
 -мн-во
матриц размера m
-мн-во
матриц размера m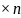 ,
в кот. сложение вект и умнож вект на
число понимаются всмысле сложен матриц
и умножение матрицы на число.
3.мн-во
,
в кот. сложение вект и умнож вект на
число понимаются всмысле сложен матриц
и умножение матрицы на число.
3.мн-во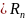 [x]-мн-во
многочленов с действит коэффиц степени
[x]-мн-во
многочленов с действит коэффиц степени
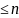 .Операции
слож вект и умнож вектора на число
поним. в обычном смысле слож многочлена
и умнож многочленов на число.
Замечание. комплексное
вект. Пространство опред. так же,как и
веществ. вект. пр=во,если только в опред.1
мн-во
.Операции
слож вект и умнож вектора на число
поним. в обычном смысле слож многочлена
и умнож многочленов на число.
Замечание. комплексное
вект. Пространство опред. так же,как и
веществ. вект. пр=во,если только в опред.1
мн-во
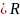 заменить на мн-во C.
заменить на мн-во C.
26.Линейная
зависимость и независимость векторов
в линейном пространстве.
Определение1.Сис-ма
векторов a1…an(или
векторы)назыв. линейно-независ.,если
их лин. комбин. а=0 только в том случае,
если все
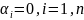 , в противном случаи данная сист. век-ов
(векторы)назыв. лин-зависимыми.
Другими
словами векторы a1…an
лин-зависимы,если
сущ. числа
, в противном случаи данная сист. век-ов
(векторы)назыв. лин-зависимыми.
Другими
словами векторы a1…an
лин-зависимы,если
сущ. числа
 ,
,
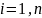 одновремнно не равные нулю такие,что
линейн комбин.
одновремнно не равные нулю такие,что
линейн комбин.
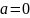 Утверждение
1.Если в сик.
вект-ов a1…an
имеется
нулевой вектор,то система векторов
лин-зависимы.
Док-во.Пусть
а1=0.Составим
a=
Утверждение
1.Если в сик.
вект-ов a1…an
имеется
нулевой вектор,то система векторов
лин-зависимы.
Док-во.Пусть
а1=0.Составим
a=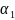 a1+
a1+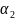 a2+….+
a2+….+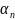 an,где
-любое
число,
an,где
-любое
число,
 …
=0,a=0.
Утверждение2.Если
некот. из век-ов в сист. a1…an
явл.
лин-зависимыми,то и вся система вект.
лин-зависима.
Утверждение
3.Векторы
a1…an
лин-зависимы
тогда,когда хотя бы один из них выражается
через остальные.
Док-во.Пусть
для определ-сти вект а1
выражается через остальные,т.е.а1=
a2+…
…
=0,a=0.
Утверждение2.Если
некот. из век-ов в сист. a1…an
явл.
лин-зависимыми,то и вся система вект.
лин-зависима.
Утверждение
3.Векторы
a1…an
лин-зависимы
тогда,когда хотя бы один из них выражается
через остальные.
Док-во.Пусть
для определ-сти вект а1
выражается через остальные,т.е.а1=
a2+…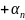 an.
Положим
an.
Положим
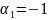 ,тогда
лин. комбин.
a1+
a2+….+
an=0(1),т.е.
вект лин-зависимы.
Пусть
теперь векторы a1…an
лин-зависимы,тогда
имеет место (2) причем (2)не все
,тогда
лин. комбин.
a1+
a2+….+
an=0(1),т.е.
вект лин-зависимы.
Пусть
теперь векторы a1…an
лин-зависимы,тогда
имеет место (2) причем (2)не все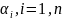 равны 0.предположим для определ.,что
равны 0.предположим для определ.,что
 ,тогда
из (2)
,тогда
из (2)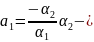 …-
…-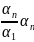 ,
т.е.
вектор а1
выражается через остальные векторы
сис-мы
,
т.е.
вектор а1
выражается через остальные векторы
сис-мы
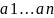 .
.
27.Базис и
размерность линейных пространств.
Координаты вектора. Рассм.
вект. пр-во V.
Определение.Сис-ма
вект. векторного пр-ва V
назыв базисом,если она лин-независ. и
каждый вектор пр-ва V
выраж. через неё.Лин. пр-во V,имеющее
базис,сотоящий из конечного числа
элементов назыв конечномерным.Число
элементов входящих в базис назыв
размерностью пр-ва V.
Пусть в
пр-ве V
задан базис (e1…en),т.е.
пр-во V
явл конечномерным.Его размерность
будем обозначать dim,т.е.dimV=n,далее
будем обозн. Vn.
Утверждение1.В
пр-ве Vn
любая линейно-независ сис-ма nвекторов
явл. базисом.
x
=
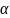 1e1
+ … +
nen. (1) Выражение
(1) называется разложением
вектора x
по базису
e1,
… , en
. Если обозначим базис E=(e1…en),ввести
вектор
1e1
+ … +
nen. (1) Выражение
(1) называется разложением
вектора x
по базису
e1,
… , en
. Если обозначим базис E=(e1…en),ввести
вектор
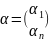 (координаты
столбец вектора х),то рав-во (1) можно
записать в виде x=E
.
Замечание.Обратим
внимание,что базисные векторы
упорядоченные.Если измен. порядок
следования векторов в базисе,то получим
новый базис.
Теорема1.Координаты
вектора в заданном базисе определ
одназначно.Другое разложение вектора
по базису единственное.
Теорема2.Два
век-ра в пр-ве Vn
равны тогда,когда равны их соответствуюшие
координаты.
(координаты
столбец вектора х),то рав-во (1) можно
записать в виде x=E
.
Замечание.Обратим
внимание,что базисные векторы
упорядоченные.Если измен. порядок
следования векторов в базисе,то получим
новый базис.
Теорема1.Координаты
вектора в заданном базисе определ
одназначно.Другое разложение вектора
по базису единственное.
Теорема2.Два
век-ра в пр-ве Vn
равны тогда,когда равны их соответствуюшие
координаты.
28.Преобразование
координат. Пусть
в Vn
задано 2 вектора(базиса) F= )и
F′=(
)и
F′=(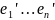 )и
пусть вектор Х
)и
пусть вектор Х![]() Vn
в базисе Е имеет координаты α=
Vn
в базисе Е имеет координаты α=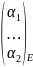 (т.е. вектор-столбец координат), и в
базисе имеет координаты α′=
(т.е. вектор-столбец координат), и в
базисе имеет координаты α′= Здесь индексы
Здесь индексы
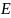 и
и
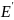 указывают на базисы, взятые в соответствии
с координатами. Установим связь между
α и α′.
Сначала
элементы в
разложим по базису Е:
указывают на базисы, взятые в соответствии
с координатами. Установим связь между
α и α′.
Сначала
элементы в
разложим по базису Е:
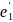 =
=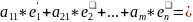 )(
)(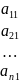 )
……………………………………………………………….
(1)
)
……………………………………………………………….
(1)
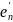 =
=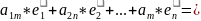 )(
)(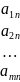 )
Если ввести матрицу А=
)
Если ввести матрицу А=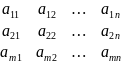 ,то (1) можно заменить Е′=ЕА (2) Матрица
А называется матрицей перехода от
базиса Е к Е′. Обратим внимание, что
каждый k-ый
столбец матрицы А представляет собой
координаты вектора
,то (1) можно заменить Е′=ЕА (2) Матрица
А называется матрицей перехода от
базиса Е к Е′. Обратим внимание, что
каждый k-ый
столбец матрицы А представляет собой
координаты вектора
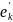 в базисе Е. А поскольку базисные вектора
линейно независимые, то и столбцы А
линейно независимы, т.е. матрица А
невырожденная.
в базисе Е. А поскольку базисные вектора
линейно независимые, то и столбцы А
линейно независимы, т.е. матрица А
невырожденная.
Построим вектор Х ,с использ. координат его можно записать: Х=Еα-Е′α′
Это равенство в силу А перепишем в виде Еα=ЕАα′=>Е(α-Аα)′, отсюда α=Аα′(3) Формула (3) выражает зависимость между координатами вектора Х в базисе Е и Е′, т.е. зная координаты базиса Е в Е′ по формуле(3) можно найти координаты вектора, верно и обратное, т.к. из (3) следует:
Α=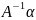
.
31.Преобразование
матрицы линейного оператора при переходе
к новому базису. Подобные матрицы
Пусть V –
линейное пространство, заданное
двумя базисами е=
)
и е′=(
).
Пусть S матрица
перехода от базиса к базису e’,
т.е. Е′=SE
(1)
Пусть
f
– линейный оператор, действующий в
пр-ве Vn,
матрица которого в базисе Е обозначена
через А, а в базисе Е′ через В. Возьмем
х
Vn
и положим у=f(x).
Векторы х и у разложим по базисам Е
и Е′: x=EX=E′X′
y=EY=E′Y′
(2)
Используемые
матрицы А и В запишем :У=АХ, У′=ВХ′,
SY=BSX
, SAX=BSX
– это равенство справедливо для любого
вектора х, поэтому S′A=BS,
A=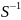 BJ(или
B=SA
)(3).
(3) устанавливает связь между матрицами
1-ого и также лин. оператора в разных
базисах. Определение: матрицы А и В
называются подобными, если существует
невырожденная матрица S
, что A=
BS,
В=
AS
При этом матрица S
называется трансформирующей. Ра-ва A=
BJ
называется преобразованием подобия
или преобразованием матрицы. Свойства:
1)Если А~В,
В~С, то А~С, А=
BS,
B=
BJ(или
B=SA
)(3).
(3) устанавливает связь между матрицами
1-ого и также лин. оператора в разных
базисах. Определение: матрицы А и В
называются подобными, если существует
невырожденная матрица S
, что A=
BS,
В=
AS
При этом матрица S
называется трансформирующей. Ра-ва A=
BJ
называется преобразованием подобия
или преобразованием матрицы. Свойства:
1)Если А~В,
В~С, то А~С, А=
BS,
B=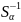 С
С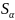 => A=
=> A=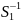 C
C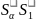 =
=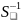 C
C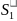 S=
S=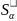 S
2)определители
и ранги подобных матриц равны
S
2)определители
и ранги подобных матриц равны
32.Собственные
векторы и собственные значения линейного
оператора Определение:
Если для некоторого Х
Vn,
x
не равен 0 существует λ такое, что f(x)
= λx,
то вектор х называется собственным, а
число λ собственным значением оператора
f,
соответствующее собственному вектору
х. Множество всех собственных значений
f
называется спектром оператора f.
Если
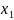 =
= =>
=>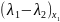 =0
=> т.к. х не равен 0=>
=0
=> т.к. х не равен 0=>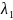 =
=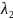 Замечание:
Одному и тому же собственному значению
может соответствовать множество
собственных векторов, линейно зависимых
между собой. Определение:
Пусть А – произвольная матрица, λ –
некоторое число, J
– единичная матрица. Матрица А-λJ
называется хар-ой матрицей по отношению
к А. Определитель этой матрицы det(A-λJ)
называется хар-м многочленом матрицы
А
Замечание:
Одному и тому же собственному значению
может соответствовать множество
собственных векторов, линейно зависимых
между собой. Определение:
Пусть А – произвольная матрица, λ –
некоторое число, J
– единичная матрица. Матрица А-λJ
называется хар-ой матрицей по отношению
к А. Определитель этой матрицы det(A-λJ)
называется хар-м многочленом матрицы
А
![]() Тогда det(A-λJ)=
Тогда det(A-λJ)=
![]() =φ(λ)
Если раскрыть этот определитель, то
можно увидеть, что φ(λ) будет представлять
собой многочлен степени n
– ровно столько корней он имеет.
Замечание: многочлен степени n
может иметь действ. Корней меньше, чем
n.
Итак, для нахождения собственных
значений и собственных векторов решение
уравнения
=φ(λ)
Если раскрыть этот определитель, то
можно увидеть, что φ(λ) будет представлять
собой многочлен степени n
– ровно столько корней он имеет.
Замечание: многочлен степени n
может иметь действ. Корней меньше, чем
n.
Итак, для нахождения собственных
значений и собственных векторов решение
уравнения
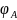 (λ)=0.
Пусть
(λ)=0.
Пусть
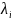 – корни этого уравнения. Если пространство
Vn
является вещественным линейным
пространством, то из найденных чисел
– корни этого уравнения. Если пространство
Vn
является вещественным линейным
пространством, то из найденных чисел
ост. Только действительные числа. В случае камп-ого линейного пространства берем все
Числа
являются собственными значениями
оператораf(A).
Для каждого собственного значения
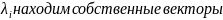 ,
ему соответствующие. Для этого решаем
СЛАУ: (А-
J)X=0
(1)
,
ему соответствующие. Для этого решаем
СЛАУ: (А-
J)X=0
(1)
В общем случае она может иметь бесконечно много решений
Замечание:
Пусть имеем многочлен P(λ).
Под кратностью к корня
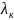 уравнения P(λ)=0
понимают кол-во раз сколько он встречается
в наборе тех корней многочлена P(λ).
уравнения P(λ)=0
понимают кол-во раз сколько он встречается
в наборе тех корней многочлена P(λ).
Если
корень мн-ва P(λ)
кратности к, то P(λ)=0
Р(к)=0
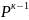 (λк)=0
(λк)=0
Кроме
того P(λ)
пред. В виде P(λ)=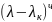 φλ,
где φλ – многочлен степени degP(
φλ,
где φλ – многочлен степени degP(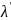 -λ)
-λ)
33.Приведение
матрицы линейного оператора к
диагональному виду Теорема
1.
Линейный оператор A в Rn приводится
к диагональному виду тогда и только
тогда, тогда его собственные векторы
образуют базис в Rn.
Доказательство.
Необходимость(. Пусть в базисе ![]() матрица
оператора A диагональная:
матрица
оператора A диагональная:
А=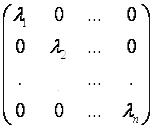
Тогда ![]() ,
, ![]() ,….,
,…., ![]() ,
т.е. базис
,
т.е. базис ![]() состоит
из собственных векторов, отвечающих
собственным значениям
состоит
из собственных векторов, отвечающих
собственным значениям ![]() .
Достаточность . Пусть
.
Достаточность . Пусть ![]() базис
из собственных векторов, отвечающих
собственным значениям
.
Тогда
,….,
базис
из собственных векторов, отвечающих
собственным значениям
.
Тогда
,….,![]() ,
и
,
и
А=
Укажем достаточное условие приводимости оператора к диагональному виду.
Теорема
2.
Если линейный оператор ![]() в
в ![]() имеет
имеет ![]() различных
собственных значений, то собственные
векторы, отвечающие им, образуют базис
в
,
а матрица оператора в этом базисе
диагональная.
различных
собственных значений, то собственные
векторы, отвечающие им, образуют базис
в
,
а матрица оператора в этом базисе
диагональная.
Доказательство
для ![]() . Пусть
. Пусть ![]() -
собственные значения, а
-
собственные значения, а ![]() -собственные
векторы оператора
в
-собственные
векторы оператора
в ![]() .
Покажем, что эти векторы линейны
независимы. Пусть
.
Покажем, что эти векторы линейны
независимы. Пусть ![]()
![]() и
и ![]()
Отсюда
![]()
![]()
Значит, ![]() .
Аналогично,
.
Аналогично, ![]() .
Теорема доказана.
.
Теорема доказана.
29.Линейные
отображения. Линейные операторы Пусть
v
и
 векторные пространства, отображение
f:
v→
называется линейным, если:
1)
векторные пространства, отображение
f:
v→
называется линейным, если:
1)![]() ,
,
![]() для всех х,
у
Vи α
R.
Таким образом линейные преобразования
сохраняют линейные операции. Обратим
внимание, что в соответствии (х+у), α(х)
используются операции сложения и
умножения определены в пространстве
V,
а f(x)
+ f(x),
αf(x)
определены в пространстве V′.
V
и V′
в общем случае могут отличаться
Свойства линейных преобразований:
1)Если f
:v→
линейное преобразование, и векторы(
…
для всех х,
у
Vи α
R.
Таким образом линейные преобразования
сохраняют линейные операции. Обратим
внимание, что в соответствии (х+у), α(х)
используются операции сложения и
умножения определены в пространстве
V,
а f(x)
+ f(x),
αf(x)
определены в пространстве V′.
V
и V′
в общем случае могут отличаться
Свойства линейных преобразований:
1)Если f
:v→
линейное преобразование, и векторы(
…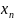 )
линейно зависимы в пространстве V
, то линейно зависимы вектора f(
),
f(
)
линейно зависимы в пространстве V
, то линейно зависимы вектора f(
),
f(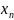 )
Примеры: преобразование i:
V→V′,
i(x)
1)f(x)=Ax
, где Ax
– матрица размера m*n
2)Преобразование
f:R→
и действия по правилу F(x)=f(
)
Примеры: преобразование i:
V→V′,
i(x)
1)f(x)=Ax
, где Ax
– матрица размера m*n
2)Преобразование
f:R→
и действия по правилу F(x)=f(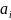 +
+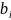 )=
)=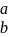 a+ib
не принадлежит С
Примеры
лин.оператора:
1)В прос-ве
a+ib
не принадлежит С
Примеры
лин.оператора:
1)В прос-ве
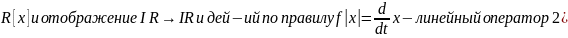 2)Умножение
матрицы-столбца(строки) на квадратную
матрицу 3)В пространстве свобод.векторов
поворот вектора на заданный угол
2)Умножение
матрицы-столбца(строки) на квадратную
матрицу 3)В пространстве свобод.векторов
поворот вектора на заданный угол
30.Матрица линейного
оператора Пусть
Vn
векторные пространства, f
– лин. Оператор,Е=
)
– базис в Vn.
Раз f:Vn
в себя, то элементы f(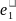 )
, f(
)
, f(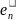 )
будут элементами пр-ва Vn
, а значит их можно разложить по базису
Е
)
будут элементами пр-ва Vn
, а значит их можно разложить по базису
Е
f(
)=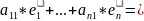 )
)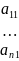
………………………………………………….. (1)
g(
)=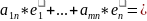 )
)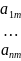 Составим
матрицу А=
Составим
матрицу А=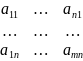 Обозначим f(E)=f(
Обозначим f(E)=f(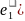 …f(
…f(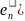 Тогда (1) можно записать в виде:f(E)=EA.
Матрица А называется матрицей линейного
оператора f
в базисе Е. Заметим, что матрица А зависит
от базиса. Итак, показали, что каждому
лин. оператору соответствует в заданном
базисе матрица, верно и обратное. Обратим
внимание, что каждый k-ый
столбец матрицы А представляет собой
координаты элемента f(
Тогда (1) можно записать в виде:f(E)=EA.
Матрица А называется матрицей линейного
оператора f
в базисе Е. Заметим, что матрица А зависит
от базиса. Итак, показали, что каждому
лин. оператору соответствует в заданном
базисе матрица, верно и обратное. Обратим
внимание, что каждый k-ый
столбец матрицы А представляет собой
координаты элемента f(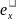 ).
Возьмем Х
Vn
и положим у=f(х).
Пусть Х, У координаты столбца-вектора
х и у в базисе Е, тогда ЕУ=f(x)=f(EX)=f(E)X=EAX
Из этого равенства на основании того,
что базисные векторы линейно независимы,
).
Возьмем Х
Vn
и положим у=f(х).
Пусть Х, У координаты столбца-вектора
х и у в базисе Е, тогда ЕУ=f(x)=f(EX)=f(E)X=EAX
Из этого равенства на основании того,
что базисные векторы линейно независимы,
оординатный столбец, т.е. любой лин. оператор можно определить соотношением (2)
34.Евклидово пространство. Ортогональный и ортонормированный базисы ЕВКЛИДОВО ПРОСТРАНСТВО - конечномерное векторное пространство с положительно определённым скалярным произведением. Является непосредств. обобщением обычного трёхмерного пространства. В Е. п. существуют декартовы координаты, в к-рых скалярное произведение (ху)векторов х- (x1, . . . , хn)и y = (y1, . . . , yп)имеет вид (xy)=x1y1+. . .+хnуп. В произвольных координатах скалярное произведение по определению удовлетворяет условиям: 1) (хх)/0, (хх) = 0 лишь при x=0; 2) (ху) = (ух)*; 3) (aху) = a(ху); 4) (x{y+z}) =(xy)+ (xz), где a - любое комплексное число, * означает комплексное сопряжение. Базис e1, e2, … , en в n –мерном евклидовом пространстве En называется ортогональным, если (ei, ej) = 0 i ≠ j , т.е. все векторы попарно ортогональны. Ортогональный базис из единичных векторов называется ортонормированным. Теорема. В любом евклидовом пространстве существует ортонормированный базис. Доказательство (метод ортогонализации Грама–Шмидта). Пусть f1, f2, … , fn — произвольный базис в En . Построим ортогональный базис e1, e2, … , en следующим образом. Положим e1 = f1 , e2 = f2 + αe1 . Найдем α из условия ортогональности: (e1, e2) = 0 (f2, e1) + α (e1, e1) = 0.
|
Отсюда
|
|
|
Предположим теперь, что уже построена ортогональная система из k − 1 ненулевого вектора — e1, e2, … , ek − 1 . Тогда вектор ek ищем в виде
|
|
(1) |
Из условий ортогональности вектора ek и векторов e1, e2, … , ek − 1
|
|
|
|
|
|
|
|
|
|
|
|
получаем
|
|
|
|
|
|
|
|
|
|
|
|
Отсюда
|
|
35.Квадратичная
форма —
функция на векторном пространстве,
задаваемая однородным
многочленом второй
степени от координат вектора.
Пусть L есть векторное
пространство над полем K и ![]() —
базис в L.
Функция
—
базис в L.
Функция ![]() называется
квадратичной формой, если её можно
представить в виде
называется
квадратичной формой, если её можно
представить в виде![]() где
где ![]() ,
а
,
а ![]() —
некоторые элементы поля K.
Свойства:---Квадратичная
форма является положительно определенной,
тогда и только тогда, когда все
угловые миноры её
матрицы строго положительны.---Квадратичная
форма является положительно определенной,
тогда и только тогда, когда все
угловые миноры её
матрицы строго положительны.---Для
приведения квадратичной формы к
каноническому виду обычно используется метод
Лагранжа
Из коэффициентов квадратичной
формы составим симметричную матрицу
А=
—
некоторые элементы поля K.
Свойства:---Квадратичная
форма является положительно определенной,
тогда и только тогда, когда все
угловые миноры её
матрицы строго положительны.---Квадратичная
форма является положительно определенной,
тогда и только тогда, когда все
угловые миноры её
матрицы строго положительны.---Для
приведения квадратичной формы к
каноническому виду обычно используется метод
Лагранжа
Из коэффициентов квадратичной
формы составим симметричную матрицу
А=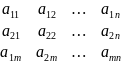
которую назовем матрицей квадратичной формы.
36.Метод Лагранжа — метод приведения квадратичной формы к каноническому виду
Метод
Лагранжа - это просто метод выделения
полных квадратов. Например:
![]() (собираем
все слагаемые с
(собираем
все слагаемые с ![]() )
)
![]() (обозначаем
(обозначаем ![]() )
)
![]() .
Если
на каком-то шаге нет квадрата очередной
переменной, но есть смешанное произведение,
то надо сделать замену типа
.
Если
на каком-то шаге нет квадрата очередной
переменной, но есть смешанное произведение,
то надо сделать замену типа ![]() ,
, ![]() ,
чтобы квадрат появился.
,
чтобы квадрат появился.
