
- •Часть 2
- •Нижний Новгород 2005
- •Содержание
- •Электростатика
- •1.1. Электрическое поле в вакууме Основные определения
- •1.2. Электрическое поле в диэлектриках Основные определения
- •1.3. Проводники. Конденсаторы. Энергия электрического поля Основные определения
- •1.4. Примеры решения задач
- •Постоянный ток
- •2.1. Плотность тока. Подвижность носителей заряда Основные определения
- •2.2. Электродвижущая сила. Правила Кирхгофа
- •2.3. Работа и мощность в цепях постоянного тока
- •2.4. Примеры решения задач
- •Магнитостатика
- •3.1. Магнитное поле в вакууме Основные определения
- •3.2. Сила Лоренца. Сила Ампера1 Основные определения
- •3.3. Магнитное поле в веществе Основные определения
1.4. Примеры решения задач
З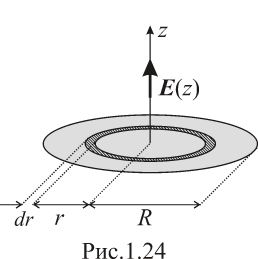 адача
1.4
адача
1.4
Для
того чтобы вычислить потенциал и
напряженность поля, создаваемого данной
системой зарядов, необходимо использовать
принцип суперпозиции (формула 1.1г).
Разобьем круглую однородно заряженную
пластину радиусом
на множество тонких концентрических
колец толщиной
![]() каждое (рис.1.24). В соответствии с решением
задачи 1.3
потенциал электрического поля в
произвольной точке на оси
,
создаваемый любым из этих колец, в том
числе, выделенным на рисунке темной
штриховкой, равен
каждое (рис.1.24). В соответствии с решением
задачи 1.3
потенциал электрического поля в
произвольной точке на оси
,
создаваемый любым из этих колец, в том
числе, выделенным на рисунке темной
штриховкой, равен
![]() .
Потенциал, создаваемый всей пластиной,
можно вычислить путем интегрирования:
.
Потенциал, создаваемый всей пластиной,
можно вычислить путем интегрирования:
![]() . (*)
. (*)
Исходя
из соображений симметрии, можно
утверждать, что напряженность
электрического поля, создаваемая каждым
из колец в отдельности
![]() и всей пластиной в целом, направлена
вдоль оси
:
и всей пластиной в целом, направлена
вдоль оси
:
![]() .
С другой стороны, как следует из
соотношения (1.1д),
.
С другой стороны, как следует из
соотношения (1.1д),
![]() .
Таким образом,
.
Таким образом,
![]()
![]() . (**)
. (**)
Исследуем
полученные результаты. В предельном
случае больших расстояний
![]() выражения (*) и (**) принимают вид
выражения (*) и (**) принимают вид
![]() и
и
![]() ,
что совпадает с выражениями для поля
точечного заряда
,
что совпадает с выражениями для поля
точечного заряда
![]() .
Именно таким зарядом представляется
пластина с точки зрения наблюдателя,
находящегося на большом удалении от
нее.
.
Именно таким зарядом представляется
пластина с точки зрения наблюдателя,
находящегося на большом удалении от
нее.
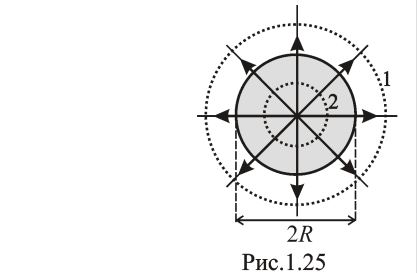 В
другом предельном случае
В
другом предельном случае![]() из (*) и (**) получаются выражения для поля,
создаваемого пластиной неограниченных
размеров:
из (*) и (**) получаются выражения для поля,
создаваемого пластиной неограниченных
размеров:
![]() ,
,
![]() .
.
Задача 1.24
Заряды распределены сферически симметрично относительно начала координат. Такой же симметрией характеризуется и картина силовых линий напряженности электрического поля (рис.1.25). Это позволяет использовать для решения задачи теорему Остроградского-Гаусса (формула 1.1к).
Найдем напряженность поля вне заряженного шара. Для этого в качестве гауссовой поверхности выберем сферу радиусом , принимающим произвольное значение в интервале
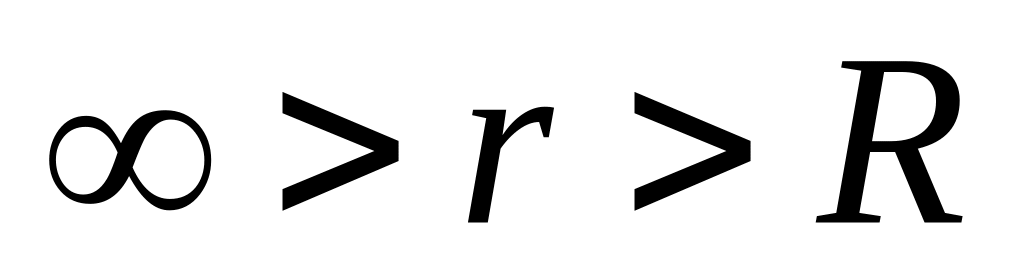 (сфера 1 на рис. 1.25). Поток вектора
напряженности электрического поля
через любой элементарный участок
этой поверхности
(сфера 1 на рис. 1.25). Поток вектора
напряженности электрического поля
через любой элементарный участок
этой поверхности
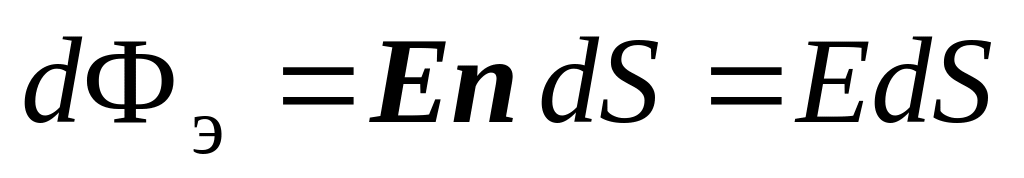 ,
поскольку вектор
и единичный вектор
внешней нормали к поверхности всегда
в силу вышеупомянутой симметрии
параллельны друг другу. Поток через
поверхность указанной сферы
,
поскольку вектор
и единичный вектор
внешней нормали к поверхности всегда
в силу вышеупомянутой симметрии
параллельны друг другу. Поток через
поверхность указанной сферы
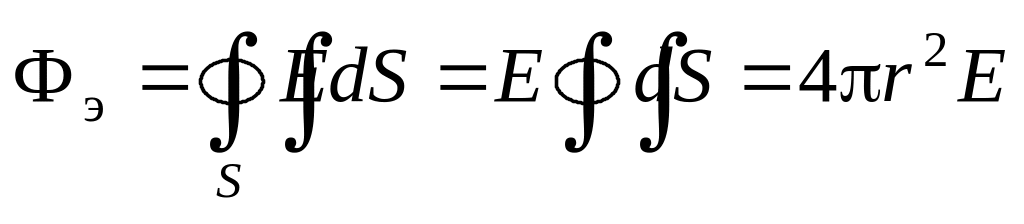 .
(Здесь использовано то обстоятельство,
что в силу той же симметрии величина
постоянна во всех точках сферы, и на
этом основании ее можно вынести за
знак интеграла). С другой стороны, в
соответствии с (1.1к),
.
(Здесь использовано то обстоятельство,
что в силу той же симметрии величина
постоянна во всех точках сферы, и на
этом основании ее можно вынести за
знак интеграла). С другой стороны, в
соответствии с (1.1к),
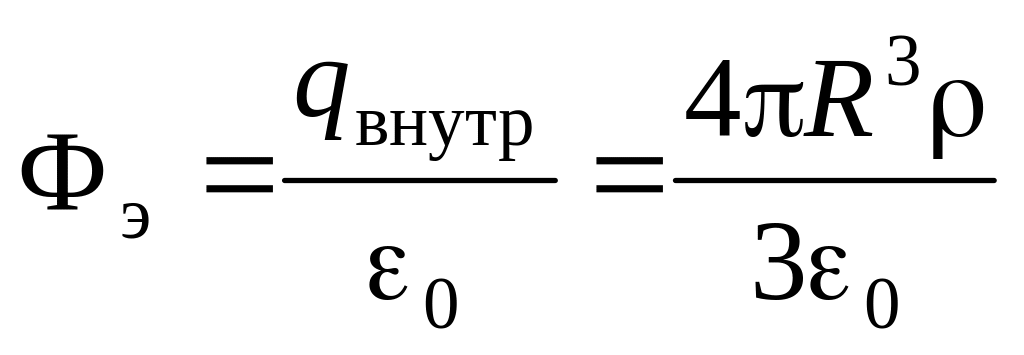 .
Объединяя эти выражения, получим
.
Объединяя эти выражения, получим
![]() при
. (*)
при
. (*)
Процедура определения зависимости внутри шара отличается тем, что поток вектора через поверхность сферы 2 радиусом
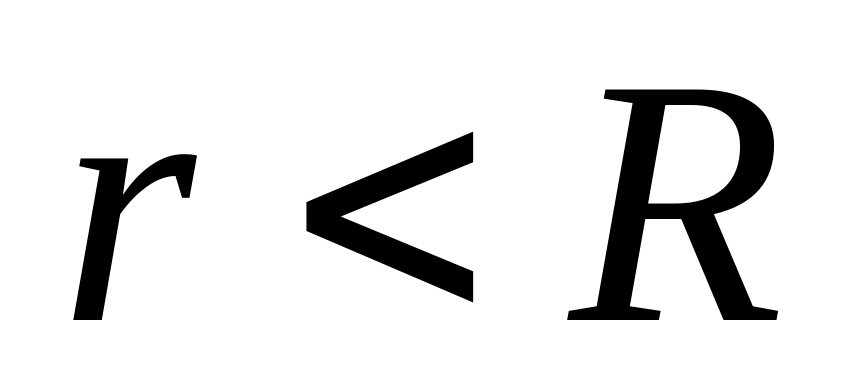 определяется не всем зарядом шара, а
только той его частью, которая находится
внутри этой сферы:
определяется не всем зарядом шара, а
только той его частью, которая находится
внутри этой сферы:
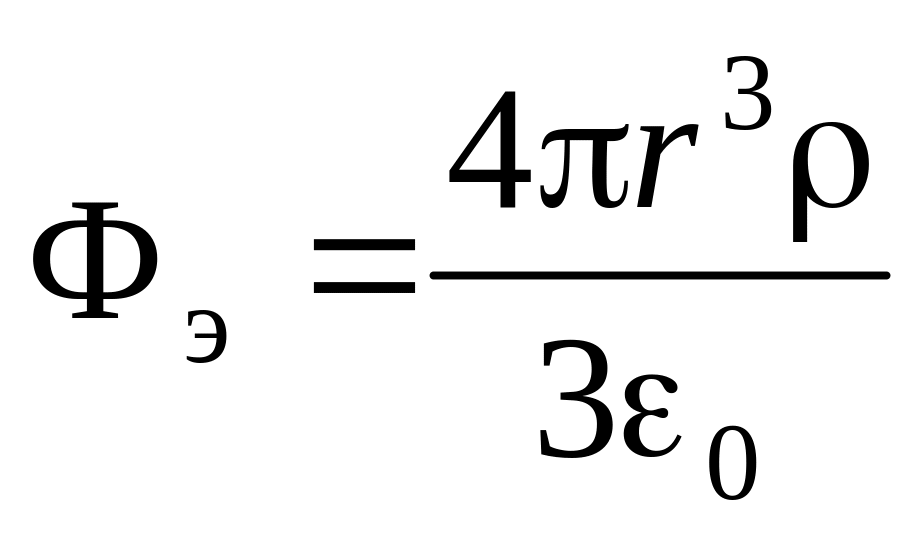 .
Таким образом,
.
Таким образом,
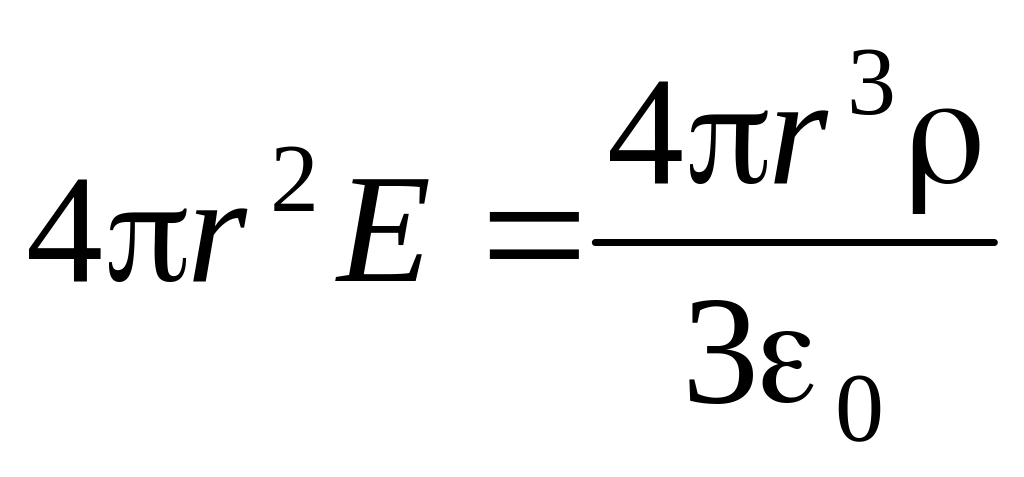 ,
откуда следует, что
,
откуда следует, что
![]() при
. (**)
при
. (**)
Зависимость потенциала электрического поля от , как следует из второй формулы в (1.1д), в обеих рассматриваемых частях пространства имеет вид
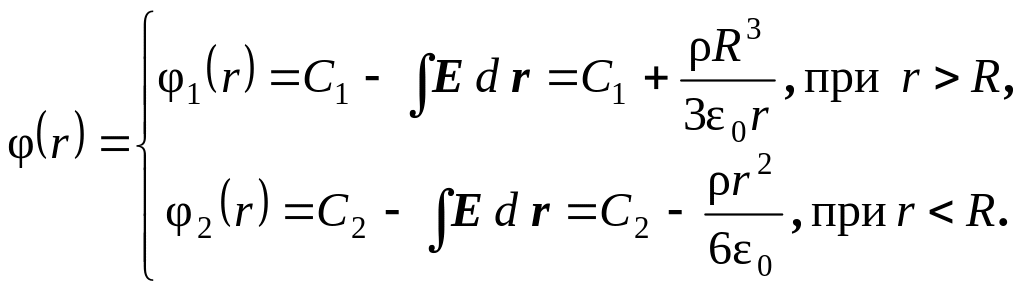 Константы
Константы
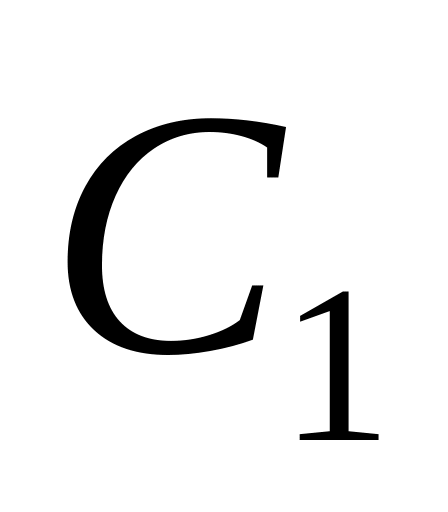 и
определяются однозначно, если
потребовать, чтобы функция
и
определяются однозначно, если
потребовать, чтобы функция
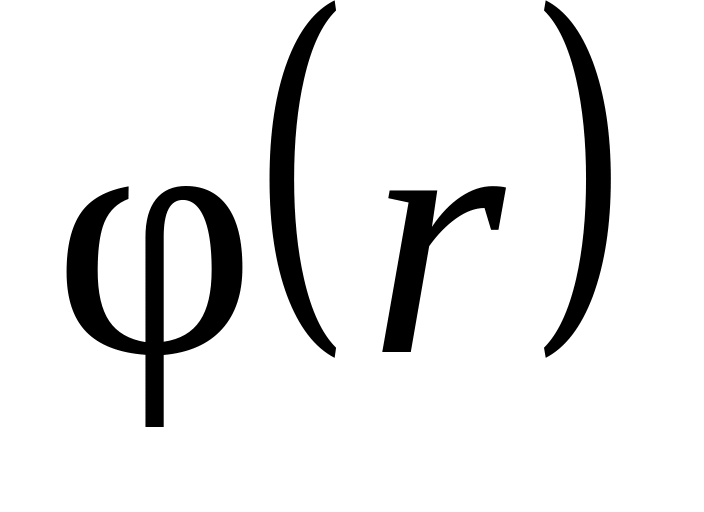 удовлетворяла заданным граничным
условиям. Во-первых, она должна стремиться
к нулю при
удовлетворяла заданным граничным
условиям. Во-первых, она должна стремиться
к нулю при
 .
Это условие выполняется только при
.
Это условие выполняется только при
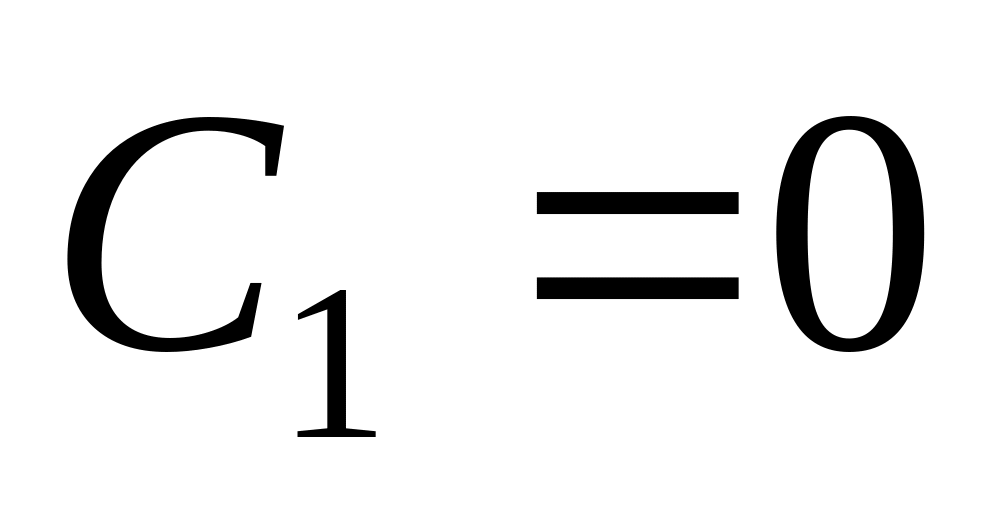 .
Во-вторых,
должна быть непрерывной функцией
координат, следовательно на поверхности
заряженного шара обе части функции (
и
)
должны принимать одинаковые значения:
.
Во-вторых,
должна быть непрерывной функцией
координат, следовательно на поверхности
заряженного шара обе части функции (
и
)
должны принимать одинаковые значения:
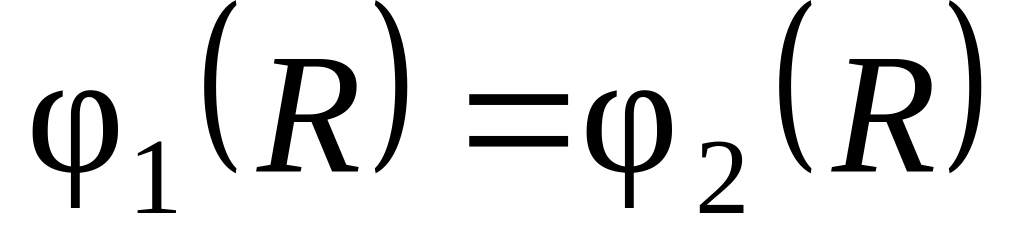 ,
или
,
или
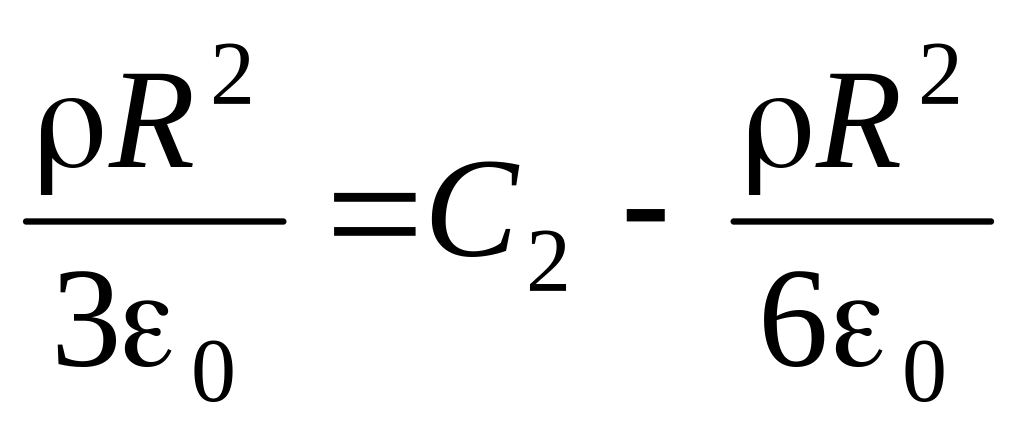 .
Из пос
.
Из пос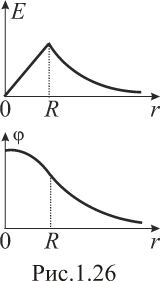 леднего
равенства следует, что
леднего
равенства следует, что
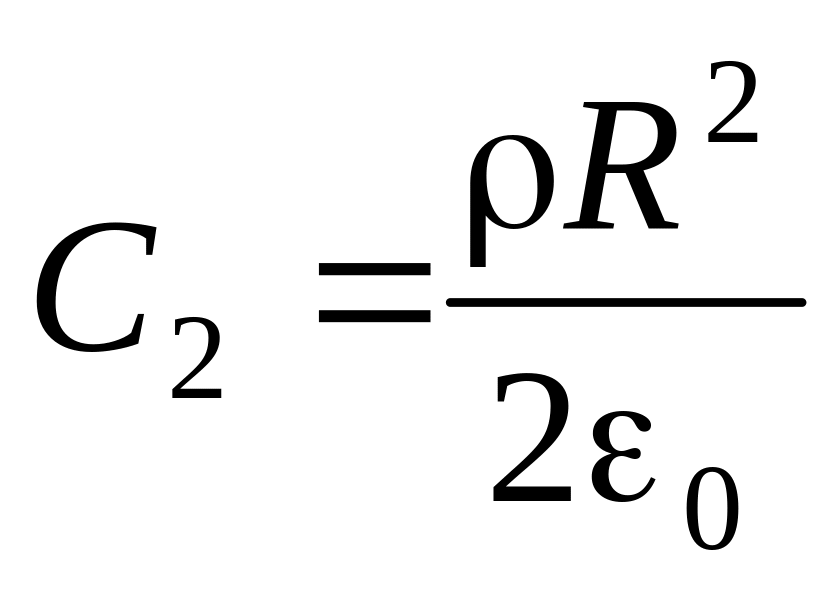 .
Таким образом, окончательно
.
Таким образом, окончательно
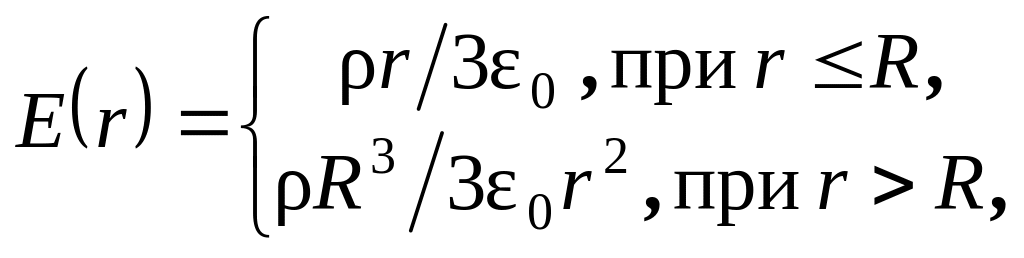
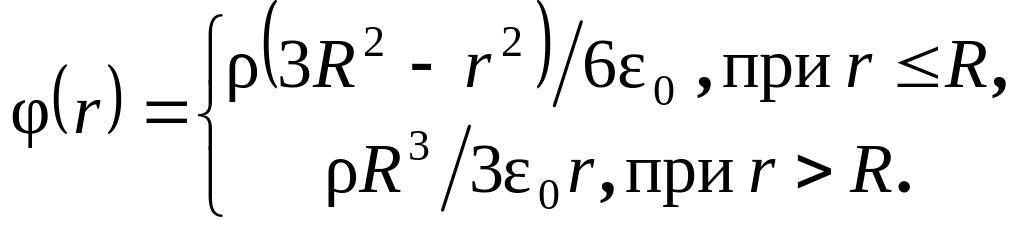 .
Графическое представление этих функций
см. на рис. 1.26.
.
Графическое представление этих функций
см. на рис. 1.26.
Задача 1.43
Условия
(1.2г) для компонентов поля
![]() и
и
![]() вблизи границы раздела вакуум-диэлектрик
при заданных углах
и
принимают вид:
вблизи границы раздела вакуум-диэлектрик
при заданных углах
и
принимают вид:
![]() и
и ![]() . (*)
. (*)
Решение системы (*) относительно неизвестных и тривиально и подробных комментариев не требует:
![]() ,
, ![]() В/м. (**)
В/м. (**)
Для того чтобы определить плотность связанных зарядов , появляющихся на поверхности диэлектрика в результате его поляризации, предварительно найдем нормальные компоненты вектора поляризованности . Проецируя первую из формул (1.2д) на нормаль к границе раздела и учитывая, что в вакууме значение параметра
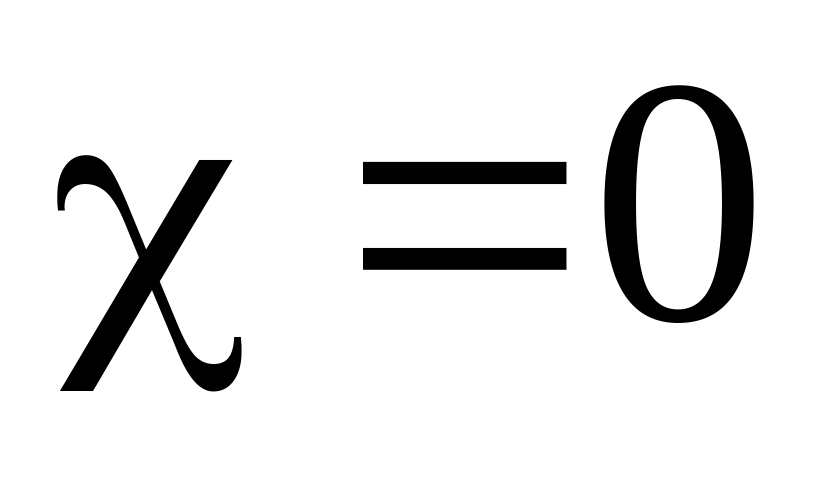 ,
получим
,
получим
 и
и
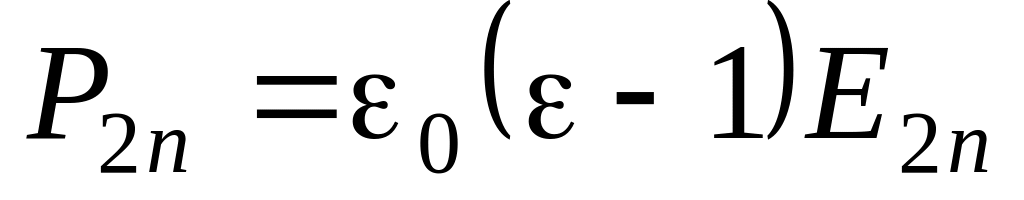 .
Как следует из (*),
.
Как следует из (*),
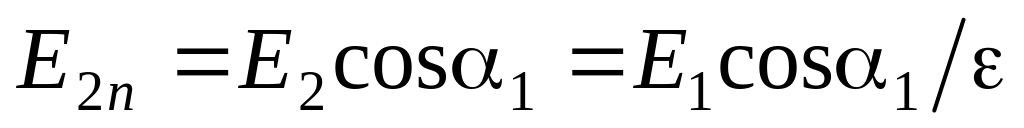 .
Поэтому
.
Поэтому
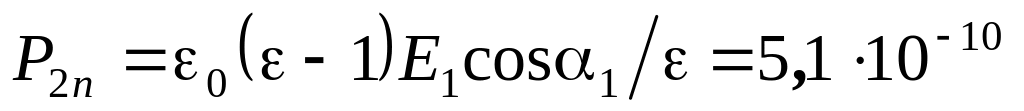 Кл/м2.
Кл/м2.Условия (1.2г) для компонентов
 позволяют вычислить
:
позволяют вычислить
:
![]() Кл/м2. (***)
Кл/м2. (***)
Знак этих зарядов отрицательный, как и должно быть, поскольку на них заканчивается часть силовых линий напряженности поля .
Задача 1.47
Из формул (1,2д)
следует, что поляризованность диэлектрика
и вектор электрического смещения
как функции координат имеют вид
![]() и
и
![]() .
В соответствии с (1.2в) объемные плотности
связанных и сторонних зарядов могут
быть найдены через дивергенции
соответствующих векторов:
.
В соответствии с (1.2в) объемные плотности
связанных и сторонних зарядов могут
быть найдены через дивергенции
соответствующих векторов:
![]() и, соответственно
и, соответственно
![]() .
.
Напомним, что
дивергенцией произвольной векторной
функции координат
![]() является сумма трех частных производных:
является сумма трех частных производных:
![]() .
Применив эту процедуру к векторным
функциям
и
,
получим соответственно
.
Применив эту процедуру к векторным
функциям
и
,
получим соответственно
![]() и
и
![]() .
.
Задача 1.51
Сторонние заряды в объеме стержня и на его поверхности отсутствуют; поэтому электрическое поле создается исключительно связанными зарядами. Выясним их расположение и величину.
Ввиду постоянства вектора по всему объему цилиндрического стержня
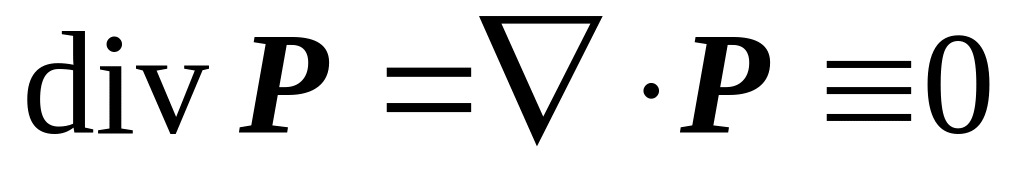 .
Следовательно, объемная плотность
связанных зарядов повсеместно в стержне
также равна нулю.
.
Следовательно, объемная плотность
связанных зарядов повсеместно в стержне
также равна нулю.
В соответствии с граничными условиями (1.2г) связанные заряды имеются только на торцах стержня, причем заряды положительного знака выступают на верхнем торце (их поверхностная плотность
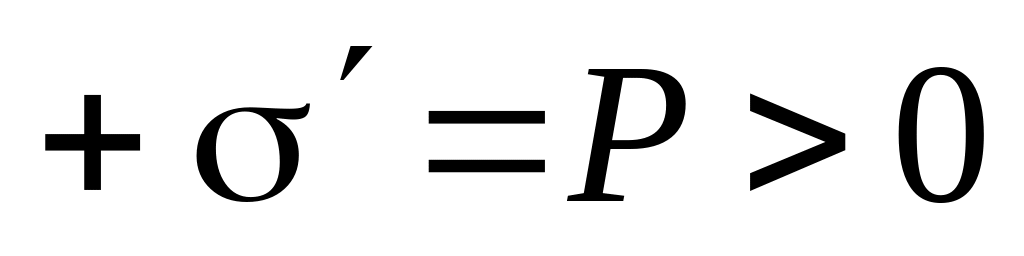 ).
Аналогично, на нижнем торце
).
Аналогично, на нижнем торце
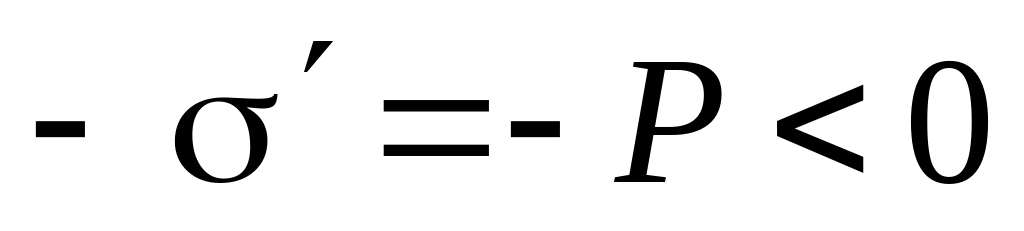 .
.Т
 аким
образом, электрическое поле создается
электронейтральной системой зарядов
аким
образом, электрическое поле создается
электронейтральной системой зарядов
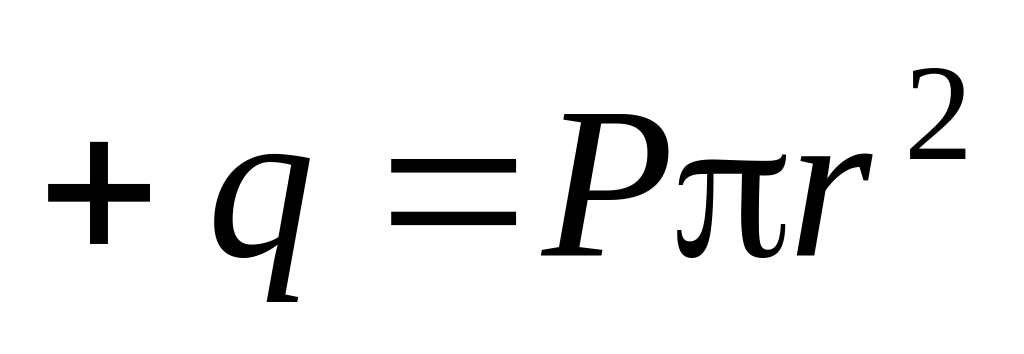 и
и
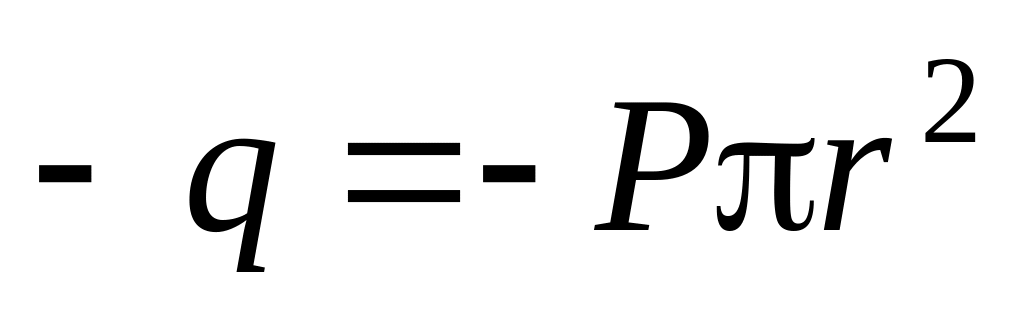 ,
находящихся на расстоянии
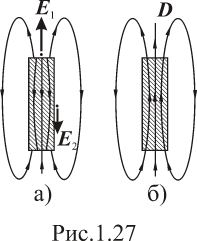
друг от друга. Вдали от торцов картина
силовых линий напряженности
напоминает поле электрического диполя
(рис.1.27,а). Подобную структуру имеют и
линии вектора электрического смещения
с тем отличием, что все эти линии
непрерывны (замыкаются сами на себя,
рис.1.27,б). Следует иметь в виду, что
внутри стержня векторы
,
и
связаны соотношением
,
находящихся на расстоянии
друг от друга. Вдали от торцов картина
силовых линий напряженности
напоминает поле электрического диполя
(рис.1.27,а). Подобную структуру имеют и
линии вектора электрического смещения
с тем отличием, что все эти линии
непрерывны (замыкаются сами на себя,
рис.1.27,б). Следует иметь в виду, что
внутри стержня векторы
,
и
связаны соотношением
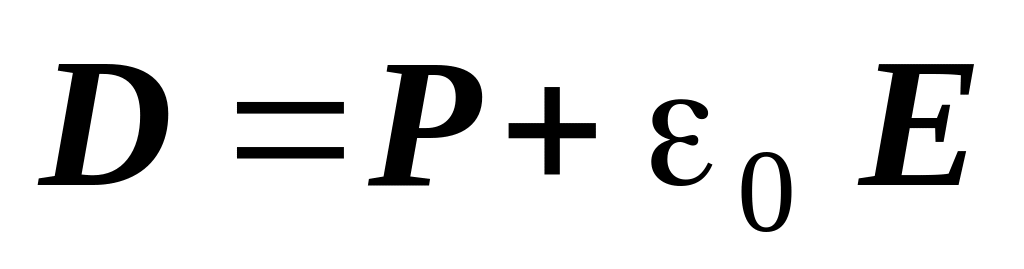 .
.При расчете величины напряженности поля в точках 1 и 2 (рис.1.14) учтем, что размеры стержня удовлетворяют условию
 .
Напряженность поля в точке 1, расположенной
в непосредственной близости от
«положительного» торца, вычисляется
как поле заряженной плоскости с
поверхностным зарядом
.
Напряженность поля в точке 1, расположенной
в непосредственной близости от
«положительного» торца, вычисляется
как поле заряженной плоскости с
поверхностным зарядом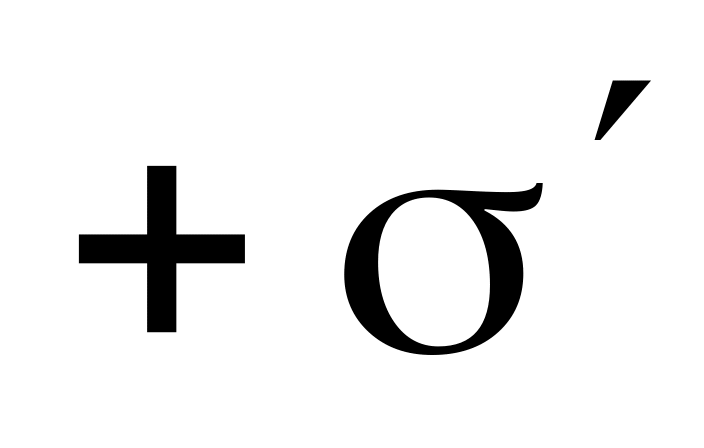 и равна
и равна
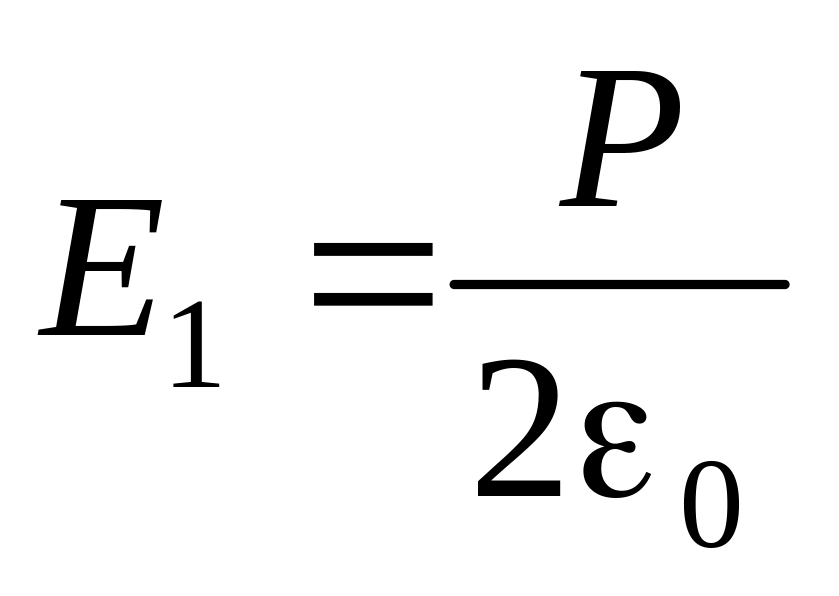 (см., например, задачу 1.4
или 1.27).
Вкладом удаленного «отрицательного»
торца можно пренебречь, поскольку его
можно рассматривать как точечный заряд
,
находящийся на удалении
от точки 1. Модуль напряженности поля
этого заряда
(см., например, задачу 1.4
или 1.27).
Вкладом удаленного «отрицательного»
торца можно пренебречь, поскольку его
можно рассматривать как точечный заряд
,
находящийся на удалении
от точки 1. Модуль напряженности поля
этого заряда
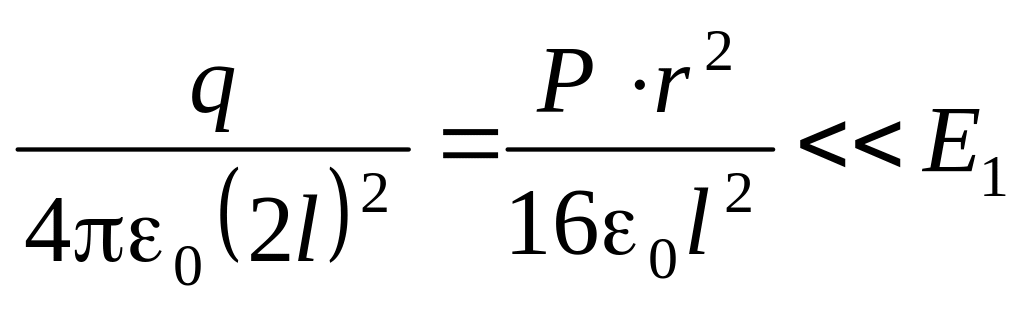 .
В равноудаленной от торцов точке 2
напряженность поля можно вычислять
как скалярную сумму полей точечных
зарядов
и
.
В равноудаленной от торцов точке 2
напряженность поля можно вычислять
как скалярную сумму полей точечных
зарядов
и
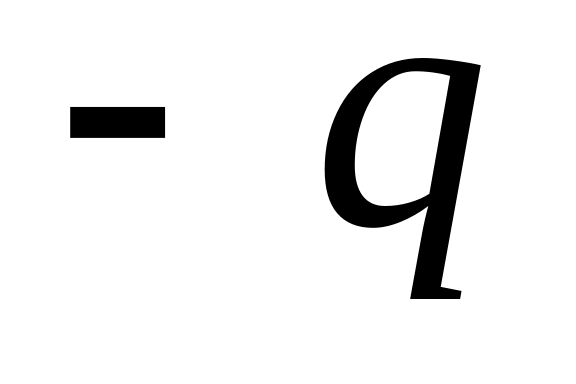 (рис.1.27,а):
(рис.1.27,а):
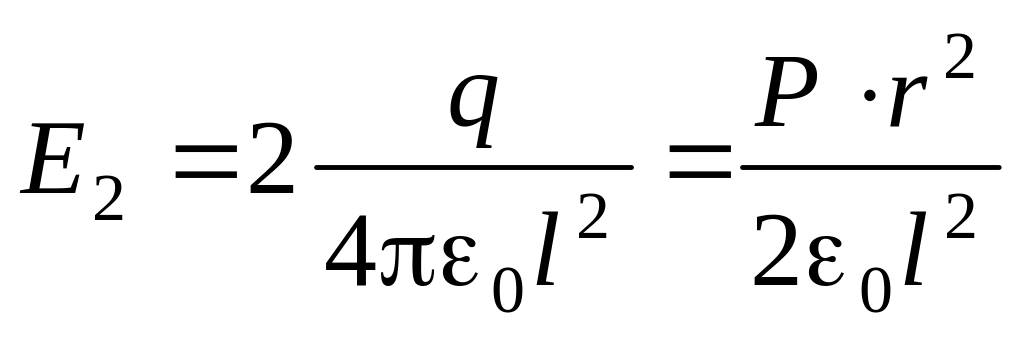 .
Векторы
и
антипараллельны :
.
Векторы
и
антипараллельны :
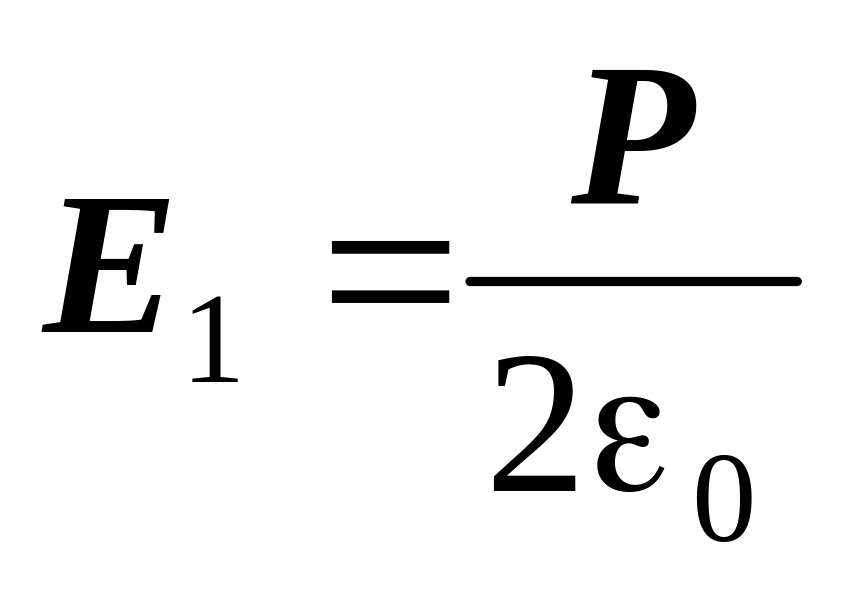 ,
,
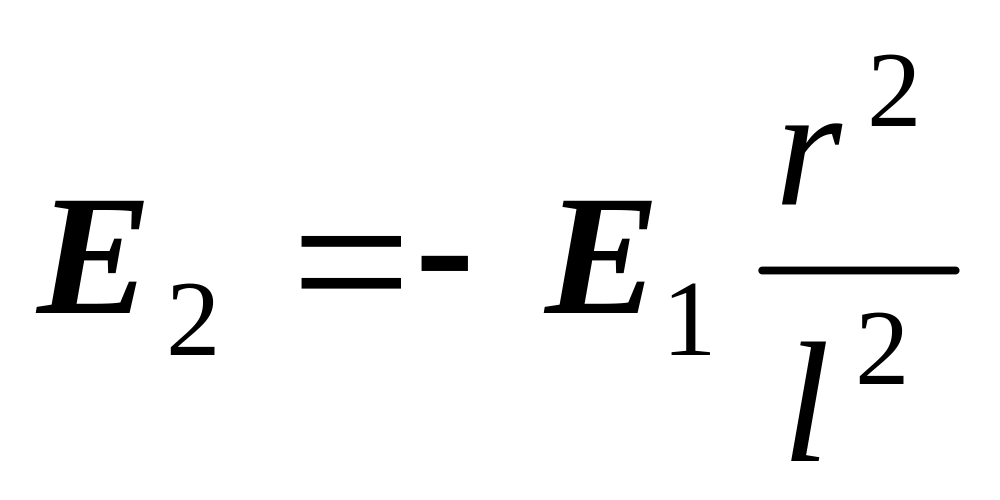 .
.
З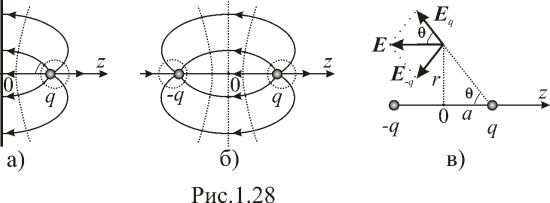 адача
1.55
адача
1.55
Рассмотрим поле
заряда
и металлической пластины (рис.1.28,а) и
сравним его с полем, создаваемым системой
точечных зарядов
и
,
находящихся на расстоянии
друг от друга (рис.1.28б).
В полупространстве
![]() эти поля идентичны. Объяснение этого
состоит в следующем. Плоскость
эти поля идентичны. Объяснение этого
состоит в следующем. Плоскость
![]() на рис. 1.28,б является, очевидно, одной
из эквипотенциальных поверхностей для
данной системы зарядов. Действительно,
все ее точки равноудалены от одинаковых
по величине разноименных зарядов и в
соответствии с принципом суперпозиции
потенциал любой из них
на рис. 1.28,б является, очевидно, одной
из эквипотенциальных поверхностей для
данной системы зарядов. Действительно,
все ее точки равноудалены от одинаковых
по величине разноименных зарядов и в
соответствии с принципом суперпозиции
потенциал любой из них
![]() .
Поэтому, если в плоскости
поместить тонкую проводящую пластину
с потенциалом, равным нулю, она не внесет
искажений в картину эквипотенциальных
поверхностей, изображенных на рисунке
пунктирными линиями. Следовательно, и
картина силовых линий не изменится, за
одним исключением: теперь силовые линии
будут замыкаться не на отрицательном
заряде
,
а на отрицательных зарядах, индуцированных
на поверхности пластины (рис.1.28,а).
.
Поэтому, если в плоскости
поместить тонкую проводящую пластину
с потенциалом, равным нулю, она не внесет
искажений в картину эквипотенциальных
поверхностей, изображенных на рисунке
пунктирными линиями. Следовательно, и
картина силовых линий не изменится, за
одним исключением: теперь силовые линии
будут замыкаться не на отрицательном
заряде
,
а на отрицательных зарядах, индуцированных
на поверхности пластины (рис.1.28,а).
Все вышеизложенное служит обоснованием так называемого метода зеркальных изображений. В этом методе (применительно к нашей задаче) вместо взаимодействия заряда и пластины рассматривается эквивалентное взаимодействие – между зарядами и . При этом заряд , служащий «заменой» для металлической пластины, называют изображающим зарядом.
В частности, сила электрического взаимодействия между зарядом и зарядами, индуцированными на пластине, может быть вычислена как сила взаимодействия между зарядами и :
![]() . (*)
. (*)
Аналогично энергия взаимодействия заряда и пластины равна
![]() . (**)
. (**)
Для выполнения третьей части задания – определения плотности зарядов, индуцированных на поверхности пластины, достаточно использовать соотношение (1.3а), которое в проекции на ось дает:
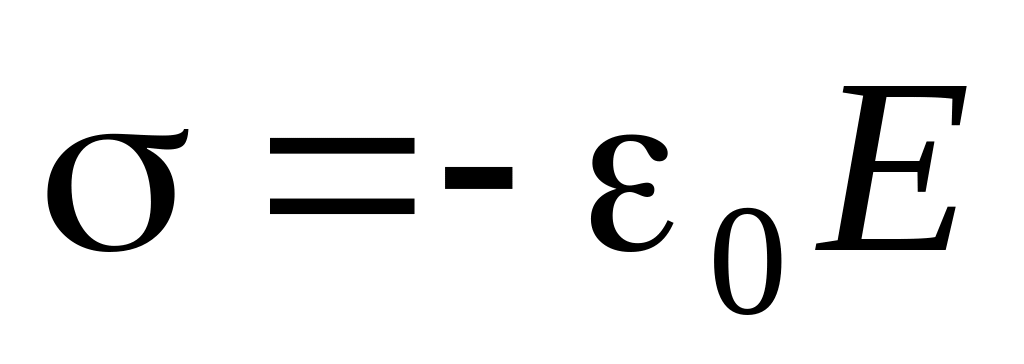 .
Вычисление напряженности поля
вблизи пластины как функции расстояния
от начала координат в рамках метода
зеркальных изображений проиллюстрировано
на рис.1.28,в. Используя принцип суперпозиции,
получим
.
Вычисление напряженности поля
вблизи пластины как функции расстояния
от начала координат в рамках метода
зеркальных изображений проиллюстрировано
на рис.1.28,в. Используя принцип суперпозиции,
получим
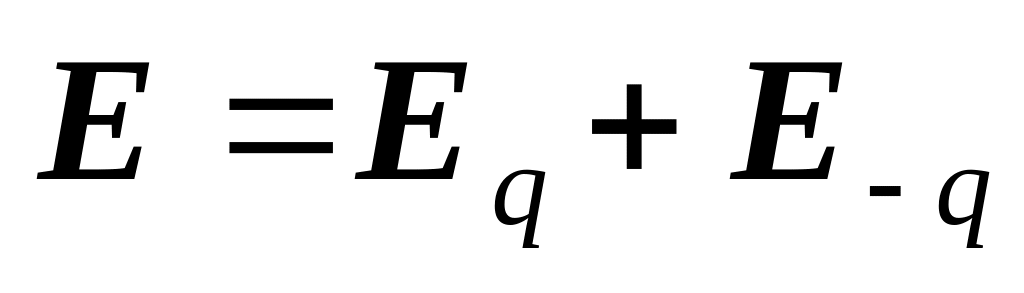 .
Отсюда следует, что
.
Отсюда следует, что
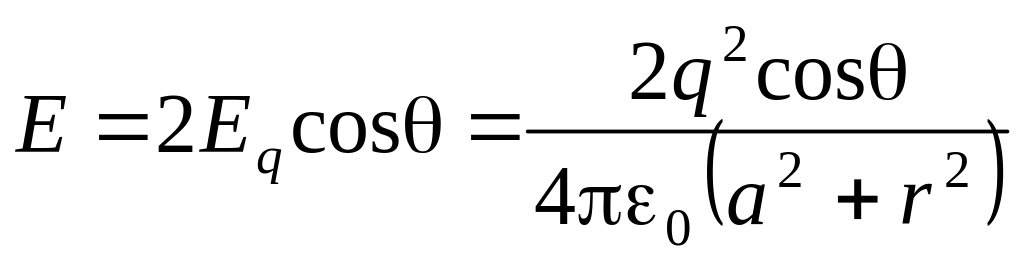 .
В свою очередь,
.
В свою очередь,
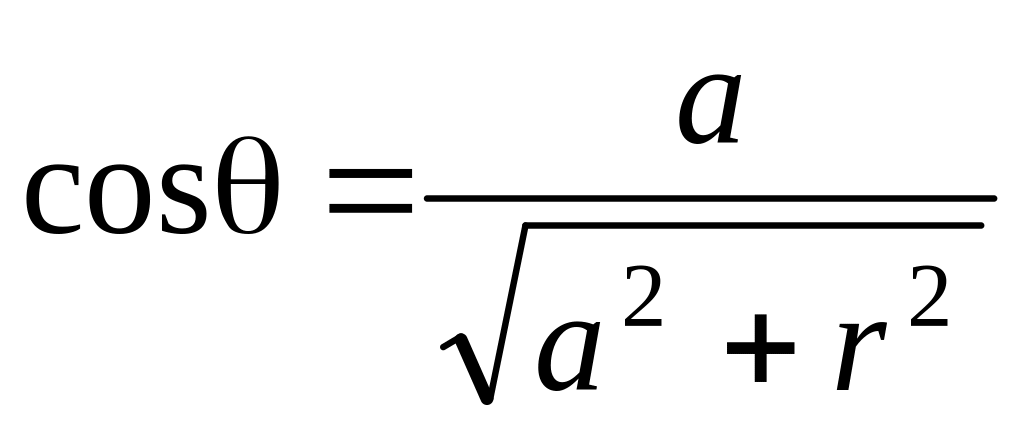 .
.
Объединив эти выражения, получим окончательно
![]() . (***)
. (***)
В заключение подчеркнем, что метод зеркальных изображений успешно применяется лишь в тех случаях, когда удается заменить проводящее тело такой системой изображающих зарядов, которая создавала бы поле с эквипотенциальной поверхностью, совпадающей с поверхностью изображаемого проводящего тела.
Задача 1.69
По определению (1.3в) емкость конденсатора
. (*)
Предположим, что известна величина стороннего заряда на его обкладках. Вычисление напряжения между обкладками конденсатора как функции этого заряда проводится в несколько этапов.
Н
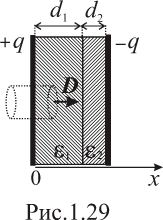 ачнем
с определения величины электрического
смещения
поля в конденсаторе, для чего используем
теорему Остроградского-Гаусса для
вектора
(формула 1.2б). Выберем замкнутую
цилиндрическую поверхность, один из
торцов которой расположен внутри, а
другой – вне пространства между
обкладками (рис.1.29). Будем считать,
что поле вектора
вне обкладок отсутствует, а между
обкладками оно однородно и направлено
вдоль оси
(рис.1.29). Тогда поток вектора
через выбранную поверхность состоит
лишь из потока через ее внутренний
торец:
ачнем
с определения величины электрического
смещения
поля в конденсаторе, для чего используем
теорему Остроградского-Гаусса для
вектора
(формула 1.2б). Выберем замкнутую
цилиндрическую поверхность, один из
торцов которой расположен внутри, а
другой – вне пространства между
обкладками (рис.1.29). Будем считать,
что поле вектора
вне обкладок отсутствует, а между
обкладками оно однородно и направлено
вдоль оси
(рис.1.29). Тогда поток вектора
через выбранную поверхность состоит
лишь из потока через ее внутренний
торец:
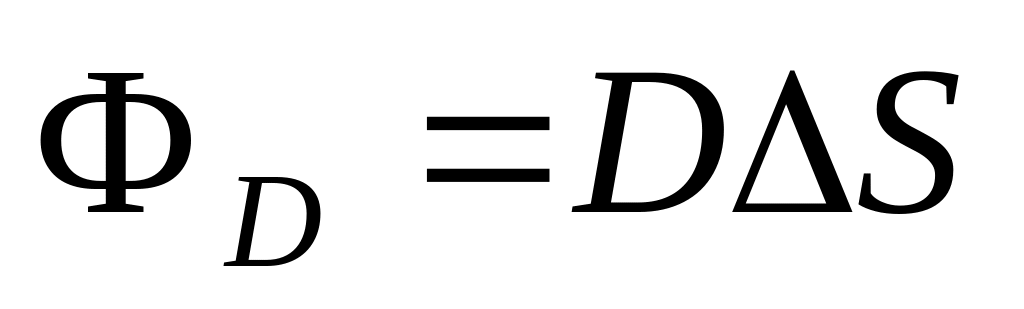 ,
где
,
где
 площадь торца. Количество стороннего
заряда внутри выбранной поверхности
также пропорционально площади торца:
площадь торца. Количество стороннего
заряда внутри выбранной поверхности
также пропорционально площади торца:
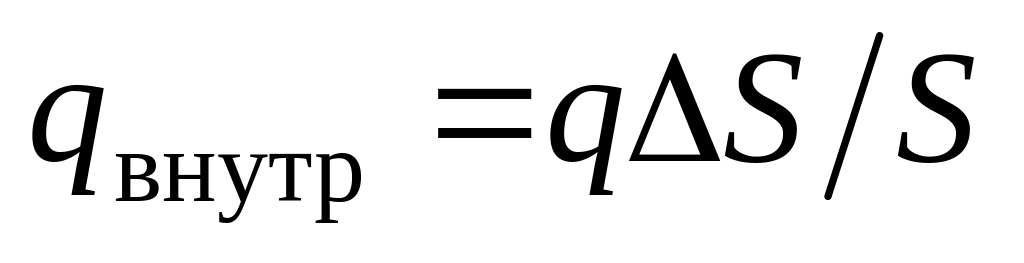 .
В соответствии с (1.2б) справедливо
равенство
.
В соответствии с (1.2б) справедливо
равенство
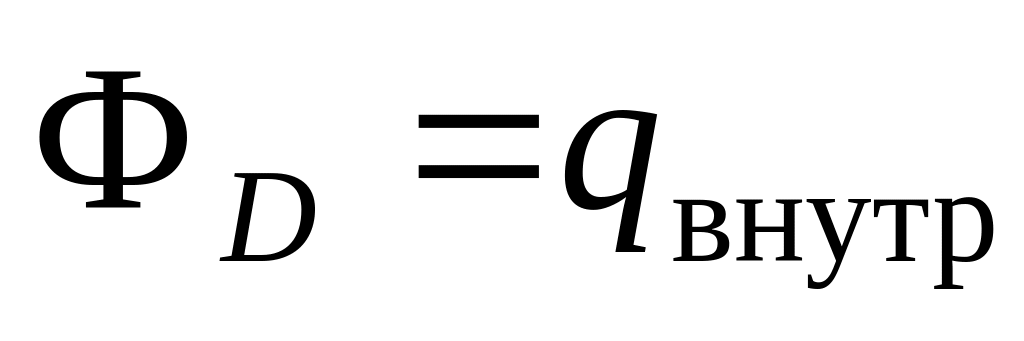 ,
из которого легко находим смещение
,
из которого легко находим смещение
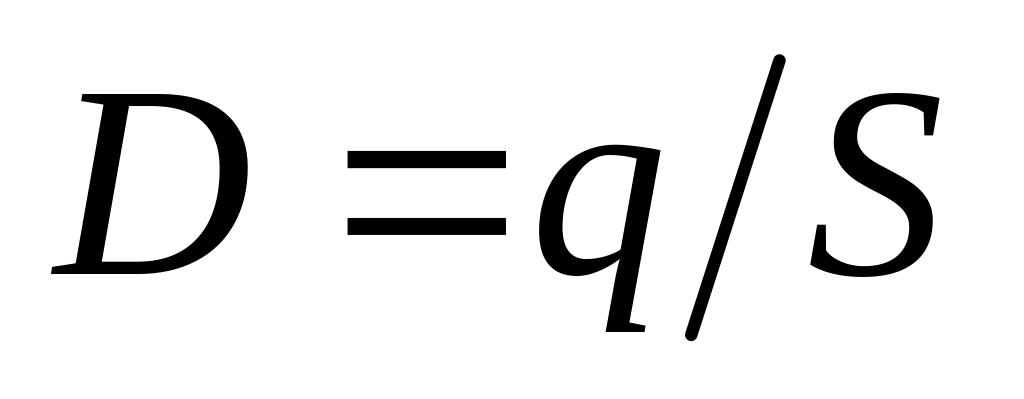 .
.Напряженность электрического поля как функцию найдем с помощью соотношения (1.2д):
![]() (**)
(**)
Очередной этап – определение напряжения между обкладками. Очевидно, его можно вычислить как сумму напряжений на двух однородных участках:
![]() . (***)
. (***)
Объединив выражения (*) – (***), получим
![]() .
Подстановка численных значений параметров
дает значение
.
Подстановка численных значений параметров
дает значение
![]() Ф.
Ф.
