Теоремы сложения и умножения вероятностей

Объединением (суммой) событий A₁, A₂, ..., A_n называется событие A, состоящее в наступлении хотя бы одного из этих событий. Обозначается одним из следующих способов

A = A₁ A₂ ... A_n  A₁ + A₂ + ... + A_n.

Пример. В урне 6 шаров, которые отличаются лишь номером i, . Событие A_i - наугад выбрать шар под номером i. Событие A = A₁ + A₃ + A₅ состоит в том, что будет выбран шар с номером 1 или 3 или 5, т.е. с нечетным номером.

Пересечением (произведением) событий A₁, A₂, ..., A_n называется событие B, состоящее в обязательном наступлении всех этих событий. Обозначается пересечение событий так

Пример. В урне 12 шаров, среди которых одна половина белых с номерами от 1 до 6, а другая черных с такими же номерами. Пусть A - "вынуть белый шар", B - " вынуть шар с нечетным номером. Тогда событие

C = AּB

означает " выбрать белый шар с нечетным номером".

События называются совместными, если они могут происходить одновременно. Несовместные события - это такие, которые не могут происходить одновременно.

Пример совместных событий:

А - "сегодня вторник",

В - "сегодня на улице идет дождь".

Пример несовместных событий:

D - "сейчас месяц сентябрь",

Е - "сейчас месяц декабрь".

А + В - "сегодня или вторник или на улице идет дождь",

D + T - "сейчас или сентябрь или декабрь".

Сформулируем основные теоремы.

Теорема 1. (сложение несовместных событий).

Если А и В - несовместные события, то

. (33)

Теорема 2. (сложение совместных событий).

Если А и В - совместные события, то

. (34)

В последней теореме встречается произведение событий АВ, которое означает одновременное наступление и события А и события В.

Например, если

А - "сегодня вторник",

В - "сегодня на улице идет дождь",

то событие АВ состоит в том, что "сегодня вторник и на улице идет дождь".

События А и В называются независимыми, если появление одного события не влияет на появление другого события. В приведенном выше примере события А и В - независимы.

События называются зависимыми, если появление одного события влияет на появление другого события.

Пример зависимых событий:

С - "сейчас март месяц",

F - "сегодня Международный женский день".

Для решения задач на нахождение вероятности произведения событий следует пользоваться следующими двумя теоремами:

Теорема 3. (умножение независимых событий).

Если А и В - независимые события, то

. (35)

Теорема 4. (умножение зависимых событий).

Если А и В - зависимые события, то

. (36)

В последней теореме встречается условное событие В|А, которое означает наступление В, при условии, что событие А уже наступило.

Например, если события

С - "сейчас март месяц",

F - "сегодня Международный женский день",

то

,

.

Воспользуемся теоремами 1 - 4 и формулами (33) - (36) для решения следующих задач:

Задача 1. Два охотника стреляют по одной мишени и имеют вероятности попадания 0,7 и 0,8 соответственно. Оба сделали по одному выстрелу. Какова вероятность того, что

а) в мишени ровно две пробоины,

б) в мишени хотя бы одна пробоина,

в) в мишени ровно одна пробоина?

Решение.

Введем обозначения: событие А - попал первый охотник, - первый охотник промахнулся, В - попал второй охотник, - второй охотник промахнулся, С - в мишени ровно две пробоины, D - в мишени хотя бы одна пробоина, Е - в мишени ровно одна пробоина. Очевидно, что

С = АВ, D = А + В, Е = A + B.

Действительно, событие С состоит в том, что произошло и событие А, и событие В одновременно, то есть произошло произведение событий АВ. Событие D состоит в том, что произошло хотя бы одно из событий А или В, то есть сумма событий А + В, и, наконец, событие С состоит в том, что А произошло а В нет или В произошло а А нет. Учитывая, что А и В независимые события (вероятность попадания одного из охотников не зависит от того попал другой или нет) и вероятности противоположных событий равны

Р ( ) = 1 - Р(А) = 0,3 и Р ( ) = 1 - Р(В) = 0,2 , получаем

Р(С) = 0,70,8 = 0,56 ,

Р(D) = Р(А) + Р(В) - Р(АВ) = 0,7 + 0,8 - 0,7х0,8 = 0,94 ,

Р(Е) = Р(А)Р( ) + Р( )Р(В) = 0,7х0,2 + 0,3х0,8 = 0,38.

Задание 10. Формула полной вероятности и формула Байеса

Теорема. Если событие А может наступить только совместно с появлением одного из событий некоторой полной группы несовместных событий (события этой группы называются гипотезами), то вероятность события А вычисляется по формуле полной вероятности

(34)

Или, кратко: , (34*)

где - вероятность гипотезы , - условная вероятность события А при условии осуществления гипотезы .

Задача 2. На фабрике, изготовляющей болты, первая машина производит 25 %, а вторая – 35 %, третья – 40 % всех изделий. В их продукции брак составляет соответственно 5, 4 и 2 %.

а) Какова вероятность того, что случайно выбранный болт дефектный?

в) Случайно выбранный из продукции болт оказался дефектным. Какова вероятность того, что он был произведен первой машиной?

Решение.

а) Обозначим за событие – болт сделан на первой машине, за событие – болт сделан на второй машине, за событие – болт сделан на третьей машине. Тогда:

– вероятность того, что болт сделан на первой машине. Соответственно .

Пусть событие А – болт бракован, тогда – вероятность, что брак выпущен первой машиной, соответственно .

Р(А) = 0,25 · 0,05 + 0,35 · 0,04 + + 0,40 · 0,02 + 0,0125 + 0,014 + 0,008 = 0,0345.

б) – вероятность того, что дефектный болт произведен первой машиной вычисляется по формуле Байеса, которая позволяет «пересмотреть» вероятности гипотез после того, как стало известно, что событие А наступило, т.е.:

. (35)

В нашем случае: .

Задание 11. Независимые испытания. Формула Бернулли

Пусть проводится п независимых испытаний (т.е. исход в каждом из испытаний не зависит от исходов в других испытаниях), вероятность появления события А в каждом из них неизменна и равна р. Тогда вероятность того, что в п испытаниях событие А появится ровно т раз определяется формулой Бернулли:

= , где . (36)

Задача 3. Что вероятнее выиграть у равносильного противника: а) три партии из четырех или пять из восьми; б) не менее трех партий из четырех или не менее пяти партий из восьми, если ничьих не бывает?

Решение.

Для равносильных противников вероятность выигрыша (проигрыша) одинакова, то есть .

а) Вероятность выигрыша m партий из n , т.е. задается формулой Бернулли

В первом случае n=4, m=3. Следовательно, вероятность выиграть три партии из четырех

.

Когда n=8, а m=5, то

.

Следовательно, .

б) Вероятность выиграть не менее трех партий есть сумма вероятностей выиграть три или четыре партии из четырех, так как эти события несовместны, то

.

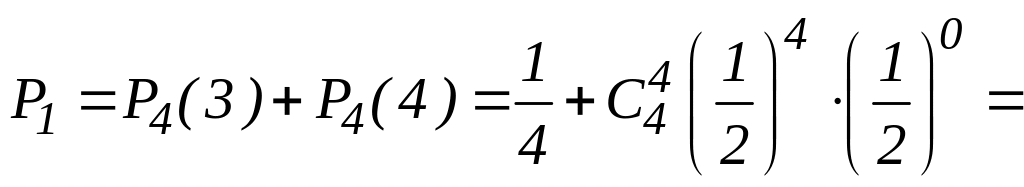
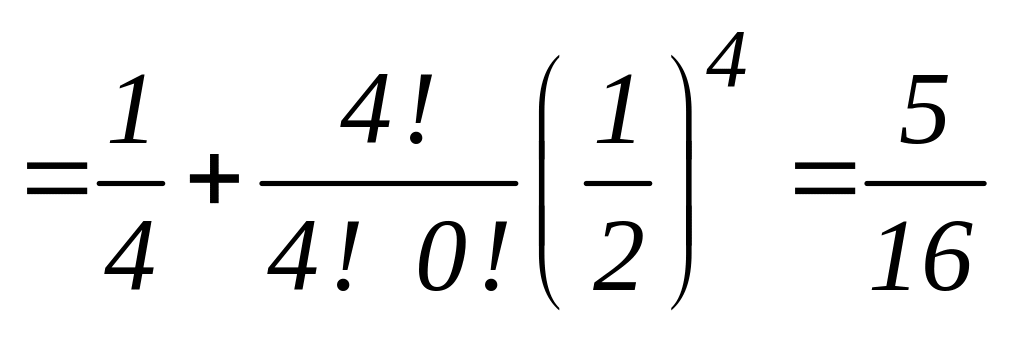(Напомним, что 0!=1).

Аналогично, вероятность выиграть не менее пяти партий из восьми

То есть, .

Следовательно, выиграть не менее пяти партий из восьми вероятнее.