
Лекция 9
Определение 1
Сумма
вида
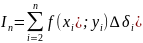 называется интегральной суммой для
функции z=f(x,y)
по области D
называется интегральной суммой для
функции z=f(x,y)
по области D
Определение 2
Двойным
интегралом от функции z=f(x,y)
по области D
называется предел её интегральной суммы
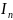 при стремлении max
из диаметров элементарной областей и
окружностью. Если этот предел существует
и конечен и не зависит от способа
разбиения области D
на элемент области
при стремлении max
из диаметров элементарной областей и
окружностью. Если этот предел существует
и конечен и не зависит от способа
разбиения области D
на элемент области
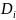 и способа выбора точки
и способа выбора точки

При этом пишут:

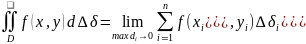 При
это называют:
При
это называют:
F(x,y) –подынтегральная функция
D-область интегрирования
Замечание:
Для обозначения двойного интеграла на
ряду с символом
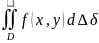 используется также и символ
используется также и символ
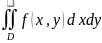
Теорема 1(о существовании двойного интеграла)
Если функция z=f(x,y) непрерывна в замкнутой области D, то двойной интеграл от этой функции по данной области существует.
Геометрический смысл двойного интеграла
Объём цилиндра с основанием двойного интеграла ограниченного сверху поверхностью z=f(x,y)
V=
Замечание: Функция z=f(x,y) должна быть не отрицательна и непрерывна в области D
Площадь плоской области D
S=
Основные свойства двойного интеграла
Двойной интеграл от суммы (разности) 2-х функций равен сумме (разности) 2-х интегралов от этих функций
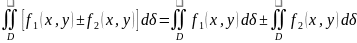
2)Const множитель можно выносить за знак двойного интеграла
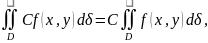 где
с-const
где
с-const
3)Если область интегрирования D разбита на 2 области D1 и D2, то
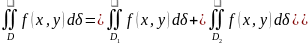
4)Если
всюду в D
f(x,y) ,
то
,
то
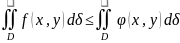 (при
условии, что эти интегралы существуют)
(при
условии, что эти интегралы существуют)
Вычисление Двойного интеграла в декартовой системе координат
Различают 2 основных вида области интегрирования
1)Область
интегрирования D
ограничен слева и справа прямыми x=a,
x=b
(a<b),
а снизу и сверху – непрерывными кривыми
y=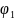 (x);
y=
(x);
y=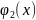
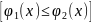 ,
каждая из которых пересекается
вертикальной прямой только в одной
точке. Для такой области ДИ вычисляется
по формуле
,
каждая из которых пересекается
вертикальной прямой только в одной
точке. Для такой области ДИ вычисляется
по формуле
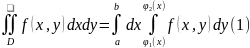 ,
где сначала вычисляется внутренний
интеграл, в котором x
считается постоянным
,
где сначала вычисляется внутренний
интеграл, в котором x
считается постоянным
2)Область
интегрирование D
ограничена снизу и сверху прямыми y=c,
y=d
(c<d)
А слева и справа непрерывными кривыми
x=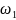 (y),
x=
(y),
x=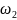 (y)
(y)
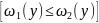 ,
каждая из которых пересекается с
горизонтальной прямой только в одной
точке. Для такой области Ди вычисляется
по формуле
,
каждая из которых пересекается с
горизонтальной прямой только в одной
точке. Для такой области Ди вычисляется
по формуле
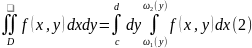 ,
где сначала вычисляется внутренний
интеграл, в котором y
считается постоянной
,
где сначала вычисляется внутренний
интеграл, в котором y
считается постоянной
Замечание: В более общем случаи область интегрирования путём разбиения на части сводится к основным областям
Определение 3
Правая часть формул (1) и (2) называются двукратными или повторными интегралами.
Лекция 10
Дифференциальным уравнением (ДУ) наз. уравнение, связывающее независимые переменные, их функцию и ее производные (или дифференциалы).
Если независимая переменная одна, то уравнение наз. обыкновенным, а если независимых переменных две или больше, то уравнение наз. ДУ в частных производных.
Порядком ДУ наз. порядок наивысшей производной, входящей в уравнение.
Решением ДУ наз. любая функция, которая при постановке в уравнение обращает его в тождество.
График решения ДУ наз. интегральной кривой.
Общий вид ДУ первого порядка F(x, y, y')=0.
Если ДУ F(x, y, y')=0 можно разрешить относительно y', то оно принимает вид y'=f(x, y) и наз. ДУ первого порядка, разрешенным относительно производной.
Общим решением ДУ первого порядка наз. решение этого уравнения, содержащее одну произвольную постоянную С, т.е. имеющие вид y= ϕ(x, C)
Замечание!:
если общее решение получается в неявной
форме
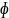 (x,
y, C)=0 или Ψ(x, y)=C, то оно наз. общим интегралом.
(x,
y, C)=0 или Ψ(x, y)=C, то оно наз. общим интегралом.
Решить или проинтегрировать данное ДУ значит найти его общее решение в той или иной форме.
Частным решением ДУ наз. решение, которое получается из общего решения при конкретном значении произвольной постоянной С.
Замечание: встречаются ДУ, имеющие такие решения, которые не получаются из общего ни при каком значении постоянной С (так называемые особые решения)
Задача,
в которой требуется найти частное
решение уравнения y'=f(x, y), удовлетворяющее
начальному условию y(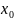 )=
)=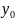 ,
где
,
-заданные
числа, наз. задачей Коши.
,
где
,
-заданные
числа, наз. задачей Коши.
Замечание: геометрически задача Коши означает, что ищется интегральная кривая, проходящая через заданную точку.
Т1 (о существовании и единственности решения задачи Коши)
Пусть
в прямоугольнике D={(x, y) ∈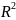 |
|x-
|≤a;
|y-
|≤b}
функция f(x, y) и ее частная производная
|
|x-
|≤a;
|y-
|≤b}
функция f(x, y) и ее частная производная
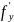 (x,
y) непрерывны. Тогда на некотором отрезке
[
-d,
+d]
существует единственное решение
уравнения y'=f(x, y), удовлетворяющее
начальному условию y(
)=
.
(x,
y) непрерывны. Тогда на некотором отрезке
[
-d,
+d]
существует единственное решение
уравнения y'=f(x, y), удовлетворяющее
начальному условию y(
)=
.
Замечание: геометрический смысл данной теоремы состоит в том, что через точку ( , )-центр прямоугольника, проходит одна и только одна интегральная кривая уравнения y'=f(x, y).
Уравнение вида ϕ(y)dy=f(x)dx наз. ДУ с разделенными переменными.
Замечание: в этом уравнении при дифференциале dx находится функция только от x, а при дифференциале dy находится функция только от y.
Метод решения ДУ с разделенными переменными заключается в непосредственном интегрировании обеих частей этого уравнения. Отсюда следует, что общий интеграл уравнения ϕ(y)dy=f(x)dx имеет вид ∫ϕ(y)dy=∫f(x)dx+С, где С - произвольная постоянная.
Уравнение вида y'=f(x)ϕ(y) наз. ДУ с разделяющимися переменными.
Замечание!:
ДУ с разделяющимися переменными может
быть записано также и в виде
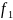 (x)
(y)dx+
(x)
(y)dx+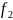 (x)
(x)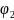 (y)dy=0.
При этом существенно, что коэффициенты
при дифференциалах распадаются на
множители, зависящие только от x или
только от y.
(y)dy=0.
При этом существенно, что коэффициенты
при дифференциалах распадаются на
множители, зависящие только от x или
только от y.
Метод решения ДУ с разделяющимися переменными основан на преобразовании данного уравнения к уравнению с разделенными переменными. Это достигается путем разделения переменных, т.е. путем деления обеих частей уравнения на произведение (y) (x).
Замечание!: деление на (y) (x) может привести к потере частных решений, которые обращают в нуль (y) (x), поэтому эти случаи нужно проверить отдельно.
Лекция 11
Функция
F(x, y) наз. однородной функцией степени
n, если для всех λ справедливо тождество
F(λx, λy) =
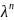 F(x,
y).
F(x,
y).
ДУ
первого порядка наз. однородным, если
оно может быть представлено в виде
y'=f( )
)
Замечание!: однородное ДУ может быть записано также и в виде M(x, y)dx+N(x, y)dy=0, где функции M(x, y) и N(x, y) являются однородными функциями одинаковой степени однородности.
Метод решения однородного ДУ основан на замене переменной y по формуле y=ux, где u-новая искомая функция от x. В результате такой замены однородное ДУ преобразуется в ДУ с разделяющимися переменными.
Уравнение вида y' + P(x) y = f(x) наз. линейным ДУ первого порядка.
Замечание!: название уравнения объясняется тем, что неизвестная функция y и ее производная y' входят в уравнение линейно, т.е. в первой степени.
Если f(x)≡0, то уравнение y' + P(x) y = f(x) наз. линейным однородным, в противном случае – линейным неоднородным.
Общее решение линейного однородного уравнения y' + P(x) y = 0 получается с помощью разделения переменных (т.к. данное уравнение является ДУ с разделяющимися переменными). Общее решение линейного неоднородного уравнения y' + P(x) y = f(x) можно найти исходя из общего решения соответствующего однородного уравнения методом вариации произвольной постоянной (методом Лагранжа). Сущность этого метода состоит в том, что в общем решении y= ϕ(x, C) соответствующего однородного уравнения произвольная постоянная C заменяется на новую неизвестную функцию С(х), которая находится путем подстановки функции y= ϕ(x, C(х)) в уравнение y' + P(x) y = f(x).
Лекция 12
Уравнение вида y''+py'+qy=0, где p и q – некоторые действительные числа, наз. линейным однородным ДУ.
Комплексным
числом наз. выражение вида z = a + ib, где а
и b – действительные числа, i-мнимая
единица, удовлетворяющая соотношению
 =-1.
Комплексные числа возникают в частности
в связи с задачей решения квадратного
уравнения, дискриминант которого меньше
нуля.
=-1.
Комплексные числа возникают в частности
в связи с задачей решения квадратного
уравнения, дискриминант которого меньше
нуля.
Метод решения линейного однородного ДУ второго порядка с постоянными коэффициентами основан на использовании так называемого характеристического уравнения.
Характеристическим
уравнением для уравнения y''+py'+qy=0 наз.
уравнение вида
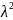 +pλ+q=0,
где λ - неизвестное число.
+pλ+q=0,
где λ - неизвестное число.
Замечание: характеристическое уравнение получается из уравнения y''+py'+qy=0 путем замены в нем: y'' на , y' на λ, y на 1.
Т1!(общее
решение линейного однородного ДУ второго
порядка с постоянными коэффициентами)
Пусть
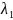 и
и
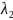 - корни характеристического уравнения
+pλ+q=0
соответствующего уравнения y''+py'+qy=0.
Тогда общее решение
уравнения y''+py'+qy=0 имеет вид:
- корни характеристического уравнения
+pλ+q=0
соответствующего уравнения y''+py'+qy=0.
Тогда общее решение
уравнения y''+py'+qy=0 имеет вид:
Если
корни
и
являются действительными и различными
числами
≠
),
то
=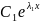 +
+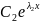
Если
корни
и
являются действительными и равными
числами
 ),
то
=
),
то
=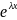 (
( +
+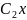 )
)
Если
корни
и
являются комплексными числами (
=
α + βi,
=
α − βi ), то
=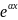 (
cosβx+
(
cosβx+
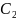 sinβx)
sinβx)
Здесь и - произвольные постоянные.
Уравнение вида y''+py'+qy=f(x), где p и q – некоторые действительные числа, f(x) – некоторая функция, наз. линейным неоднородным ДУ второго порядка с постоянными коэффициентами.
Метод решения уравнения y''+py'+qy=f(x) основан на следующей теореме:
Т2!( общее решение линейного неоднородного ДУ второго порядка с постоянными коэффициентами) Общее решение неоднородного уравнения y''+py'+qy=f(x) равно сумме общего решения соответствующего неоднородного уравнения и какого-либо частного решения данного неоднородного уравнения.
Замечание: для отыскания частного решения неоднородного уравнения y''+py'+qy=f(x) зачастую принимают метод подбора (метод неопределенных коэффициентов), суть которого состоит в том, что вид частного решения устанавливается по виду правой части уравнения и задача сводится к отысканию коэффициентов этого частного решения.
Рассмотрим различные виды правых частей уравнения y''+py'+qy=f(x), при которых возможно применять метод подбора.
Случай
1. Правая часть имеет вид f(x)=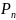 (x),
где
(x)-многочлен
степени n. Тогда частное решение ӯ можно
искать в виде ӯ=
(x),
где
(x)-многочлен
степени n. Тогда частное решение ӯ можно
искать в виде ӯ=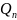 (x)
(x)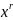 ,
где r-число корней характеристического
уравнения равных нулю,
(x)-полный
многочлен той же степени n, т.е. содержит
все степени x от 0 до n.
,
где r-число корней характеристического
уравнения равных нулю,
(x)-полный
многочлен той же степени n, т.е. содержит
все степени x от 0 до n.
Случай
2. Правая часть имеет вид f(x)=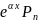 (x),
где
(x)-многочлен
степени n, α-известное действительное
число. Тогда частное решение ӯ следует
искать в виде ӯ=
(x),
где
(x)-многочлен
степени n, α-известное действительное
число. Тогда частное решение ӯ следует
искать в виде ӯ=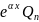 (x)
,
где
(x)-полный
многочлен той же степени n, r-число корней
характеристического уравнения равных
α.
(x)
,
где
(x)-полный
многочлен той же степени n, r-число корней
характеристического уравнения равных
α.
Случай
3. Правая часть имеет вид f(x)=acosβx+ bsinβx,
где a, b, β – известные действительные
числа, тогда частное решение ӯ надо
искать в виде ӯ=(Аcosβx+ Вsinβx)
,
где А,В – неизвестные коэффициенты,
r-число корней характеристического
уравнения равных
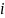 β.
β.
Случай
4. Общий вид правой части, при которой
возможно применять метод подбора
f(x)=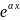 [
(x)cosβx+
[
(x)cosβx+
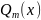 sinβx],
где
(x)-многочлен
степени n,
-многочлен
степени m, α и β – известные действительные
числа. Тогда частное решение ӯ следует
искать в виде ӯ=
[
sinβx],
где
(x)-многочлен
степени n,
-многочлен
степени m, α и β – известные действительные
числа. Тогда частное решение ӯ следует
искать в виде ӯ=
[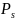 (x)cosβx+
(x)cosβx+
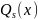 sinβx]
,
где r-число корней характеристического
уравнения равных α+
β,
(x)
и
-полные
многочлены степени s, s=max{n,m}.
sinβx]
,
где r-число корней характеристического
уравнения равных α+
β,
(x)
и
-полные
многочлены степени s, s=max{n,m}.
Замечание:
Если y''+py'+qy=
(x)+
(x),
то частное решение можно искать в виде
ӯ= +
+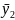 ,
где
-частное
решение уравнения y''+py'+qy=
(x),
-
частное решение уравнения y''+py'+qy=
(x)
,
где
-частное
решение уравнения y''+py'+qy=
(x),
-
частное решение уравнения y''+py'+qy=
(x)
