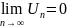Математический Анализ

Лекция 1

Определение 1

Пусть дана числовая последовательность u1, u2, u3, …un,… выражение вида u1+u2+u3+..+un…=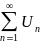 называется числовым рядом или просто рядом. При этом числа u1, u2, u3, …un,… называются членами ряда , а un называется общим членом ряда.

Ряд называется заданным, если известен его общий член, то есть если задана функция F(n) от натурального аргумента n.

Определение 2

Сумма n первых членов ряда Sn называется n-ой частичной суммой ряда.

Замечание !

Так как число членов ряда бесконечна, то частичные суммы ряда образуют бесконечную последовательность частичных сумм.

S1, S2, S3,…Sn,…

Определение 3

Ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм т.е. 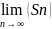=S.

При этом число S называется суммой ряда и пишут вида u1+u2+u3+..+un…=S или =S

Определение 4

Геометрическим рядом называется ряд , составленный из членов геометрической прогрессии:

a+aq+aq2+aq3+…aqn-1 +…= , где а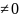

Вывод

Геометрический ряд сходится к сумме 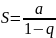, при и расходится при .

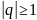Свойства сходящихся рядов

1. Если ряд u₁+u₂+u₃+..+u_n…сходится и имеет сумму S , то и ряд

au₁+au₂+au₃+…+au_n…, который получился путем умножения данного ряда на число а. Также сходится и имеет сумму аS.

2. Если ряды u₁+u₂+u₃+..+u_n… и v₁+v₂+v₃+…+v_n+… сходится и их суммы соответственно равны S₁ и S₂

Определение 5

Ряд u_n+1+u_n+2+u_n+3+… ,полученный из ряда суммы по , путем отбрасывания его первых n членов называется n-ым остатком ряда и обозначается символом R_n.

Замечание

Сумму S можно представить в виде S=S_n+R_n, где

S_n - n-ая частичная сумма ряда

R_n – n-ый остаток ряда

Теорема 1

Ряд и любой его остаток одновременно сходятся , либо одновременно расходятся .

Теорема 2(Необходимый признак сходимости)

Если ряд сходится, то предел его общего члена стремится к нулю, то есть

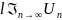
Замечание

Для вычисления пределов числовых последовательностей (функций натурального аргумента) часто применяют следующую теорему.

Теорема 3(О “Погружении" дискретного аргумента n в непрерывный (x) )

Если 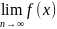существует и равен А, то 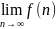также существует и равен А.

Лекция 2

Теорема 1 (1-ый признак сходимости)

Пусть даны 2 ряда с положительными членам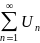и и ,

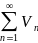Причем каждый член первого ряда не превосходит соответствующего члена второго ряда т.е. 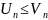(n=1,2,3,…), тогда:

1. Если сходится ряд , то сходится и

2. Если расходится ряд , то расходится и ряд

Замечание

Этот признак остается в силе, если неравенство . выполняется не при всех n, а лишь с некоторого номера n=N

Замечание!

В качестве рядов для сравнения часто используют следующие ''эталонные '' ряды.

1. Геометрический ряд 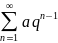, который сходится при и расходится при

2. Гармонический ряд , который расходится

3. Обобщенный гармонический ряд (Ряд Дирихле) 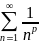, который сходится при 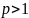и расходится при

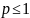
Теорема 2 ( 2ой предельный признак сравнения )

Пусть 2 ряда с положительными членами и и существует конечный предел отношения их общих членов

, то ряды одновременно сходятся, либо одновременно расходятся.

Теорема 3 (Признак Даламбера)

Если дан ряд с положительными членами и существует предел 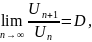тогда

1. Ряд сходится, если

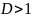
2. Ряд расходится, если

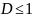
Замечание

Если D=1, то ряд может, как сходится, так и расходится. В этом случае необходимо дополнительное исследование ряда с помощью других признаков.

Теорема 4 (Признак Коши)

Пусть дан ряд с положительными членами и существует предел 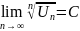, тогда

1. Ряд сходится, если

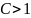
2. Ряд расходится, если

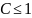
Замечание

Если C=1, то вопрос о сходимости ряда остается открытым.

Теорема 5 (Интегральный признак Коши)

Пусть функция f(x) на промежутке 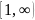удовлетворяет условиям

1. Положительна

2. Убывает

3. Непрерывна

Тогда ряд 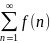и несобственный интеграл 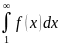одновременно сходятся либо одновременно расходятся.

Замечание

Интегральный признак остается в силе, если нижний предел в несобственном интеграле равен а ( )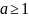

Определение 1

Пусть n некоторое натуральное число, тогда число 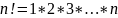называется n факториал. При этом по определению полагают

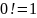
Лекция 3

Определение 1

Знакочередующимся рядом называется ряд в котором члены попеременно, то положительны, то отрицательны .То есть ряд вида:

u₁-u₂+u₃-u₄+u₅-…+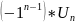 +…= 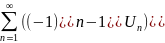, где

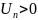(n=1,2,3,…)

Теорема 1 (Признак Лейбница сходимости знакочередующегося ряда)

Знакочередующийся ряд сходится, если абсолютные величины его членов монотонно убывает, а общий член стремится к нулю, т.е. если выполняются следующие 2 условия :

1. 

2. 

Замечание

Признак Лейбница справедлив, если неравенство

выполняется с некоторого N.

Определение 2

Ряд с членами произвольных знаков называется знакопеременными.

Замечание

В знакопеременном ряде члены могут быть как положительными, так и отрицательными, причем их расположение в ряде произвольна, при этом знакочередующийся ряд является частным случаем знакопеременного ряда.

Теорема 2(Признак сходимости знакопеременного ряда)

Если ряд 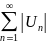сходится, то сходится и ряд

Замечание

Из сходимости ряда не следует (вообще говоря) сходимости ряда

Определение 3

Знакопеременный ряд называется абсолютно сходящейся, если сходится ряд из абсолютных величин его членов.

Определение 4

Знакопеременный ряд называется условно сходящимся, если он сходится, а ряд из абсолютных величин его членов расходится.

Замечание

Так как ряд, составленный из абсолютных величин, является рядом с положительными членами, то для исследования вопросов о его сходимости можно применять рассмотренные ранее в лекции 2 признаки сходимости, признаки сравнения, признак Даламбера, признаки Коши.

Метод математической индукции

Пусть N множество натуральных чисел и A(n) некоторое зависящее от

утверждение, от если

1. Доказано, что утверждение А(1) верно

2. При условии, что утверждение А(n) верно для некоторого n, доказано что утверждение, от A(n+1) также верно

Тогда утверждение A(n+1) верно для всех