46. Разложение в ряд Фурье четных и нечетных функций.

f(x) – четная, =>

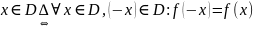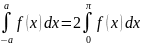
f(x) – нечетная,

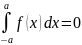
1. Пусть f(x) – четная =>

а) f(x)cosnx – четная

б) f(x)sinnx – нечетная

коэффициенты для четного ряда фурье:

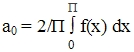
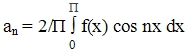
b_n=0

2. Пусть f(x) – нечетная =>

а) f(x)cosnx – нечетная

б) f(x)sinnx – четная

коэффициенты для нечетного ряда фурье

a₀=0

a_n=0

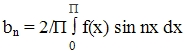
47. Разложение в ряд Фурье функций произвольного периода.

Рассмотрим кусочно-непрерывную f (x), заданную в интервале [− l, l]. Используя подстановку

x=lt/пи

t=пи*х/l

x [-l;l]

t [-пи;пи]

f(x)=f(lt/пи)=φ(t) (T=2l)

определенную и интегрируемую в интервале [−π, π]. Разложение в ряд Фурье для функции F (y) имеет вид

φ(t)=a₀/2+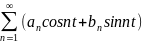

Коэффициэнты Фурье для данной функции определяются формулами

a₀=1/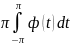

a_n=1/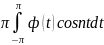

b_n=1/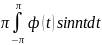

Возвращаясь к первоначальным переменным, то есть полагая t=пи*х/l, получим следующие выражения для ряда Фурье исходной функции f (x):

φ(t)=a₀/2+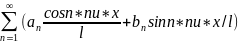 , где

a₀=1/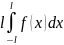

a_n=1/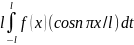

b_n=1/

49. Основные формулы комбинаторики.

Перестановкой из н-элементов называется всевозможные комбинации из этих элементов отличающиеся порядком.

Pn=n! – число перестановок без повт

Pn=n!/n1!*n2!*...*nk – с повт

Размещением из н-элементов по к-элементов называется комбинацией состоящяя из к-элементов, отличающаяся составом комбинаций и порядком элементов.

Ak_n=n!/(n-k)! – число размещений без повт

Ak_n=n^k – с повт

Сочетанием из н по к элементов назыв всевозможные комбинации из к элементов которые отличаются только составом комбинаций (порядок не важен)

Ck_n=n!/k!(n-k)!

Правило суммы: если объект А из некторой совокупности можно выбрать н-способами, а объект б – м-способами, то выбрать А или Б – н+м

Правило произведения: А и Б – н*м

50. Событие и вероятность. Классификация событий. Алгебра событий.

Событием называется рез-тат испытания (опыта).

Испытанием называется осуществление опр комплекса условий.

Достоверным событием называется которое обязат произойдет в рез-тате испытания.

Невозможным – никогда не наступит в рез-тате испытания.

Случайным – которое в рез-тате испытания может наступить или нет.

А, В, С – события.

Два события А и В назыв несовместными, если появление одного из них искл появл другого, в противном случае они совместны.

н-событий А1 А2 А3 Ан образуют полную группу если появление хотя бы 1 из них есть событие достоверное.

А, В – равновозможные если нет оснований считать ни одного из них более возможным чем другое.

А+В – событие, состоящее или в появлении события А иои В или в их совместном появлении.

А*В – событие, состоящее в совместном появлении события А и В.

Противоположными событиями назыв два единственно возможных события, образующих полную группу.

Элементарным исходом называется каждый рез-тат испытания.

А - {вытащил йух из штанов}

Благоприятствующим данному событию назыв элементарные исходы при которых событие наступило.

51. Классическое определение вероятности. Геометрическая вероятность.

Вероятностью события А – Р(А)=м\н, где м – число благоприятствующих данному событию элементарных исходов, н – общее число элемент исходов.

Св-ва вероятностей: если А – достоверно Р(А)=1, невозможно =0, случайно – от 0 до 1.

Относительной частотой события А – W(A) – назыв отношение числа опытов, в результате которых произошло событие А к общему числу опытов.

W(A)=m/n

Статистической вероятностью события А назыв относительная частота этого события.

P(A)=W(A) при бесконечном кол-ве испытаний.

Геом. вероятность:

Пусть отрезок l составляет часть отрезка L. На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством

Р = Длина l / Длина L.

Пусть плоская фигура g составляет часть плоской фигуры G. На фигуру G наудачу брошена точка. Это означает выполнение следующих предположений: брошенная точка может оказаться в любой точке фигуры G, вероятность попадания брошенной точки на фигуру g пропорциональна площади этой фигуры и не зависит ни от ее расположения относительно G, ни от формы g. В этих предположениях вероятность попадания точки в фигуру g определяется равенством

Р = Площадь g / Площадь G.

Р = mes g / mes G. – mes – мера

Два лица и условились встретиться в определённом месте между двумя и тремя часами дня. Пришедший первым ждет другого в течение 10 минут, после чего уходит. Чему равна вероятность встречи этих лиц, если каждый из них может прийти в любое время в течение указанного часа независимо от другого?

Решение. Будем считать интервал с 14 до 15 часов отрезком [0, 1] длиной в 1 час. Пусть («кси») и («эта») — моменты прихода и — точки отрезка [0, 1]. Все возможные результаты эксперимента — точки квадрата со стороной 1:

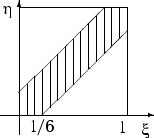
Можно считать, что эксперимент сводится к бросанию точки наудачу в квадрат. При этом благоприятными исходами являются точки множества :

(10 минут = 1/6 часа). Попадание в множество наудачу брошенной в квадрат точки означает, что и встретятся. Тогда вероятность встречи равна