38. Знакочередующиеся ряды. Признак Лейбница.

Знакочередующимся рядом называется ряд, у которого любые рядом стоящие члены имеют противоположные знаки.

Такие ряды удобнее записывать в виде

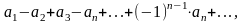(4.1)

или в виде

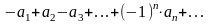, (4.2)

где

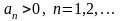
Для определения сходимости знакочередующихся рядов существует весьма простой достаточный признак.

Достаточный признак сходимости Лейбница

Для того чтобы знакочередующийся ряд (4.1)((4.2)) сходился, достаточно, чтобы абсолютные значения его членов убывали и стремились к нулю при возрастании n.

Таким образом, есл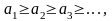и и 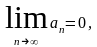то знакочередующийся ряд (4.1)((4.2)) сходится.

Док-во:

Рассмотрим последовательность частичных сумм с четными номерами

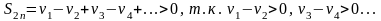(последовательность 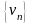монотонно убывает по условию теоремы).

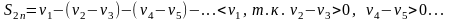
Т.е. последовательность 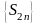ограничена сверху .

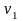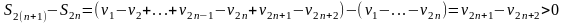
Т.е. последовательность монотонно возрастает.

По теореме Вейерштрасса существует .

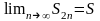Рассмотрим теперь последовательность частичных сумм с нечетными номерами

.

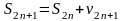По условию 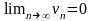, т.е. .

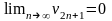По доказанному выше . Следовательно, предел правой части равенства сущест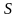вует и равен . Поэтому предел левой части равенства тоже существует и равен

.

Раскроем определение предела 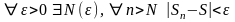как для четных n, так и для нечетных n. Следовательно, это справедливо для любых 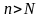, поэтому .

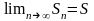Из доказанного выше неравенства 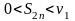. Переходя к пределу, получим .

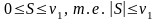Пример: ряд

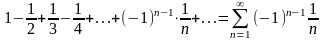
сходятся, т. к. для него выполняются все условия признака сходимости Лейбница.

39. Знакопеременные ряды. Абсолютная и условная сходимость.

(1) – знакоперемен, если среди его членов есть как + так и -.

Ряд (1) – абсолютно сход., если сходится ряд - 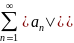(2)

ряд (1) – условно сход., если (2) – расх., а (1) – сход.

Т. Абсолютно сход ряд сходится (достаточное усл сходимости знакоперемен рядов)

если (2) – сх, (1) – сх.

Св-ва абсолютно сход. знакоперемен рядов:

1. абсолют сход ряды можно почленно складывать

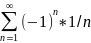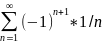= 0

= 0

2. у абсолютно сход ряда можно как угодно переставлять члены этого ряда, сумма от этого не изменится

40. Основные понятия степенного ряда.

Степенным рядом называется ряд вида:

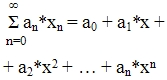(1)

a0, a1, a2, … - постоянные числа (действительные или комплексные) называются коэффициентами ряда (1), x - переменная степенного ряда.

Рассматриваем так же степенной ряд:

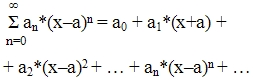(2)

Область сходимости степенного ряда:

Совокупность числовых значений аргумента x при которых ряд сходится называется его областью сходимости.

Теорема Абеля. Если степенной ряд (1) сходится в точке x0, то он абсолютно сходится в каждой точке x, для которой |x|<|x0|.

Следствие. Если ряд (1) расходится при х=х1, то он расходится и при всех х, для которых |x|>|x1|.

45. Тригонометрический ряд Фурье. Теорема Дерихле.

Рядом Фурье функции f(x) называется ряд:

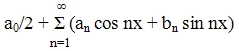- тригонометрический ряд

f(x) – периодичная

x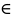 (-пи;+пи) – кусочно-непрерыв. имеет бесконечн. чисто точек разрыв 1 рода

f(x)=

Пусть функция f(x) - интегрируемая и периодическая с периодом 2П. a0, a1, a2, a3, …, an, …, b0, b1, b2, …, bn, … - коэффициенты Фурье функций f(x), которые находятся по формулам:

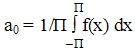
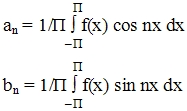
Свойства периодических функций:

1) Алгебраическая сумма периодических функций, имеющих один и тот же предел D, также есть периодическая функция с периодом T.

2) Если функция f(x) имеет период T, то функция f(a*x) имеет период T/a.

3) Если функция f(x) имеет период T и интегрируема на отрезке [x0;x1] прин. R, то интеграл 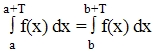для любых a,b прин. [x0;x1].

Теорема Дерихле.

1. Пусть f(x) – кусочно-непрерывная на x (-пи;+пи), периодическая, Т=2*пи

2. f(x) – кусочно-монотонна, x (-пи;+пи)

Ф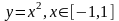 ункция f(x) называется кусочно-монотонной на отрезке [a,b], если этот отрезок можно разбить конечным числом точек на интервалы, в каждом из которых функция монотонна.

Примеры кусочно-монотонных функций:1) , 2)sinx, 3)cosx .

тогда ряд f(x)= с коэффициентами, построенный для этой функции сходится, и сумма его S(x):

а) в точках непрерывности = f(x)

б) если x0 – точка разрыва 1 рода – S(x0)=(f(x0-0)+f(x0+x))/2

в) на границах отрезка x=-пи, +пи

S(-П)=S(П)= (f(-П+0)+f(П-0))/2