
- •Двойной интеграл. Задачи, приводящие к понятию двойного интеграла.
- •22. Дифф ур-ия с разделяющимися переменными
- •25. Бернулли
- •29. Структура общего решения лнду -2.
- •30. Лоду с пост коэф.
- •31.Лнду с постоянными коэффициентами. Метод подбора.
- •33. Основные определения числового ряда.
- •34. Необходимый признак сходимости. Гармонический ряд.
- •35. Признаки сравнения.
- •36. Признак Даламбера.
- •37. Радикальный и интегральный признак Коши.
- •38. Знакочередующиеся ряды. Признак Лейбница.
- •39. Знакопеременные ряды. Абсолютная и условная сходимость.
- •40. Основные понятия степенного ряда.
- •45. Тригонометрический ряд Фурье. Теорема Дерихле.
- •46. Разложение в ряд Фурье четных и нечетных функций.
- •47. Разложение в ряд Фурье функций произвольного периода.
- •49. Основные формулы комбинаторики.
- •50. Событие и вероятность. Классификация событий. Алгебра событий.
- •51. Классическое определение вероятности. Геометрическая вероятность.
- •52. Теоремы сложения и умножения вероятностей. Следствия.
- •53. Формула полной вероятности.
- •54. Формула Байеса.
- •55. Формула Бернулли.
- •56. Теоремы Лапласа.
- •63. Функция распределения. Св-ва.
- •64. Плотность распределения и её св-ва.
- •66. Равномерное распределение.
- •67. Показательное (экспоненциальное) распределение.
- •68. Нормальное распределение.
Двойной интеграл. Задачи, приводящие к понятию двойного интеграла.
Об объеме цилиндрического тела.
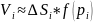

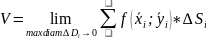
Опр: диаметром плоской фигуры (diam D) – называется наибольшее расстояние между 2 любыми точками этой фигуры, лежашей на границе фигуры D.
2. О массе тонкой пластины.
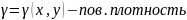

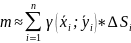 m=γ*ρ
m=γ*ρ

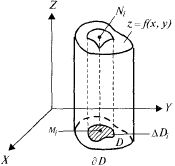
Алгоритм построения двойного интеграла.
Разобьём область D произвольно на n частей.
Обозначим площадь каждой ч/з ∆Di
Выберем

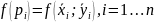 (найдём
значение функции в данной точке)
(найдём
значение функции в данной точке)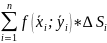 (Сложим
произведения высот (знач. ф-ии) на площадь
частички)
(Сложим
произведения высот (знач. ф-ии) на площадь
частички)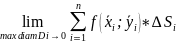 (устремляем
диаметр к 0)
(устремляем
диаметр к 0)
Определение двойного интеграла и его свойства.
Опр:
Если существует конечный предел ,
независящий ни от способа разбиения D
на части, ни от выбора Рi,
то этот предел называется двойным
интегралом от f(x;y) по области D.
,
независящий ни от способа разбиения D
на части, ни от выбора Рi,
то этот предел называется двойным
интегралом от f(x;y) по области D.
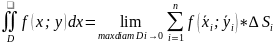
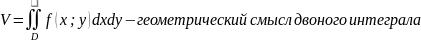
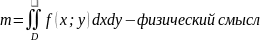
Свойства:
1)
2)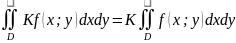
3)
D
= D1
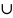 D2-
не
имеют
общих внешних точек
D2-
не
имеют
общих внешних точек
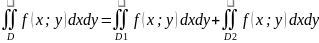
Повторный интеграл.
Опр:
повторным
интегралом от f(х;у)
по
правильной в направлении Оу области D
называется выражение вида:
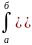
Вычисление двойного интеграла.
Опр: область D – правильная в направлении Ox, если любая прямая ǁ Ох проходящая ч/з внутреннюю точку пересекает границу области в 2-х точках.
Опр: область D – правильная в направлении Oу, если любая прямая ǁ Оу проходящая ч/з внутреннюю точку пересекает границу области в 2-х точках.

Замены переменных в 2-ом интеграле. 2-ой интеграл в полярных координатах.
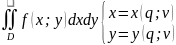 (1)
(1)
Опр:
определителем
Якоби (Якобианом)
для (1)
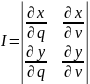
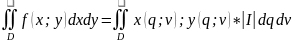 -формула
замены переменной
-формула
замены переменной
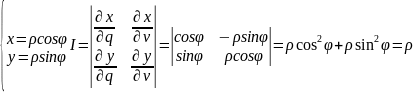
X2 + Y2 = ρ2=r2
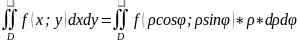 – в
полярных координатах.
– в
полярных координатах.
Выгодно если В – круг или часть круга.
Приложения двойного интеграла.
Задача (объём и масса)
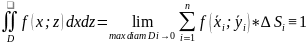
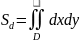 – площадь
плоского тела
– площадь
плоского тела
S пов-ти -
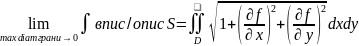
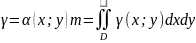
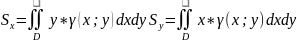 – статический
момент
– статический
момент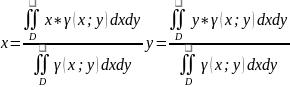 координаты
центра масс пластины.
координаты
центра масс пластины.
Задачи, приводящие к понятию криволинейного интеграла.
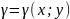
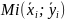
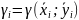
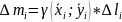
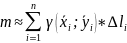
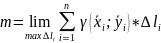 -
масса
кривой
-
масса
кривой
2) о работе переменной силы (2-го рода)
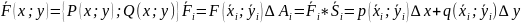
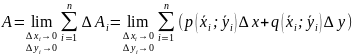
Определение и свойства криволинейного интеграла 1-го рода.
Опр:
если существует конечный предел
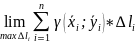 независящий ни от способа разбиения АВ
на части, ни от выбора промежуточных
точек, то этот предел – криволинейный
интеграл 1 рода.
независящий ни от способа разбиения АВ
на части, ни от выбора промежуточных
точек, то этот предел – криволинейный
интеграл 1 рода.
Свойства:
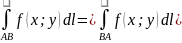 -
Интеграл не зависит от ориентации
кривой;
-
Интеграл не зависит от ориентации
кривой;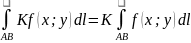
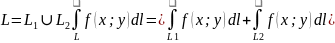
Вычисление криволинейного интеграла 1-го рода.
y=f(x;y); L:
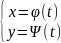 α≤t≤β
α≤t≤β
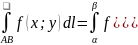 α≤β
α≤β
Y=ϕ(t) a≤x≤b
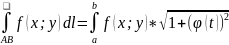 dx
a≤
b
dx
a≤
bΡ=ρ(ϕ) α≤ϕ≤β
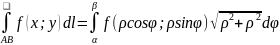 α≤β
α≤β
Определение и свойства криволинейного интеграла 2-го рода.
Опр:
Криволинейным
интегралом 2-го рода по
координатам
дуги является
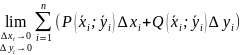 если
lim
не зависит ни от способа разбиения, ни
от Mi.
если
lim
не зависит ни от способа разбиения, ни
от Mi.

Замечание:
Q(x;y)≡0
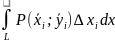
P(x;y) ≡0
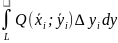
Свойства:
L = L1∩L2
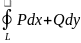 не
зависит от начала, зависит от направления.
не
зависит от начала, зависит от направления.
Вычисление криволинейного интеграла 2-го рода.
1)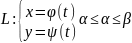
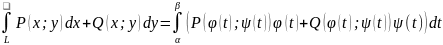
2)L: y=y(x) a≤x≤b

L: x=x(y) c≤y≤d
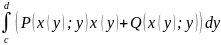
Формула Грина.
Данная формула устанавливает связь между двойным интегралом по области D и криволинейным интегралом по границе L. Пусть на оси Oxy задана область D, ограниченная прямой, параллельной плоскостям не более чем в двух точках (D - правильная область), тогда существует теорема.
P(x;y); Q(x;y). P.S. смотрим на изменения х и у при выборе пределов
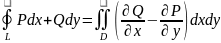
Приложения криволинейного интеграла 2о рода.
A~F
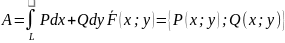
S плоской фигуры
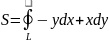
19. Формулы Стокса и Остроградского.
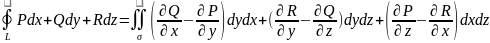 Стокс
Стокс
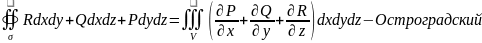
20. Задачи, приводящие к понятию диф.ур. 1 порядка.
1) скорость dS/dt=v(t) Лбобая производная по времени – скорость протекания процесса.
2) тангенс угла наклона касательной y`= tgα
21. Общие понятия дифф. Ур. 1 порядка.
Дифференциальное уравнение – уравнение содержащее неизвестную функцию, независимые переменные и производную от независимой функции.
Если неизвестная функция есть ф-я 1 переменной – то уравнение – обыкновенное дифференциально уравнение, если ФНП – диф. уравн в частных произв или ур-ие мат физики.
Порядком дифф ур-ия называется порядок наивысшей производной, входящей в это уравнение.
F(x;y;y2… y(n))=0 (1)
y(n)=f(x;y;y`... yn-1) (2)
F(x;y;y`)=0 (3)
y`=f(x;y) (4)
Условие
y(x0)=y0
(5) (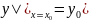 –
начальное
условие
для (3) и (4).
–
начальное
условие
для (3) и (4).
Решением (3) (4) y=ϕ(x),,, которая при подстановке обращает исходное в верное тождество.
Общим решением (3) (4) у=ϕ(х;С) зависящее от произвольной постоянной, удовл 2 условиям:
При любых С данное выр-ие есть решение уравнения
Какого бы не было (5) всегда можно подобрать С=С0, у=ϕ(х;С0) будет удовл данному начальному условию
Замечание: Ф(х,у,С)=0 – общий интеграл.
Частным решением ур-ия (3) (4) называется решение полученное из общего при конкретных значениях произвольной постоянной.
Задачей Коши для (4) называется задача нахождения частного решения, удовл данному условию.
