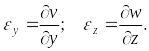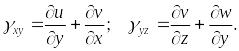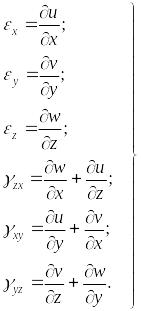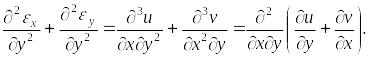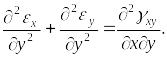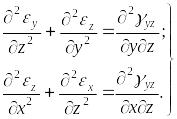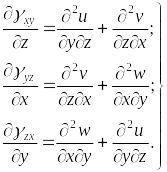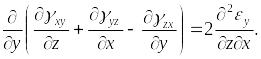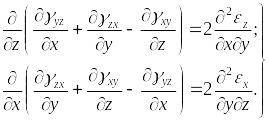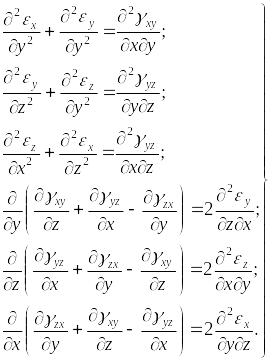18 Физический смысл уравнений неразрывности деформаций. Уравнения Коши для определения линейных и угловых деформаций.

Для определения деформации упругого тела сравним положения точек тела до и после приложения нагрузки.

Рассмотрим точку ненагруженного тела и ее новое положение после приложения нагрузки. Вектор называется вектором перемещения точки (рис.1.4).

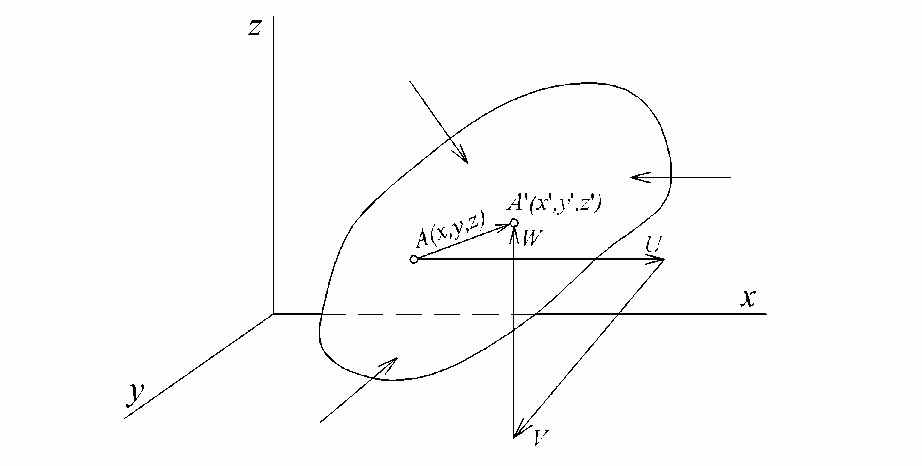
Рис.1.4. Вектор перемещения точки

Возможны два вида перемещений: перемещение всего тела как единого целого без деформирования — такие перемещения изучает теоретическая механика как перемещения абсолютно твердого тела, и перемещение, связанное с деформацией тела — такие перемещения изучает теория упругости.

Обозначим проекции вектора перемещения точки на координатные оси через соответственно. Они равны разности соответствующих координат точек и :

и являются функциями координат:

Деформирование тела вызвано разницей в перемещениях различных его точек. Бесконечно малый параллелепипед с ребрами вырезанный из упругого тела около произвольной точки , вследствие различных перемещений его точек деформируется таким образом, что изменяется длина его ребер и искажаются первоначально прямые углы между гранями.

На рис.1.5 показаны два ребра этого параллелепипеда: и длина ребра равна а ребра —

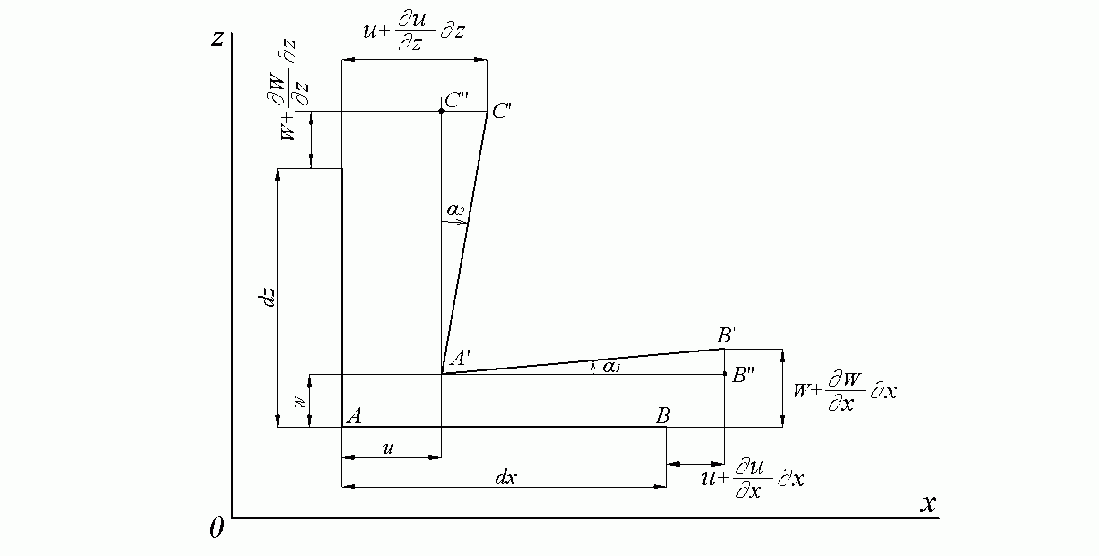
Рис.1.5. Линейные и угловые деформации

После деформации точки принимают положение При этом точка получит перемещение, составляющие которого в плоскости чертежа равны и Точка отстоящая от точки на бесконечно малом расстоянии получит перемещение, составляющие которого будут отличаться от составляющих перемещения точки на бесконечно малую величину за счет изменения координаты

Составляющие перемещения точки будут отличаться от составляющих перемещения точки на бесконечно малую величину за счет изменения координаты

Длина проекции ребра на ось после деформации:

(1.31)

Проекция абсолютного удлинения ребра на ось

Относительное удлинение вдоль оси

(1.32)

называется линейной деформацией по направлению оси .

Аналогично определяются линейные деформации по направлениям осей и

(1.33)

Рассмотрим изменение углов между ребрами параллелепипеда (рис.1.5). Тангенс угла поворота ребра в плоскости

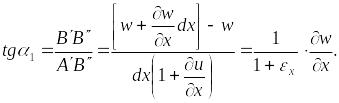
Вследствие малости деформаций а линейной деформацией можно пренебречь ввиду ее малости по сравнению с единицей, и тогда

Аналогичным образом можно определить угол поворота ребра в той же плоскости:

Искажение прямого угла называется угловой деформацией и определяется как сумма углов поворота ребер и :

(1.34)

Таким же образом определяются угловые деформации в двух других координатных плоскостях:

(1.35)

Формулы (1.32)-(1.35) дают шесть основных зависимостей для линейных и угловых деформаций от составляющих перемещения. Эти зависимости называются уравнениями Коши:

(1.36)

В пределе, когда длины ребер параллелепипеда стремятся к нулю, соотношения Коши определяют линейные и угловые деформации в окрестности точки

Положительным линейным деформациям соответствуют удлинения, а отрицательным — укорочения. Угол сдвига считается положительным при уменьшении угла между положительными направлениями соответствующих координатных осей и отрицательным — в противном случае

Соотношения Коши (1.36) связывают между собой шесть составляющих деформации и три составляющих перемещения, но эта связь не является взаимно однозначной. Если заданы три составляющих перемещения, то шесть составляющих деформации определяются однозначно. Если же заданы шесть составляющих деформации, то для определения трех составляющих перемещения нужно проинтегрировать шесть дифференциальных уравнений в частных производных. При произвольном выборе составляющих деформации шесть уравнений с тремя неизвестными не всегда могут быть решены однозначно, поэтому между шестью составляющими деформации должны существовать определенные зависимости.

Исключим составляющие перемещения из уравнений (1.36).

Дважды продифференцируем первое уравнение по а второе — по

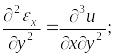
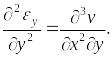
Сложим два последних выражения:

(1.41)

В скобках (1.41) записана угловая деформация и тогда

(1.42)

Аналогично для двух других координатных плоскостей

(1.43)

Уравнения (1.42), (1.43) означают, что если заданы две линейные деформации во взаимно перпендикулярных направлениях, то угловую деформацию в плоскости этих линейных деформаций нельзя задать произвольно. Для обеспечения однозначности решения этих уравнений недостаточно, так как они получены дифференцированием, а при этом порядок дифференциального уравнения повышается и возможно появление новых решений, которые не удовлетворяют исходному уравнению.

Продифференцируем три последних уравнения (1.36):

(1.44)

Сложим первые два уравнения и вычтем третье:

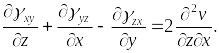
Продифференцируем это выражение по и, учитывая, что

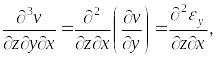
получим

(1.45)

Еще два уравнения записываются аналогично:

(1.46)

Таким образом, получена система шести дифференциальных уравнений в частных производных:

(1.47)

Уравнения (1.47) называются уравнениями неразрывности деформаций Сен-Венана.