
- •Билет№1
- •Понятие коммутации цепи. Виды коммутации.
- •2. Четырехполюсники. Понятие, классификация. Обратимость четырехполюсников.
- •Классификация четырехполюсников
- •Режим обратного питания четырехполюсников
- •Билет№2
- •1.Причины возникновения переходного процесса.
- •2.Система уравнений четырехполюсника. Понятие симметрии четырехполюсника. Основные уравнения четырехполюсников
- •3.3. Режим обратного питания четырехполюсников
- •Симметричный четырехполюсник
- •Билет№3
- •1.Составление дифференциальных уравнений цепи. Принципы решения дифференциальных уравнений. Классический метод. Классический метод расчета
- •Классический метод расчёта переходных процессов
- •2.Виды соединений нескольких четырехполюсников. Соединения четырехполюсников
- •3.13.1. Каскадное соединение
- •3.13.2. Параллельное соединение
- •3 .11.3. Последовательное соединение
- •Билет№4
- •1.Начальные условия. Законы коммутации.
- •Общая характеристика переходных процессов
- •2.Четырехполюсники в форме ||z|| параметров.
- •Билет№5
- •1.Классический метод расчета переходных процессов.
- •К лассический метод расчета
- •2.Четырехполюсники в форме ||а|| параметров. Условие его обратимости.
- •Определение а–параметров с помощью режимов короткого замыкания и холостого хода
- •Билет№6
- •1.Подключение цепи r,l к источнику энергии. Время переходного процесса.
- •2.Характеристические параметры четырехполюсника: согласованные сопротивления, мера передачи. Характеристические параметры четырехполюсника
- •Билет№7
- •1.Замыкание цепи r,l с накопленной энергией на себя. Время переходного процесса.
- •2.Четырехполюсник в форме ||а|| параметров в гиперболических функциях. Уравнения четырехполюсника в гиперболических функциях
- •Билет№8
- •1.Подключения цепи r,c к источнику энергии. Время переходного процесса.
- •2.Определение параметров эквивалентного четырехполюсника при последовательном, параллельном и каскадном соединении нескольких четырехполюсников.
- •Билет№9
- •1.Замыкание цепи r,c с накопленной энергией на себя. Время переходного процесса.
- •2.Определение параметров эквивалентного четырехполюсника при смешанном соединении нескольких четырехполюсников. . Эквивалентные схемы замещения четырехполюсника
- •Билет№10
- •1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при действительных корнях характеристического уравнения.
- •4.2.6.1. Разряд емкости на цепь rl
- •Билет№11
- •1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при комплексно-сопряженных корнях характеристического уравнения.
- •2.Вторичные параметры четырехполюсника. Примеры их нахождения. Билет№12
- •1.Подключения цепи r,l,c к источнику энергии. Время переходного процесса.
- •Переходные процессы при подключении последовательной r-l-c-цепи к источнику напряжения
- •2.Электрические фильтры понятие и классификация.
- •Билет№13
- •1.Замыкание цепи r,l,c с накопленной энергией на себя. Время переходного процесса.
- •2.Полоса пропускания и полоса задержки электрических фильтров. Граничные частоты пропускания реактивных фильтров.
2.Определение параметров эквивалентного четырехполюсника при смешанном соединении нескольких четырехполюсников. . Эквивалентные схемы замещения четырехполюсника
Л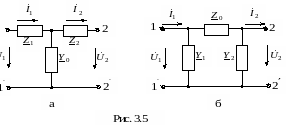 юбой
четырехполюсник можно свести к
сопротивлениям или проводимостям,
соединенным по Т– или П–образной схеме
(рис. 3.5). Эквивалентной схемой замещения
реального четырехполюсника называется
простейший трехэлементный четырехполюсник
(Т– или П–образный), имеющий такие же
юбой
четырехполюсник можно свести к
сопротивлениям или проводимостям,
соединенным по Т– или П–образной схеме
(рис. 3.5). Эквивалентной схемой замещения
реального четырехполюсника называется
простейший трехэлементный четырехполюсник
(Т– или П–образный), имеющий такие же
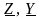 или A–параметры,
как и заданный четырехполюсник.
или A–параметры,
как и заданный четырехполюсник.
Три сопротивления Т– или П–схем должны быть рассчитаны с учетом того, что схема замещения должна обладать такими же А-параметрами, какими обладает заменяемый ей четырехполюсник.
Выразим и Т–образной схемы через , , используя уравнения, составленные по законам Кирхгофа:
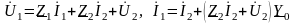 (3.18)
(3.18)
Подставляя в выражение для определения и группируя однородные члены, получим
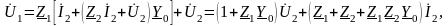
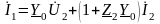 .
.
С другой стороны для данной схемы справедлива общая запись уравнений четырехполюсника в А–параметрах:
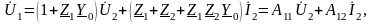
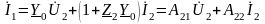 .
.
Приравняв коэффициенты при и , получим А–параметры как функции параметров Т-образной схемы замещения:
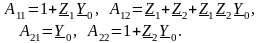 (3.19)
(3.19)
Проведя аналогичные действия, можно получить подобные соотношения для П–образной схемы четырехполюсника:
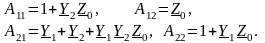 (3.20)
(3.20)
Два четырехполюсника эквивалентны, если у них равны А–параметры. Это следует из уравнений (3.9). Следовательно, если известны А–параметры какого-то четырехполюсника, то его можно заменить на эквивалентную ему Т– или П–образную схемы замещения, если определить параметры этих схем замещения в выражениях (3.19) и (3.20). При этом для Т–образной схемы замещения
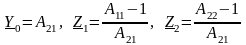 . (3.21)
. (3.21)
Параметры элементов П–образной схемы замещения
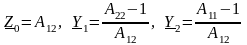 .
.
Билет№10
1.Особенности расчета переходных процессов в цепях второго порядка классическим методом при действительных корнях характеристического уравнения.
Переходные процессы в цепях второго порядка
Одна из классических задач в теории переходных процессов – анализ разряда конденсатора на цепь RL.
4.2.6.1. Разряд емкости на цепь rl
1. Независимые начальные условия для рассматриваемой цепи (рис. 4.15):
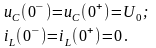
2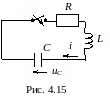 . Дифференциальное
уравнение цепи и корни характеристического
уравнения:
. Дифференциальное
уравнение цепи и корни характеристического
уравнения:
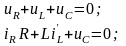
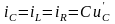 ;
;
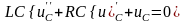 .
.
Характеристическое уравнение
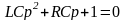 или
или
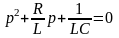 . (4.11)
. (4.11)
Корни характеристического уравнения
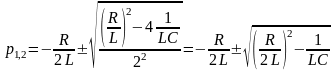 . (4.12)
. (4.12)
3. Полное
решение
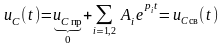 .
Вид свободной составляющей и характер
переходного процесса будут определяться
тем, какими числами будут корни
характеристического уравнения. Это
зависит от соотношения между параметрами
цепи, в частности, от подкоренного
выражения в уравнении (4.12). Здесь возможны
три варианта:
.
Вид свободной составляющей и характер
переходного процесса будут определяться
тем, какими числами будут корни
характеристического уравнения. Это
зависит от соотношения между параметрами
цепи, в частности, от подкоренного
выражения в уравнении (4.12). Здесь возможны
три варианта:
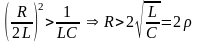 ,
где
– волновое сопротивление контура, т.е.
для низкодобротных контуров Q
< 0,5. При этом корни p1
и p2
– вещественные
отрицательные разные.
,
где
– волновое сопротивление контура, т.е.
для низкодобротных контуров Q
< 0,5. При этом корни p1
и p2
– вещественные
отрицательные разные.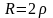 или Q
= 0,5: корни p1
= p2
– вещественные отрицательные равные
или Q
= 0,5: корни p1
= p2
– вещественные отрицательные равные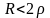 или Q
> 0,5: корни p1
и p2
– комплексные сопряженные.
или Q
> 0,5: корни p1
и p2
– комплексные сопряженные.
В первых двух случаях переходный процесс носит апериодический характер (напряжение на емкости uC монотонно затухает до нуля, не меняя своей полярности); в третьем случае процесс разряда – колебательный.
. Апериодический емкости на цепь RL
Рассмотрим
случай, когда p1,2
– действительные
и отрицательные,
т.е.
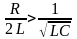 .
В этом случае переходный процесс
называется апериодическим
и вид полного решения следующий:
.
В этом случае переходный процесс
называется апериодическим
и вид полного решения следующий:
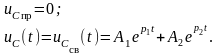
Найдем постоянные интегрирования А1 и А2:
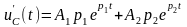 ;
;
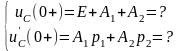
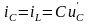
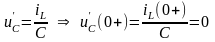
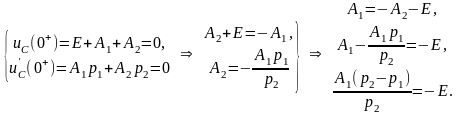
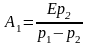 ;
аналогично:
;
аналогично:
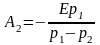 .
.
Таким образом, искомое имеет вид:
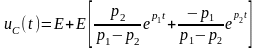 .
.
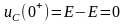 ;
;
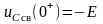 .
.
Качественно изобразим график (рис. 4.15).
Рассмотрим начальные значения:
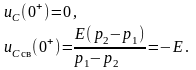
П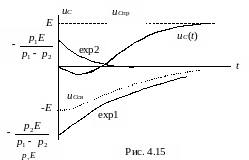 олучим
функцию изменения тока в цепи:
олучим
функцию изменения тока в цепи:
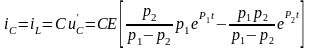 .
.
С
учетом того, что по теореме Виета
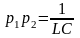 ,
,
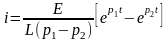 .
.
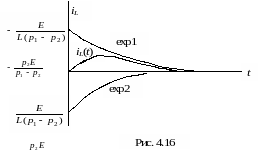
Для
построения графика (рис. 4.16) проведем
аналогичные изложенным выше исследования.
Поскольку
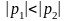 ,
первая экспонента имеет большую
постоянную времени и обращается в нуль
за больший промежуток времени. Так как
,
первая экспонента имеет большую
постоянную времени и обращается в нуль
за больший промежуток времени. Так как
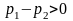 ,
,
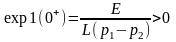 ,
,
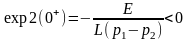 ,
тогда
,
тогда
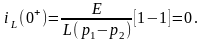
Получим функцию изменения напряжения на индуктивности
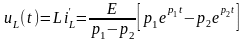 .
.
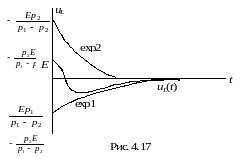
С учетом сказанного выше, exp1 находится в нижней полуплоскости и имеет большую постоянную времени, а exp2 находится в верхней полуплоскости и устремляется к нулю за меньший промежуток времени (рис. 4.17).
Начальные
условия определяются следующим образом
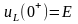 .
Поскольку
,
модули exp1, 2
отличаются
на E,
причем
exp1(0+) < exp2(0+).
.
Поскольку
,
модули exp1, 2
отличаются
на E,
причем
exp1(0+) < exp2(0+).
2.Сопротивления холостого хода и короткого замыкания четырехполюсника, их связь с характеристическими параметрами.
Нагрузочный режим четырехполюсника как результат наложения режимов холостого хода и короткого замыкания
Пусть
к выводам 2–2
четырехполюсника подключено сопротивление
нагрузки
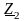 .
При этом
,
и
,
связаны соотношениями (3.9). Отсоединим
сопротивление
(режим холостого хода). Отрегулируем
входное напряжение
.
При этом
,
и
,
связаны соотношениями (3.9). Отсоединим
сопротивление
(режим холостого хода). Отрегулируем
входное напряжение
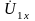 так, чтобы напряжение на выходных
разомкнутых зажимах
так, чтобы напряжение на выходных
разомкнутых зажимах
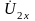 стало равным напряжению
в нагрузочном режиме:
стало равным напряжению
в нагрузочном режиме:
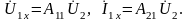
Замкнем
выводы 2–2
(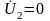 ,
режим короткого замыкания). Отрегулируем
входное напряжение
,
режим короткого замыкания). Отрегулируем
входное напряжение
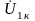 так, чтобы ток на выходных зажимах
так, чтобы ток на выходных зажимах
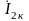 стал равным току
в нагрузочном режиме. Тогда
стал равным току
в нагрузочном режиме. Тогда
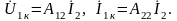
При сложении получим
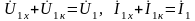 .
.
Полученные соотношения показывают, что рабочий режим четырехполюсника (нагрузка подключена к выводам 2–2) можно воспроизвести путем наложения режимов холостого хода и короткого замыкания, т.е. можно смоделировать нагрузочный режим, в некоторых случаях требующий источников большой мощности, наложением крайних нагрузочных режимов (холостого хода и короткого замыкания), когда такие источники не нужны (нагрузка не потребляет мощности!).
