14. Принцип доминирования стратегий.

Пусть имеем игру с матрицей m x n.

Каждой смешанной (в частности, чистой) стратегии 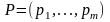игрока А поставим в соответствие строку

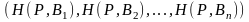(11.1)

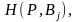
(размера 1 x n), элементами которой являются выигрыши 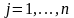, игрока А в ситуациях .

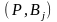В силу формулы 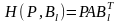строку (11.1) можно представить так:

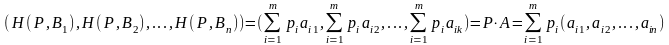(11.2)

Откуда видно, что она является выпуклой комбинацией строк матрицы А (потому что коэффициенты p неотрицательны и в сумме дают 1).

Обратно, каждой выпуклой комбинации (11.2) строк матрицы А с коэффициентами поставим в соответствие смешанную стратегию игрока А.

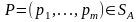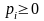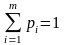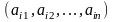Таким образом, между смешанными (в т.ч. и чистыми) стратегиями игрока А и выпуклыми комбинациями , , , , строк , матрицы А устанавливается взаимно-однозначное соответствие

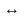(11.3)

Из (11.1) и (11.3) ясно, что каждой чистой стратегии 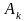, 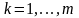игрока А ставится во взаимно-однозначное соответствие k-я строка 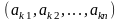матрицы А.

Если для двух выпуклых комбинаций строк матрицы А

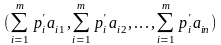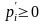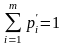, , , (11.4)

и

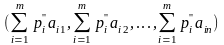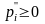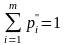, , , (11.5)

Выполняются неравенства

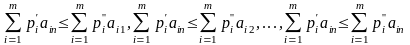(11.6)

То говорят, что строка (11.5) доминирует строку (11.4), а строка (11.4) доминируется строкой (11.5). Таким образом, строка (11.5) - доминирующая строку (11.4), а строка (11.4) - домини­руемая строкой (11.5).

Если каждое из неравенств (11.6) является равенством, то строки (11.4) и (11.5) называют дублирующими друг друга. Каж­дая из двух дублирующих строк является одновременно и доми­нируемой, и доминирующей другую.

Если каждое из неравенств (11.6) является строгим, то гово­рят, что строка (11.5) строго доминирует строку (11.4), а строка (11.4) строго доминируется строкой (11.5), или строка (11.5) является строго доминирующей строку (11.4), а строка (11.4) яв­ляется строго доминируемой строкой (11.5).

Аналогичная терминология используется и для соответст­вующих стратегий игрока А. Например, если строка (11.5) доми­нирует строку (11.4), то говорят, что стратегия Р" доминирует стратегию, Р’

Так как элементами строк, соответствующих по (11.3) сме­шанным стратегиям, являются выигрыши игрока А (см. (11.1)), то из данных определений понятно, что для игрока А дублирую­щие стратегии равнопредпочтительны, а доминируемая не дуб­лирующая стратегия заведомо для него невыгодна.

Аналогично доказывается для игрока B, только в данном случае должны выполняться неравенства

(11.12)

15. Теорема о сведении решения матричной игры к решению пары двойственных друг другу стандартных задач линейного программирования.

Сформулируем теорему, устанавливающую сведение решения любой матричной игры к решению пары двойственных задач линейного программирования специального вида, при этом будем предполагать, что все элементы матрицы игры A положительны.

. (*)

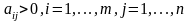Теорема: Решение матричной игры m n с матрицей A, элементы которой удовлетворяют условию (*) эквивалентно решению следующей пары двойственных друг другу стандартных задач линейного программирования.:

Найти 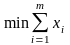при ограничениях

; (**)

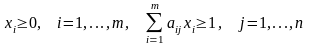Найти 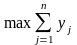при ограничениях

; (***)

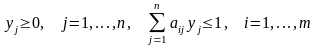Точнее говоря, если 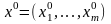- оптимальное решение задачи (**), а 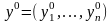- оптимальное решение задачи (***), то

Цена игры с матрицей A

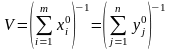
Оптимальная стратегия игрока A

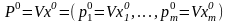
Оптимальная стратегия игрока B 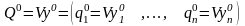И обратно.

Доказательство: