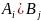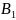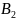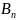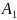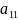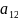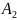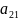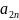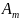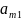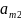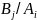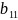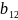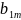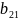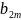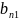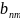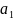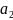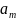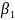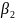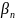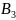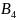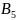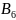- •Вопрос 2:
- •Вопрос 9.
- •Вопрос 10.
- •11. Критерий существования седловых точек
- •Вопрос 12.
- •Вопрос 13
- •14. Принцип доминирования стратегий.
- •15. Теорема о сведении решения матричной игры к решению пары двойственных друг другу стандартных задач линейного программирования.
- •16. Игры с природой. Показатель благоприятности состояния природы. Риск игрока, принимающего решение. Матрица рисков. Принятие решений в условиях риска и неопределенности.
- •17. Критерий Лапласа оптимальности чистых и смешанных стратегий относительно выигрышей.
- •Критерий (крайнего пессимизма) Вальда оптимальности чистых и смешанных стратегий.
- •Максимаксный критерий (крайнего оптимизма) оптимальности чистых и смешанных стратегий.
- •Критерий пессимизма-оптимизма Гурвица оптимальности чистых стратегий относительно выигрышей.
- •Вопрос 21

Вопрос 2:
«Основные понятия и определения теории антагонистических игр».
Ситуация называется конфликтной, если в ней участвуют стороны, интересы которых полностью или частично противоположны.
Для рационального решения задач с конфликтными ситуациями существуют научно обоснованные методы. Такие методы разработаны математической теорией конфликтных ситуаций, которая называется теорией игр.
Игра – это действительный или формальный конфликт, в котором имеется по крайней мере два участника (игрока), каждый из которых стремится к достижению собственных целей.
Игра – это математическая модель объектом, у которого есть условия:
должны существовать две противоборствующие стороны: А, В – это могут быть фирмы, люди, страны и др.
каждая из этих сторон должны иметь в своем распоряжении возможность каких-то допустимых действий
цели двух сторон должны быть противоположны (не разные, а именно противоположны – антагонисты)
каждая из противоборствующих сторон должна уметь количественно оценить результаты своих действий:
либо устроить некое отношение предпочтения (как частично упорядоченное отношение)
должны быт выигрыш функции F(a) и F(b) с числовыми значениями
каждая из сторон должна четко определить, что является ее выигрышем.
Допустимые действия каждого из игроков, направленные на достижение некоторой цели, называются правилами игры.
Игра называется парной, если в ней участвуют два игрока, и множественной, если число игроков больше двух. Далее будем рассматривать только парные игры. В такой игре участвуют два игрока - A и B, интересы которых противоположны. Под игрой (процессом игры) будет понимать ряд действий со стороны A и B.
Количественная оценка результатов игры называется платежом.
Парная игра называется игрой с нулевой суммой, или антагонистической, если сумма платежей равна нулю, т.е выигрыш одного игрока равен проигрышу другого. В этом случае для полного задания игры достаточно указать одну из величин. Если, например, a – выигрыш одного из игроков, b - выигрыш другого, то для игры с нулевой суммой b = -a, поэтому достаточно рассматривать, например, a.
Выбор и осуществление одного из действий, предусмотренных правилами, называется ходом игрока. Ходы могут быть личными и случайными.
Личный ход – это сознательный выбор игроком одного из возможных действий (например, ход в шахматной игре).
Случайный ход – это случайно выбранное действие (например, выбор карты из перетасованной колоды).
В дальнейшем мы будем рассматривать только личные ходы игроков.
Стратегией игрока называется совокупность правил, определяющих выбор его действия при каждом личном ходе в зависимости от сложившейся ситуации.
Обычно в процессе игры при каждом личном ходе игрок делает выбор в зависимости от конкретной ситуации. Однако, в принципе, возможно, что решения приняты игроком заранее (в ответ на любую сложившуюся ситуацию). Это означает, что игрок выбрал определенную стратегию, которая может быть задана в виде списка правил или программы.
Игра называется конечной, если у каждого игрока есть конечное число стратегий, и бесконечной – в противном случае.
Стратегия игрока называется оптимальной, если она обеспечивает игроку максимальный выигрыш (или, что то же самое, минимальный проигрыш), при условии, что второй игрок придерживается своей стратегии.
Если игра повторяется много раз, то игроков может интересовать не выигрыш и проигрыш в каждой конкретной партии, а средний выигрыш (проигрыш) во всех партиях.
Для того чтобы решить игру, или найти решение игры, необходимо для каждого из игроков выбрать оптимальную стратегию.
Таким образом, предмет теории игр составляют методы отыскания оптимальных стратегий игроков.
Игроки – противоборствующие модели. Если их цели противоположны, то они называются антагонистами, а игра – антагонистической.
Стратегии бывают чистые или смешанные.
Обозначим через Sac – множество чистых стратегий игрока А.
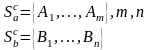 Допустим, что А и В предприняли какие-либо
ходы и сложилась ситуация (Ai, Bj) – это
есть игровая ситуация. Или (Ai, Bj) = (i,
j)
Допустим, что А и В предприняли какие-либо
ходы и сложилась ситуация (Ai, Bj) – это
есть игровая ситуация. Или (Ai, Bj) = (i,
j)
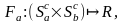
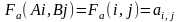
Если аij>0, то игрок А выигрывает, если равно 0 – остается изначальная ситуация.


aij=-bij
aij+bij=0 – такие игры называются с нулевой суммой выигрышей.
Поскольку каждый выигрыш определяется двойной индексацией, то выигрыш лучше всего представить в виде матрицей.
|
|
B1 |
B2 |
… |
Bn |
|
A1 |
a11 |
a12 |
|
a13 |
А= |
A2 |
a21 |
a22 |
|
a23 |
|
… |
|
|
|
|
|
Am |
a(m,1) |
a(m,2) |
|
a(m,n) |
B=-AT, в силу этого такая игра называется матричной игрой.
3. Выигрыш-функция и матрица выигрышей. Чистые стратегии игроков. Соотношение между матрицами выигрышей игроков А и В в парной антагонистической игре с нулевой суммой выигрышей.
Пусть
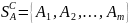 и
и
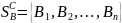 – мн-ва чистых (т.к. кажд из игр.выбирает
одну из них определенным образом)
стратегий соотв и.А и и.В. в парной
антаг.игре(с 0 суммой выйгр). m=1
проблема выбора страт.и.А отсутствует,
а n=1 пробл выб
страт. и.А тривиальна,
– мн-ва чистых (т.к. кажд из игр.выбирает
одну из них определенным образом)
стратегий соотв и.А и и.В. в парной
антаг.игре(с 0 суммой выйгр). m=1
проблема выбора страт.и.А отсутствует,
а n=1 пробл выб
страт. и.А тривиальна,
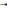 m≥2,n≥2.
m≥2,n≥2.
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
… |
… |
… |
… |
|
|
|
|
… |
|
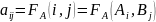 и.А в игр.ситуац
и.А в игр.ситуац
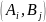 ,
i=1,2..m;
j=1,2…,n,
представляющих собой числовые знач.его
выигр-функц
,
i=1,2..m;
j=1,2…,n,
представляющих собой числовые знач.его
выигр-функц
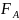 ,опред
на декартовом произв
,опред
на декартовом произв
 *
*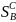 ,формируют
матрицу выигрышей и.А (платежную
матрицу(матрицу игры)).
,формируют
матрицу выигрышей и.А (платежную
матрицу(матрицу игры)).
Если и.В –противник
А и
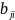 =
=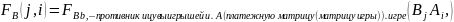 ,
i=1,2..m;
j=1,2…,n,
-выигрыш B, то матр
выигрышей В:
,
i=1,2..m;
j=1,2…,n,
-выигрыш B, то матр
выигрышей В:
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
|
… |
… |
… |
|
|
|
|
… |
|
Т.к. игра – антагонистическая,то выигр-ф-ция и.А и и.В и их матр выйгр.связаны между собой сл обр:
=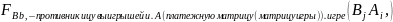 = -
= -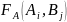 =
-
=
-
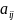 ,
(i=1,2..m;
j=1,2…,n) т.е.
,
(i=1,2..m;
j=1,2…,n) т.е.
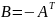 .
.
4,5 Максиминный и минимаксный принципы игроков. Показатели эффективности и неэффективности чистых стратегий игроков. Максимин и минимакс игры. Максиминные и минимаксные стратегии. Нижняя и верхняя цена игры в чистых стратегиях. Теорема о соотношениях между выигрышами и.А, показателями эффективности и неэф.стратегий,нижней и верхней ценами игры.
|
|
|
… |
|
|
|
|
… |
|
|
|
|
… |
|
… |
… |
… |
… |
|
|
|
|
… |
|
 игра с и.А и и.В,задаваемая матр выигр.А.
игра с и.А и и.В,задаваемая матр выигр.А.
Показатель
эффективности стр.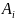 -минимальный выигрыш при этой стратегии
(мин.эл-т i-ой строки):
-минимальный выигрыш при этой стратегии
(мин.эл-т i-ой строки):
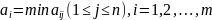
Максимином или
нижней ценой игры в чистых стратегиях
называется наибольший из показателей
эффективности стратегии
,

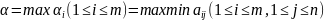
Максиминной стратегией
и.А называется стратегия
 ,
показатель эффективности которой
совпадает с максимином
,
показатель эффективности которой
совпадает с максимином
 .
Мно-во всех чистых максмин стр -
.
Мно-во всех чистых максмин стр -
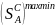 .
Принцип выбора максмин.стр в кач-ве
эффект –максиминный принцип(т.о.
при любой игре В – гарант.выигрыш ≥α)
.
Принцип выбора максмин.стр в кач-ве
эффект –максиминный принцип(т.о.
при любой игре В – гарант.выигрыш ≥α)
Показателем
неэффективности стратегии
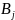 - максимальный пройгрыш и.В при этой
стр(макс.эл-т j-ого столб):
- максимальный пройгрыш и.В при этой
стр(макс.эл-т j-ого столб):
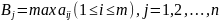
Минимакс, или верхняя
цена игры в ч. страт – наименьш из
пок-лей неэф стр
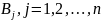 .
:
.
:
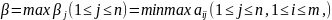
Минимаксная стр и.В
– стр
 ,
пок-тель неэф которой совпадает с
минимаксом
,
пок-тель неэф которой совпадает с
минимаксом
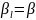 .
Мн-во всех ч.страт и.В -
.
Мн-во всех ч.страт и.В -
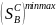 .
Принцип выбора минмакс.стр в кач-ве
эффект – минимаксный принцип(т.о.
при любой игре А не может проиграть ≥
.
Принцип выбора минмакс.стр в кач-ве
эффект – минимаксный принцип(т.о.
при любой игре А не может проиграть ≥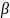 ).
).
Для нахожд ниж.и
верх.цен игры в ч.страт. дополним матр
столбцами
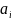 стр
,
и
стр
,
и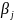 стр
стр
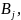
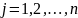 :
:
Теорема о соотнош выйг А и проиг В:
Для эл-тов матрицы
А имеют место нер-ва: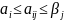 ,
,
, и, следовательно, нижняя цена
игры не больше ее верхней цены в чистых
страт:
,
,
, и, следовательно, нижняя цена
игры не больше ее верхней цены в чистых
страт:
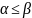 .
.
|
|
|
… |
|
|
|
|
|
… |
|
|
|
|
|
… |
|
|
… |
… |
… |
… |
|
… |
|
|
|
… |
|
|
|
|
|
… |
|
α/β |
Док-во теоремы:
По опред и имеем:
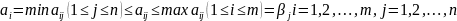 , следовательно нер-ва
,
,
доказаны.
, следовательно нер-ва
,
,
доказаны.
Т.к.
доказанное нер-во
справедливо для любых
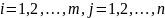 , то оно будет справ в частности для i=
, то оно будет справ в частности для i=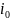 и j=
и j=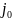 ,
соотв максимин и минимакс стр
,
соотв максимин и минимакс стр
 и
и
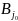 :
:
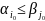
6. Устойчивые и неустойчивые игровые ситуации. Игровые ситуации, удовлетворительные для игроков, и их критерии.
Пусть имеем игру
с матр. выигр. и.А. Ситуация (
,
),
сложившаяся в рез-те выбора игроками А
и В соотв страт
и
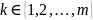 ,
,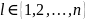 называется удовлетворительной
(приемлемой, допустимой) для и.А, если
называется удовлетворительной
(приемлемой, допустимой) для и.А, если
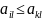 ,
i=1,2..m
, и удовлетворительной для и.В, если
,
i=1,2..m
, и удовлетворительной для и.В, если
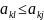 ,
,
Теорема: ситуация
(
,
),будет
удовлетворительной для и.А
т, итт,к его выигрыш
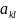 совпадает
с показателем неэф
совпадает
с показателем неэф
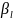 страт.
страт.
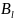 и.В
и.В
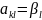 ,
т.е. будет максимальным в l-м
столбце м.А.
,
т.е. будет максимальным в l-м
столбце м.А.
Теорема: ситуация
(
,
),будет
удовлетворительной для и.В
т,итт,к его проигрыш
совпадает
с показателм эффект.
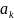 страт.
и.А.
страт.
и.А.
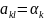 ,
те будет минимальным в k-ой
строке м.А.
,
те будет минимальным в k-ой
строке м.А.
Ситуация (
,
)
называется равновесной (устойчивой)
или седловой точной выйгрыш функции
и.А, если она удовлетворительная
для каждого из и.А и В, те:
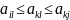 ,
i=1,2..m;
j=1,2…,n,,
или
,
i=1,2..m;
j=1,2…,n,,
или

Седловой точкой матрицы называется выигрыш , соотвеств ситуации равновесия (миним в k-ой строке и макс в l-oм столбце). Игра, матрица кот содержит хотя бы 1 такой эл-т, называется игрой с седловой тчк.
Теорема(св-во
равнозначности седл.тчк): если
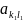 и
и
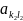 (
(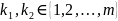 ,
,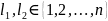 )
– седловые тчк, то
)
– седловые тчк, то
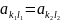 .
.
Теорема (св-во
взаимозаменяемости седловых тчк):если
и
(
,
)
– седловые тчк, то -
также селовые тчк.
-
также селовые тчк.
Стратегии
и
,
создающие равновесн ситуацию –
оптимальные.
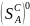 и
и
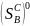 - множ-ва чист.опт страт. и.А и и.В.
- множ-ва чист.опт страт. и.А и и.В.
 - цена игры в чист.стр. Совокупность
- цена игры в чист.стр. Совокупность
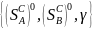 и множ-в
и
чист.опт.стр
- полное (общее) решение игры в
чист.страт. А
и множ-в
и
чист.опт.стр
- полное (общее) решение игры в
чист.страт. А
 какой-л
пары чист.опт.стр
какой-л
пары чист.опт.стр
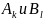 и цены игры в ч.опт.стр называется частным
решением игры в чистых стратегиях.
и цены игры в ч.опт.стр называется частным
решением игры в чистых стратегиях.
Теорема(критерий существования цены игры в чистых стр): для существования цены игры в чистых страт. необх и достат существование у матр этой игры седловой тчкю.
Теорема: в игре
с седловой тчк множ-во чист.опт.страт
и.А совпадает с множ-вом его максиминных
стратегий:
=
,
а множ-во чист.отпт.страт и.В совп с
множ-вом его минимаксн страт:
=
.
В игре без седловой тчк ни у одного из
игроков нет опт страт:
=
= Ø, хотя максиминные стратегии и.А и
минимаксные и.В всегда сущ:
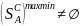 ,
,
 .
.
7. Равновесная ситуация. Седловая точка выигрыш-функции и седловая точка матрицы игры. Свойства равнозначности и взаимозаменяемости седловых точек.
Ситуация (
,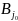 )
называется равновесной (устойчивой)
или седловой точкой выйгрыш функции
и.А, если она удовлетворительная
для каждого из и.А и В, те:
)
называется равновесной (устойчивой)
или седловой точкой выйгрыш функции
и.А, если она удовлетворительная
для каждого из и.А и В, те:
 ,
i=1,2..m;
j=1,2…,n,,
или
,
i=1,2..m;
j=1,2…,n,,
или
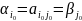
Седловой точкой
матрицы называется выигрыш
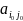 ,
соотвеств ситуации равновесия (миним
в
-ой
строке и макс в
-oм
столбце). Игра, матрица кот содержит
хотя бы 1 такой эл-т, называется игрой
с седловой тчк.
,
соотвеств ситуации равновесия (миним
в
-ой
строке и макс в
-oм
столбце). Игра, матрица кот содержит
хотя бы 1 такой эл-т, называется игрой
с седловой тчк.
Теорема(св-во
равнозначности седл.тчк): если
 и
и
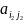 (
( ,
,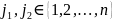 )
– седловые тчк, то
)
– седловые тчк, то .
.
Доказательство:
т.к.
–
седловая точка, то по правому неравенству
(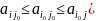 при
при
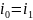 ,
,
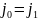 ,
,
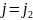 ,имеем
,имеем
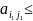
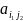 ,
а т.к.
,
а т.к.
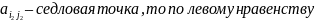 (
,
при
(
,
при
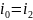 ,
,
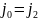 ,
,
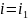 ,
получим
,
получим
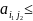 .
из данных нерав-в следует нер-во:
.
применив аналогич.рассужд снач к седловой
тчк
,
затем к
,
получим:
.
из данных нерав-в следует нер-во:
.
применив аналогич.рассужд снач к седловой
тчк
,
затем к
,
получим:
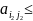 .
.
Теорема (св-во
взаимозаменяемости седловых тчк):если
и
(
,
)–
седловые тчк, то
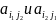 -
также селовые тчк.
-
также селовые тчк.
Доказательство:
т.к.
и
-
седл точки,то по по св-ву равнозначности
седл.тчк. справедливо
,
из которого получаем
 .
С др стороны, по опред.пок-теля эффект
и пок-ля неэф будем иметь:
.
С др стороны, по опред.пок-теля эффект
и пок-ля неэф будем иметь:
 .
Из рав-ва (
.
Из рав-ва (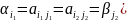 следует, что
следует, что
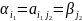 ,
а это означает, что
–
седл тчк. Аналогично с
,
а это означает, что
–
седл тчк. Аналогично с
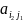 .
.
|
|
|
|
|
|
|
|
|
2 |
|
2 |
|
2 |
4 |
2 |
|
|
|
0 |
|
1 |
1 |
0 |
|
2 |
6 |
2 |
3 |
2 |
7 |
2 |
|
0 |
5 |
1 |
7 |
1 |
4 |
0 |
|
|
|
2 |
|
2 |
7 |
2/2 |
8. Цена игры в чистых стратегиях. Стратегии оптимальные во множестве чистых стратегий. Полное (общее) и частно решение игры в чистых стратегиях. Критерий существования цены игры в чистых стратегиях. Соотношения между множествами оптимальных и максиминных (минимаксных) стр.
Стратегии и , создающие равновесн ситуацию – оптимальные. и - множ-ва чист.опт страт. и.А и и.В.
- цена игры в чист.стр. Совокупность
и множ-в
и
чист.опт.стр
- полное (общее) решение игры в
чист.страт. А
какой-л
пары чист.опт.стр
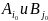 и цены игры в ч.опт.стр называется частным
решением игры в чистых стратегиях.
и цены игры в ч.опт.стр называется частным
решением игры в чистых стратегиях.
Теорема(критерий существования цены игры в чистых стр): для существования цены игры в чистых страт. необх и достат существование у матр этой игры седловой тчк.
Доказательство:
необходимость. Пусть сущ.цена
игры в чистых страт, т.е. нижняя цена
игры α совпадает с верхней
.
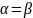
Пусть
- максимин.стр и.А, а
-минимаксн.стр.и.В.
тогда
 ,
,
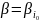 .
Рассмотрим
,стоящий
на пересеч
-той
строки и
-столбца.
Из предыдущ рав-в, опред показ эфф и
неэф:
.
Рассмотрим
,стоящий
на пересеч
-той
строки и
-столбца.
Из предыдущ рав-в, опред показ эфф и
неэф:
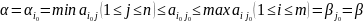 ,
отсюда в силу рав-ва
,
отсюда в силу рав-ва
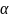 и
,
получим:
,
кот означ, что
явл седл тчк. Необходимость доказана.
и
,
получим:
,
кот означ, что
явл седл тчк. Необходимость доказана.
Достаточноть.
Пусть сущ седл тчк.
,
тогда :
.
Отсюда по опред нижн и верхн цен игры:
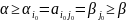 ,
т.е.
,
т.е.
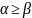 .
Но по теореме (
,
,
)
и поэтому
,
существует цена игры в чистых страт.
.
Но по теореме (
,
,
)
и поэтому
,
существует цена игры в чистых страт.
Теорема: в игре
с седловой тчк множ-во чист.опт.страт
и.А совпадает с множ-вом его максиминных
стратегий:
=
,
а множ-во чист.отпт.страт и.В совп с
множ-вом его минимаксн страт:
=
.
В игре без седловой тчк ни у одного из
игроков нет опт страт:
=
= Ø, хотя максиминные стратегии и.А и
минимаксные и.В всегда сущ:
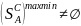 ,
.
,
.
Доказательтсво:
пусть
и
-
опт стр. и.А и и.В. Тогда по опр опт стр
-
седл.тчк. Но тогда справедливо нер-во
,
установленное в доказательстве
достаточности. Из него и нер-ва
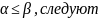 два
нер-ва
и
два
нер-ва
и
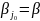 ,
первое из кот означ,что стр
-
максиминная, а второе,что
-минимаксная.
,
первое из кот означ,что стр
-
максиминная, а второе,что
-минимаксная.
Что в игре без седловых тчк ни одна из максиминных и минимаксн стр не явл оптимальной, поск в этой игре вообще нет оптимальных страт – очевидно.
Пусть
-
седл.тчк. ,
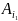 -
максиминная стр и.А,
-
максиминная стр и.А,
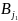 -минимаксная
и.В. Из максиминности
по
опред следует, что
-минимаксная
и.В. Из максиминности
по
опред следует, что
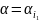 ,
а из минимаксности
,
что
,
а из минимаксности
,
что
 ,
тогда
,
тогда
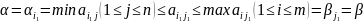 .
Но т.к. сущ седл тчк
,
то по теореме существования цены игры
в чистых страт. имеет место нерав-во
,
с учетом которого из
получаем
.
Но т.к. сущ седл тчк
,
то по теореме существования цены игры
в чистых страт. имеет место нерав-во
,
с учетом которого из
получаем
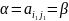 .
А это означает, что
- седл тчк. и,следовательно, стр
и
-
оптмальные.
.
А это означает, что
- седл тчк. и,следовательно, стр
и
-
оптмальные.