Вопрос 12.

Цена игры в смешанных стратегиях. Стратегии, оптимальные во множестве смешанных стратегий. Полное (общее) и частное решения игры в смешанных стратегиях. Основная теорема теории игр Дж. фон Неймана.

Если нижняя и верхняя цены игры в смешанных стратегиях совпадают, то их общее значение V= = называется ценой игры в смешанных стратегиях. Нижняя и верхняя цены игры в чистых стратегиях α и β и цены игры в смешанных стратегиях V связаны между собой неравенствами α≤V≤β.

Стратегии P^O и Q^O соответственно игроков А и В, удовлетворяющие равенствам V=α(P^O)=β(Q^O) (и тогда это общее значение очевидно равно H(P^O,Q^O)), называется оптимальными смешанными стратегиями игроков А и В.

Таким образом, оптимальные смешанные (в частности, чистые) стратегии P^O и Q^O соответственно игроков А и В обладают тем свойством, что если один из игроков придерживается своей оптимальной стратегии, то противнику невыгодно отклоняться от своей оптимальной стратегии.

Множество оптимальных смешанных стратегий соответственно игроков А и В обозначим через (S_A)^О и (S_B)^О.

Полным решением игры в смешанных стратегиях называется трехэлементная совокупность {(S_A)^O,(S_B)^O,V}. Любая пара оптимальных стратегий P^O и Q^O соответственно игроков А и В и цена игры в смешанных стратегиях V образуют частное решение в смешанных стратегиях.

Основная теорема теории игр Дж. фон Неймана:

Любая матричная игра имеет решение в смешанных стратегиях, т.е. существует цена игры в смешанных стратегиях V и оптимальные смешанные стратегии P^O и Q^O соответственно игроков А и В, т.е.

V= =

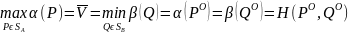
Вопрос 13

Критерии оптимальных смешанных стратегий в терминах данной цены игры, выигрыш-функции и множеств смешанных стратегий игроков.

Теорема. (Критерии оптимальных стратегий).

Пусть V-цена игры, H(P,Q) – выигрыш-функция, S_A и S_B – множества смешанных стратегий соответственно игроков А и В.

1. Для того чтобы стратегия Р^О игрока А была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство:

H(P^О,Q)≥V

Для любого Q ϵ S_B , т.е. выбор игроком А оптимальной стратегии Р^О гарантирует ему выигрыш H(P^О,Q), не меньший цены игры V, при любой стратегии Q игрока В.

2. Для того чтобы стратегия Q^O игрока В была оптимальной, необходимо и достаточно, чтобы выполнялось неравенство

H(P^О,Q)≤V

Для любого Р ϵ S_А , т.е. выбор игроком В оптимальной стратегии Q^О гарантирует ему проигрыш H(P,Q^О), не больший цены игры V, при любой стратегии Р игрока А.

Данная теорема остаётся справедливой, если в её формулировке множество смешанных стратегий S_A и S_B заменить соответственно на множество чистых стратегий S^С_A и S^С_B.

Доказательство:

Утверждение 1:

Необходимость:

Пусть Р⁰ – оптимальная стратегия игрока А. тогда по теореме фон Неймана показатель эффективности 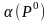стратегии Р⁰ равен цене игры V:

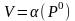(1)

Рассматривая как показатель эффективности 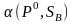стратегии Р⁰ относительно множества S_B смешанных стратегий игрока В, будем иметь по определению:

(2)

Из равенств (1) и (2) получаем неравенство H(P^О,Q)≥V

Достаточность:

Пусть для некоторой стратегии Р0 игрока А выполняется неравенство H(P^О,Q)≥V. Для доказательство оптимальности стратегии Р0 достаточность показать справедливость равенства

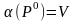
Так как неравенство выполняется для любой стратегии 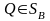игрока В, то

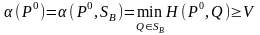(3)

Но цена игры V равна нижней цене игры V, по определению которой

(4)

Совокупность (3) и (4) эквивалентна равенству . Достаточность доказана

Утверждение 2:

АНАЛОГИЧНЫЕ РАССЖУДЕНИЯ.