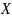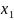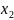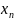10. Математическое ожидание. Определение мат. Ожидания. Свойства мат. Ожидания. Вычисление мат. Ожидания биноминального распределения , распределения Пуассона и геометрического распределения.

Математическим ожиданием дискретной случайной величины называется сумма произведений возможных значений случайной величины на их вероятности, то есть, если X - дискретная случайная величина, закон распределения которой имеет вид:

находится по формуле: .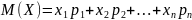

Отметим, что при большом числе опытов среднее арифметическое наблюдавшихся

значений случайной величины приближается к ее математическому ожиданию.

Замечание. Математическое ожидание случайной величины есть величина

неслучайная.

Основные свойства математического ожидания:

1.Математическое ожидание постоянной величины равно постоянной, т.е., если

С = const, то M(С) = М

2. Постоянный множитель можно выносить за знак математического ожидания, т.е M(CX)= CM(X).

3. Математическое ожидание суммы двух случайных величин равно сумме математических ожиданий этих величин, т.е. M(X+Y) = M(X) +M (Y)

4. Математическое ожидание произведения двух независимых случайных величин равно произведению их математических ожиданий, т.е. M(XY) = M(X) M(Y), где X и Y- независимые случайные величины.

5.Если производится n независимых испытаний, в каждом из которых вероятность появления события А постоянна и равна р. Тогда математическое ожидание М(Х) числа появления события А в n независимых испытаниях

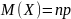
Распределения Пуассона

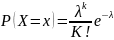
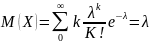
11. Дисперсия и средне квадратичное отклонение . Определение дисперсии. Свойства дисперсии. Вычисление дисперсии для известных дискретных случайных величин.

Пусть X – случайная величина. Случайную величину 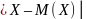называют

отклонением. Очевидно, что математическое ожидание отклонения равно 0:

M [X – M(X)] = 0

Дисперсией (рассеянием) случайной величины называют математическое ожидание квадрата отклонения от ее математического ожидания, т.е. 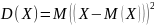. (1)

Дисперсия характеризует меру рассеяния возможных значений случайной величины по отношению к ее математическому ожиданию.

Нередко вместо формулы (1) в вычислениях используют эквивалентную ей формулу 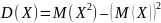(2)

Свойства дисперсии:

1. Дисперсия постоянной величины равна нулю, т.е. D(С) =0

2. Постоянный множитель можно выносить за знак дисперсии, возводя его в квадрат, т.е. .

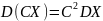3. Дисперсия суммы или разности двух независимых случайных величин равна сумме их дисперсий D(X ± Y) = D(X) ± D(Y),

4. Дисперсия числа появления события А в n независимых испытаниях, в каждом из которых вероятность события А постоянна, равна произведению числа испытаний на вероятности появления и непоявления события в одном испытании: D(X) = npq.

Следствие: D(C + X) = D(X), где С – постоянная.

12.Определение непрерывной случайной величины и её плотности. Свойства функции распределения: вероятность попадания в интервал, монотонность, ограниченность, пределы на бесконечности, непрерывность слева. Свойства плотности.

Непрерывной называют случайную величину, которая может принимать любые значения из некоторого заданного интервала, например, время ожидания транспорта, температура воздуха в каком-либо месяце, отклонение фактического размера детали от номинального, и т.д. Интервал, на котором она задана, может быть бесконечным в одну или обе стороны.

Плотность вероятности непрерывной случайной величины, она же дифференциальная функция распределения вероятностей - аналог закона распределения дискретной с.в. Но если закон распределения дискретной с.в. графически изображается в виде точек, соединённых для наглядности ломаной линией (многоугольник распределения), то плотность вероятностей графически представляет собой непрерывную гладкую линию (или кусочно-гладкую, если на разных отрезках задаётся разными функциями). Аналитически задаётся формулой. Если закон распределения дискретной с.в. ставит каждому значению x в соответствие определённую вероятность, то про плотность распределения такого сказать нельзя. Для непрерывных с.в. можно найти только вероятность попадания в какой-либо интервал. Считается, что для каждого отдельного (одиночного) значения непрерывной с.в. вероятность равна нулю. И графически вероятность попадания в интервал выражается площадью фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом. Свойства плотности вероятности: 1) Значения функции неотрицательны, т.е. f(x)≥0 2) Основное свойство плотности вероятности: несобственный интеграл от плотности вероятности в пределах от -∞ до +∞ равен единице (геометрически это выражается тем, что площадь фигуры, ограниченной сверху графиком плотности вероятности, снизу - осью OX, равна 1).

Функция распределения случайной величины, она же интегральная функция распределения вероятностей - это функция, определяющая для каждого значения x вероятность того, что случайная величина (ξ) примет значение меньшее, чем x: F(x) = P(ξ < x). Численно функция распределения равна площади фигуры, ограниченной сверху графиком плотности вероятности, снизу осью ОХ, с боков - рассматриваемым интервалом. Основные свойства: 1) Значения функции распределения лежат в интервале [0; 1], т.е. 0 ≤ F(X) ≤ 1 2) Это функция неубывающая, при x→-∞ F(X)→0, при x→+∞ F(X)→1 3) Вероятность попадания в интервал (a, b) определяется формулой F(b) - F(a) Взаимосвязь интегральной и дифференциальной функций распределения вероятностей: