1. Изображение Лапласа, оригинал, ограничения на оригинал, показатель роста. Аналитичность изображения. Теорема единственности.

Функция называется оригиналом, если она удовлетворяет следующим условиям: 1) при . 2) - кусочно-непрерывная при . 3)Существуют такие числа M>0 и что для всех t выполняется неравенство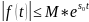 т.е. при возрастании t функция может возрастать не быстрее некоторой показательной функции . показатель роста

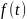
Изображением Лапласа называется комплексного переменно определяемая интегралом

Для всякого оригинала изображение 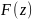существует в полуплоскости где – показатель роста функции , причем функция является аналитической в этой полуплоскости .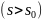

Если функция F(p) служит изображением двух оригиналов и , то эти оригиналы совпадают друг с другом во всех точках в которых они непрерывны.

2. Функция Хевисайда, её изображение. Теорема подобия. Свойство линейности оператора Лапласа. Смещение изображения. Теорема запаздывания.

Функция Хевисайда — специальная математическая функция, чьё значение равно нулю для отрицательных аргументов и единице для положительных аргументов:

Если т.е. умножение аргумента оригинала на положительное число приводит к делению изображения и его аргумента на это число.

Линейной комбинации оригиналов соответствует такая же линейная комбинация изображений, т.е. если и 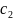- постоянные числа, то

Если , то т.е. умножение оригинала на функцию влечет за собой смещение переменной z.

Если , , то , то т.е. запаздывание оригинала на положительную величину приводит к умножению оригинала без запаздывания на

3. Дифференцирование изображения. Дифференцирование оригинала. Таблица изображений основных функций.

Если 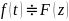, то

Если и функции являются оригиналами, то

4. Приложения операционного исчисления к решению дифференциальных уравнений и систем дифференциальных уравнений.

Метод решения обыкновенных линейных дифференциальных уравнений с постоянными коэффициентами п-го порядка состоит в том, что, используя свойства линейности преобразования Лапласа, теорему единственности и теорему дифференцирования оригинала, от дифференциального уравнения переходим к алгебраическому уравнению относительно соответствующих изображений, которое называется операторным (операционным). Находя решение операторного уравнения, а затем его оригинал, тем самым находим решение задачи Коши для линейного дифференциального уравнения п-го порядка.

Таким образом, решение задачи Коши осуществляется по следующей схеме: Дифференциальное уравнение:

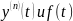, с начальными условиями: в предположении, что - оригиналы (задача Коши)

Lap - преобразование Изображающее алгебраическое (операторное) уравнение Решение операторного уравнения - преобразование Решение задачи Коши

Для восстановления оригинала по его изображению могут быть использованы свойства преобразования Лапласа (L-преобразования) и таблицы изображений.

5. Свёртка функций, перестановочность свертки. Изображение свертки.

Свёрткой функций называют функцию этот интеграл не меняет своего значения от перестановки функций , поэтому свёртка двух функций симметрична относительно свертываемых функций. Изображение свертки двух оригиналов равно произведению их изображений если 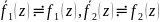то:

6. Интегрирование оригинала. Интегрирование изображения, следствие о вычислении интеграла : .

Если 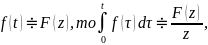т.е. интегрированию оригинала от 0 до t соответствует деление его изображения на z.

Если т.е. интегрированию изображения от p до соответствует деление его оригинала на t.

Если и также является оригиналом, то

7. Приложения операционного исчисления к решению интегральных уравнений. Вычисление интегралов с помощью операционного исчисления.

Метод перехода к изображающему уравнению позволяет легко найти решение интеграла вида

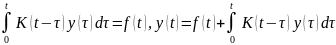
В которых функции являются оригиналами, поскольку входящий в эти уравнения интеграл представляет собой свёртку функций .

1.Пространство событий. Случайное, достоверное, невозможные события. Сумма и произведение событий. Несовместимые события. Полная группа событий. Противоположное событие. Свойства алгебры событий.

Случайным событием называют событие которое происходит с некоторой вероятностью в пространстве событий( ). Событие называется достоверным, если оно происходит всегда. Событие называется невозможным, если оно никогда не происходит. Сложением событий называют событие, которое происходит, если произойдет либо одно, либо другое из складываемых событий. Умножением событий называют событие, которое произойдет, только если произойдут все перемножаемые события. События несовместимы, если одновременно они произойти не могут. События образуют полную группу если сумма их вероятностей равна достоверному событию. Противоположным событием называют событие, которое отражает вероятность того, что событие не произошло.

1. (A + B)C = AC + DC.

2. AB + C = (A + C)(B + C).

3. A + B = A · B.

4. A · B = A + B

2. Классическая схема вероятностного пространства . Элементарное событие. Равновозможность(равновероятность) событий. Описание классической схемы вероятностного пространства и классического определения вероятности.

Фундаментальные свойства вероятности (В1, В2, В3) Простейшие следствия фундаментальных свойств: 1) вероятность невозможного события, 2) вероятность противоположного события, 3) ограниченность значения вероятности, 4) монотонность,5) аддитивность.

Событие называется элементарным, если оно не разлагается в сумму событий вероятность которых отличается от невозможного события.

Несколько событий A1, A2, . . . , An называются равновозможными, если

в силу симметрии условий опыта относительно этих событий вероятности их

одинаковы. Таким образом, классическая схема есть сумма вероятностей случайных, равновероятных и невозможных событий.

1. ; 2) ; 3) ; 4) Если А принадлежит В и они относятся к одному пространству то ; 5) .

3. Геометрические вероятности. Описание «геометрического» вероятностного пространства. Определение геометрической вероятности. Геометрическая вероятность удовлетворяет фундаментальным свойствам.

Чтобы преодолеть недостаток классического определения вероятности, состоящий в том, что оно неприменимо к испытаниям с бесконечным числом исходов, вводят геометрические вероятности — вероятности попадания точки в область (отрезок, часть плоскости и т. д.).

Пусть отрезок l составляет часть отрезка L(который является здесь вероятностным пространством, в качестве вероятностного пространства могут быть использованы также и двумерный и трехмерные координаты). На отрезок L наудачу поставлена точка. Это означает выполнение следующих предположений: поставленная точка может оказаться в любой точке отрезка L, вероятность попадания точки на отрезок l пропорциональна длине этого отрезка и не зависит от его расположения относительно отрезка L. В этих предположениях вероятность попадания точки на отрезок l определяется равенством

Р = Длина l / Длина L.

4. Аксиоматическое построение теории вероятностей. Пространство элементарных событий, сигма-алгебра событий, вероятность. Вероятностное пространство. Теорема сложения вероятностей. Следствие: оценка сверху вероятности нескольких событий.

U – Пространство элементарных событий и вместе с тем произвольное множество. Что позволяет проводить такие операции: 1) 2) ; 3) U|A (Дополнение).

Пусть U — множество элементов , которые называются элементарными событиями, а   — множество подмножеств U, называемых случайными событиями (или просто — событиями), а U — пространством элементарных событий.

• Аксиома I (алгебра событий).   является алгеброй событий.

• Аксиома II (существование вероятности событий). Каждому событию   из   поставлено в соответствие неотрицательное действительное число  , которое называется вероятностью события  .

• Аксиома III (нормировка вероятности). P(U)=1.

• Аксиома IV (аддитивность вероятности). Если события A и B не пересекаются, то P(A+B)=P(A)+P(B);

• Совокупность объектов  , удовлетворяющая аксиомам I—IV, называется вероятностным пространством. 

Если семейство попарно несовместимых событий, то

5. Условная вероятность. Теорема об условном вероятностном пространстве относительного события, имеющего ненулевую вероятность. Определение условной вероятности . Теорема произведения . Независимая пара событий. Теорема умножения независимых событий. Вероятность появления хотя бы одного события. Формула полной вероятности и формулы Бейеса. Независимые испытания. Схема независимых испытаний. Схема Бернулли. Вероятность появления события m раз.

Условной вероятностью события   при условии, что произошло событие  , называется число

Условная вероятность определена только в случае, когда  .

Пусть A - произвольное событие, а события B₁, B₂, …, B_n - попарно несовместны и образуют полную группу событий, т.е.  . Тогда имеет место следующая формула для вероятности события A - формула полной вероятности -

Если событие A произошло, то вероятность того, что имело место событие B_k

вычисляется по формуле Байеса: 

Пусть проводится серия из n испытаний, в результате каждого из которых событие А может произойти или не произойти. Предполагаем, что вероятность p наступления события А в каждом испытании постоянна, т.е. не зависит ни от номера испытания, ни от результатов предыдущих испытаний.

Последовательность испытаний, удовлетворяющих указанному условию, называется последовательностью независимых испытаний (или схемой Бернулли).

Таким образом, в схеме Бернулли для каждого испытания имеется лишь два исхода:

1) событие А, P(A) = p; 2) событие A , P( A ) = q = 1 - p.

Вероятность Pn(k) того, что в серии из n испытаний в схеме Бернулли событие А наступит ровно k раз (безразлично, в какой последовательности), выражается формулой Бернулли

6.Случайные величины. Примеры случайных величин. Определение случайной величины и функции её распределения.

Случайной величиной называется величина, которая в результате испытания

приобретает то или иное числовое значение из некоторого множества. При этом заранее неизвестно, какое значение имела случайная величина примет в результате опыта.

Случайная величина называется дискретной, если все ее возможные значения

изолированы друг от друга и их можно занумеровать.

Случайную величину называют непрерывной, если она может принимать любые значения из некоторого промежутка (конечного или бесконечного).

Законом распределения случайной величины называется соответствие между ее возможными значениями и вероятностями, с которыми эти значения принимаются.