6. Степенные ряды (по степеням (z – a)). Теорема Абеля. Радиус сходимости и круг сходимости. Аналитичность суммы степенного ряда.

Естественным обобщением многочленов являются функции, заданные в виде суммы ряда по степеням z — z_o:

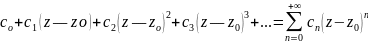(8)

Теорема 8.1 (Абеля). Если ряд (8) сходится при некотором значении z*, то он абсолютно сходится при любом 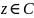таком, чт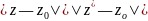о . Если же ряд (8) расходится при при некотором z**, то он рас­ходится и при любом комплексном z таком, что 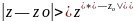. Существует неотрицательное действительное число R, называемое радиусом сходимости, такое, что ряд сходится абсолютно при 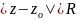и расходится при 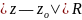. Круг 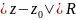называется кругом сходимости. Обозначим через S(z) сумму ряда (8) в круге сходимости.

Теорема 8.2. Функция S(z) аналитична в круге сходимости и

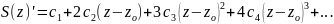(9)

При этом ряд в правой части (9) имеет тот же радиус сходимости, что и ряд (8).

7. Производная функции комплексного переменного, аналитичность в точке и области. Геометрический смысл производной, сохранение углов. Свойства производных.

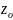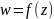Определение 6.1. Пусть функция f (z) определена в окрестности точки . Производная функции комплексного переменного в точке определяется в точности также как и для функции действительного переменного: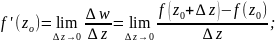

Функция комплексного переменного называется аналитической на открытой области G, если она имеет производную в каждой точке этой области и производная непрерывна. Аналитичность в точке означает существование и непрерывность производной в некоторой окрестности этой точки. Аналитичность на замкнутой области D означает суще­ствование и непрерывность производной на некоторой открытой области G, содержащей D.

8. Производная функции zⁿ . Определение e^z , sin(z) , cos(z) , tg (z), их разложение в степенные ряды и производные. Гиперболические функции sh(z) , ch(z) , th(z) , основное гиперболическое тождество, формулы сложения, производные, разложения в степенные ряды, связь с тригонометрическими функциями. .

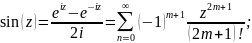
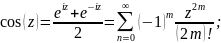
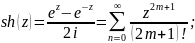
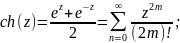
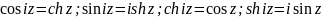
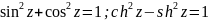
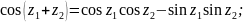
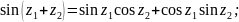
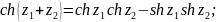
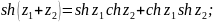
Производные для функций комплексного переменного не отличаются от производных функций действительного переменного

9. Условия Коши-Римана, критерий аналитичности.

Теорема 6.3 (условия Коши-Римана). Функция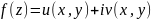 аналитична в точке тогда и только тогда, когда в неко­торой окрестности этой точки существуют и непрерывны частные производные 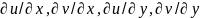и выполнены условия Коши-Римана

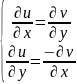
10. Обратные функции. Понятие многозначной функции. Многозначные функции Ln(z) и корень n-ой степени.

Многозначная функция (многолистная) комплексного переменного это правило, в силу которого каждому z из области определения D ставится в соответствие несколько (возможно бесконечное число) значений w.

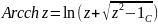
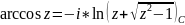
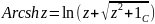
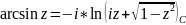
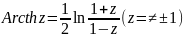
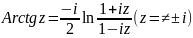
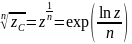
11. Кривые на комплексной плоскости, непрерывные, замкнутые, гладкие, кусочно-гладкие. Интеграл от функции компл. переменного, его свойства и сведение к криволинейному интегралу. Свойства интеграла (линейность, аддитивность, оценка).

Определение 14.1. Путем или кривой L на комплексной плоскости называется отображение 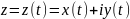отрезка действительной прямой 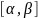в комплексную плоскость C. Точка 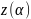называется нача­лом пути L, а точка 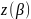- его конец. Путь L называется замкнутым, если начало совпадает с концом. Образ отображения 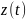, т. е. множество 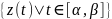называется носителем кривой L.

Кривая L называется непрерывной, если функци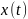и и 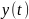, а тем самым и функция непрерывны. Путь L называется гладким, если су­ществует, непрерывна и отлична от нуля производная 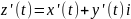в любой точке 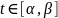; для замкнутого пути дополнительно требует­ся, что бы односторонние производные 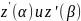совпадали. Путь L называется кусочно гладким, если существует разбиение 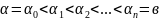отрезка такое, что на каждом отрезке 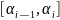путь L гладок.

Определение 14.5. Интегралом функции по кривой L называется

предел интегральных сумм, если параметр разбиения стремится к 0:

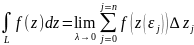
Сформулируем без доказательства стандартные свойства интеграла

Свойство 14.6 (линейность). Для любых 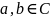и любых функций 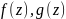интегрируемых по кривой L имеет место равенство:

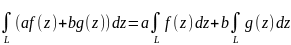
Свойство 14.7 (аддитивность). Если функция интегрируема по сумме кривых 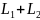, то она интегрируема по каждой кривой и

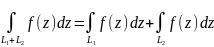
Свойство 14.8 (изменение знака). Если функция интегрируема по кривой L, то

Свойство 14.10 (оценка интеграла). Пусть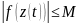 для лю­бого спрямляемой кривой L. Тогда

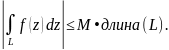
Если учесть, что 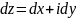и

,

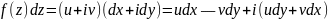то формула сведения интеграла функции к криволинейным инте­гралам получается такой:

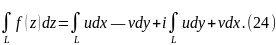
В частности, из этой формулы вытекает, что если кривая L кусочно-гладкая, а кусочно-непрерывна, то интеграл 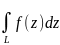существует.