Граничные условия для векторов магнитного поля. Условия для нормальных составляющих векторов в и н. Билет 20

Граничные условия для касательных составляющих векторов магнитного поля. Поверхностный ток.

0 Применим к контуру первое уравнение Максвелла в интегральной форме: (1). Левую часть представим в виде суммы интегралов по участкам контура:

(2)

на участках АВ и СD может быть представлен:

Устремим h0 так, чтобы участки контура находились в разных средах. Тангенциальная составляющая распределена равномерно.

Так как векторы в 1 и 2 средах, а также вектор имеют конечную величину, то

В результате предельного перехода, примененного к соотношению (2), получим

(3)

. Пусть на границе раздела сред S имеются поверхностные токи.

1. В этом случае правую часть соотношения (3) можно преобразовать

С учетом приведенных соотношений, предельный переход, выполненный в соотношении (3) приведет к следующему соотношению:

(5)

Билет 21 Полная система граничных условий.

Граничные условия на поверхности идеального проводника

Полная (обобщенная) система граничных условий

(1)

Отсутствующие граничные условия являются следствием приведенных, при использовании материальных уравнений

Для переменного электромагнитного поля .

2 Уравнение Максвелла: , где .

Это получится, если .

на поверхности идеального проводника тангенциальная составляющая и нормальная обращаются в нуль.

Билет 22

Баланс энергий электромагнитного поля

качественное уравнение

(1)

; ; (2)

уравнение баланса имеет следующий вид:

(12)

Билет 23

Плотность энергии электромагнитного поля

запас электромагнитного поля в объеме V: (1)

Так как энергии представлены в виде интегралов по объему, то подынтегральные выражения можно трактовать как объемную плотность энергий, а их сумму — как объемную плотность энергии электромагнитного поля.

; (3) (4)

Пусть в объеме V существует независимо два электромагнитных поля. Энергия суммарного электромагнитного поля:

(5)

Билет 24 Скорость распространения энергии электромагнитных волн

В пространстве, в котором распространяется электромагнитная энергия, выделим энергетическую трубку (некий протяжный объем, на боковой поверхности которого вектор Пойнтинга равен нулю).

Пусть, за время t через боковую поверхность S прошла энергия W и оказалась сосредоточенной между сечениями S и S₁ , между которыми, расстояние l. Направление единичного вектора совпадает с направлением распространения энергии.

Тогда скорость распространения энергии:

(1)

Энергию, заключенную между торцами S и S₁:

(2),

где w — объемная плотность энергии, а S^’ — среднее сечение.

Если промежуток t взять достаточно малым, чтобы не успел измениться, то энергию:

(3)

Приравняем (2) к (3) и выразим 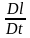. Получим:

(4)

Найдем предел от соотношения (4) при t0. Получим:

(5)

Получили общее выражение для величины скорости распространения энергии. Если предположить, что векторы и , а стало быть, и неизменны в пределах поперечного сечения цилиндра, то в этом случае, векторы и совпадают по направлению распространения энергии.

(6)