
- •1.2. Представление технических объектов как объектов управления
- •1.3. Принципы управления
- •1.3.1. Принцип разомкнутого управления
- •1.3.2. Принцип компенсации
- •1.3.3. Принцип обратной связи
- •1.3.4. Комбинированный принцип управления
- •1.4. Функциональные схемы систем автоматического управления
- •1.5. Классификация систем автоматического управления Классификация систем автоматического регулирования по характеру изменения задающего воздействия
- •Классификация систем автоматического управления в зависимости от числа управляемых переменных
- •Классификация систем автоматического управления по остальным признакам
- •2. Математическое описание линейных систем автоматического управления
- •2.1. Статические и динамические характеристики систем автоматического управления
- •2.2. Преобразование Лапласа
- •2.2.1. Основные свойства преобразования Лапласа
- •2.3. Передаточные функции
- •2.4. Решение дифференциальных уравнений операторным методом
- •2.5. Структурные схемы систем автоматического управления
- •2.6. Передаточные функции систем автоматического регулирования
- •3. Временные и частотные характеристики систем автоматического управления и ее элементов
- •3.1. Временные характеристики
- •3.2. Частотные характеристики
- •3.4. Типовые динамические звенья
- •3.5. Уравнения и характеристики типовых динамических звеньев
- •1. Дифференциальное уравнение
- •2. Передаточная функция
- •3.6. Интегро-дифференцирующие звенья
- •4. Устойчивость линейных систем автоматического управления
- •4.1. Понятие устойчивости системы
- •4.2. Алгебраические критерии устойчивости
- •4.2.1. Критерий Гурвица
- •4.2.2. Критерий Рауса
- •4.3. Частотные критерии устойчивости
- •4.3.1. Критерий Михайлова
- •4.3.2 Критерий Найквиста
- •4.4. Оценка устойчивости сар по логарифмическим частотным характеристикам
- •4.5. Запасы устойчивости систем автоматического регулирования
- •4.6. Выделение областей устойчивости
- •4.6.1. Сущность метода d – разбиения
3. Временные и частотные характеристики систем автоматического управления и ее элементов
3.1. Временные характеристики
Дифференциальные уравнения являются исчерпывающим математическим описанием САУ. Решения дифференциальных уравнений показывают изменения параметров объекта управления во времени. Однако, на практике получение решений дифференциальных уравнений является не простой задачей. Но, несмотря на это, решения дифференциальных уравнений широко используются как при анализе, так и при синтезе систем. Только для этого рассматриваются решения дифференциальных уравнений при некоторых стандартных (типовых) воздействиях.
Временными характеристиками называются графики решений дифференциальных уравнений при типовых входных воздействиях. В качестве типовых входных воздействий в основном рассматриваются:
- единичное ступенчатое воздействие (единичная ступенчатая функция) 1(t);
- единичное импульсное воздействие (t).
Единичное ступенчатое воздействие – это функция
![]() ,
(3.1)
,
(3.1)
график которой приведен на рис.3.1.
Переходной
функцией h(t)
называется переходный процесс, вызванный
единичным ступенчатым воздействием
1(t)
при нулевых начальных условиях, т.е.
h(t)
характеризует реакцию системы на
единичное ступенчатое воздействие, что
отражено на рис. 3.2. Если амплитуда
ступенчатого воздействия отлична от
1, т.е.
![]() ,
где с
– константа, то реакция системы на
выходе определяется соотношением:
,
где с
– константа, то реакция системы на
выходе определяется соотношением:
![]() .
(3.2)
.
(3.2)
Физическая интерпретация 1(t) – резкое изменение (скачком) входного воздействия.
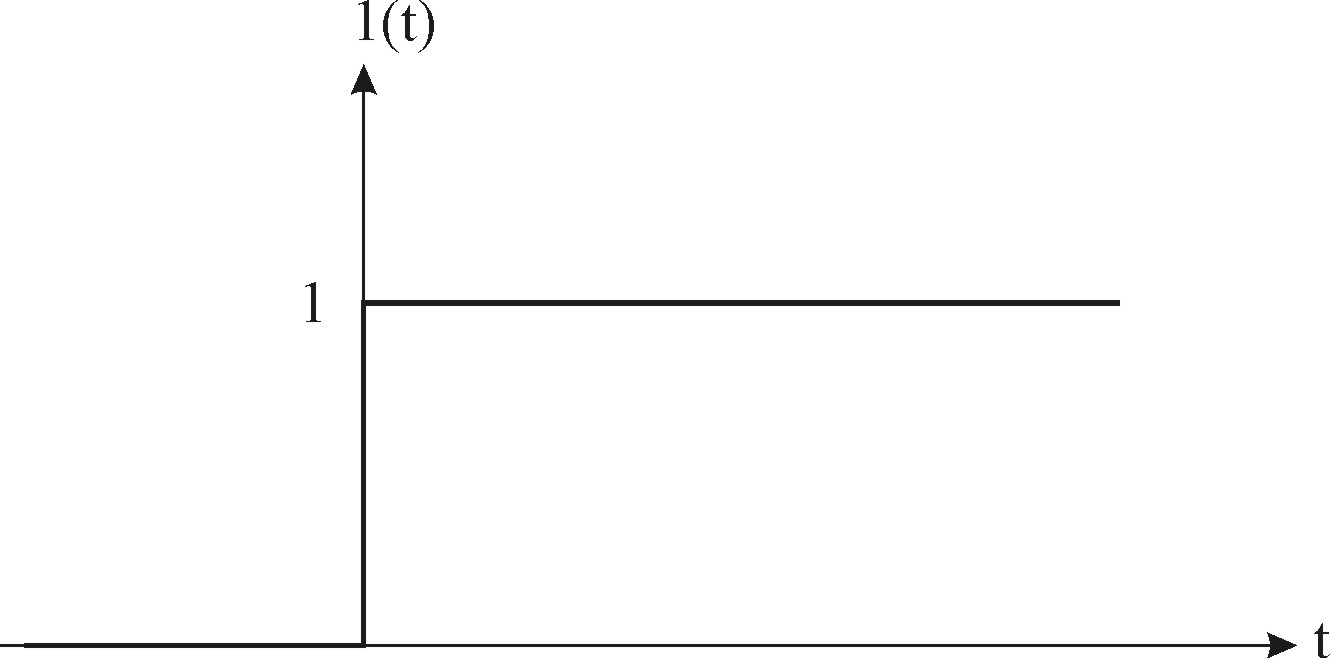
Рис. 3.1. Единичное ступенчатое воздействие
.
![]()
Рис. 3.2. Реакция системы на единичное ступенчатое воздействие
Единичным импульсным воздействием (единичной импульсной функцией) (t) называется дельта – функцией Дирака, представляющая собой импульс бесконечно большой амплитуды и бесконечно малой длительности:
![]() ,
(3.3)
,
(3.3)
площадь которого равна 1, т.е.
![]() .
(3.4)
.
(3.4)
График (t) представлен на рис. 3.3.
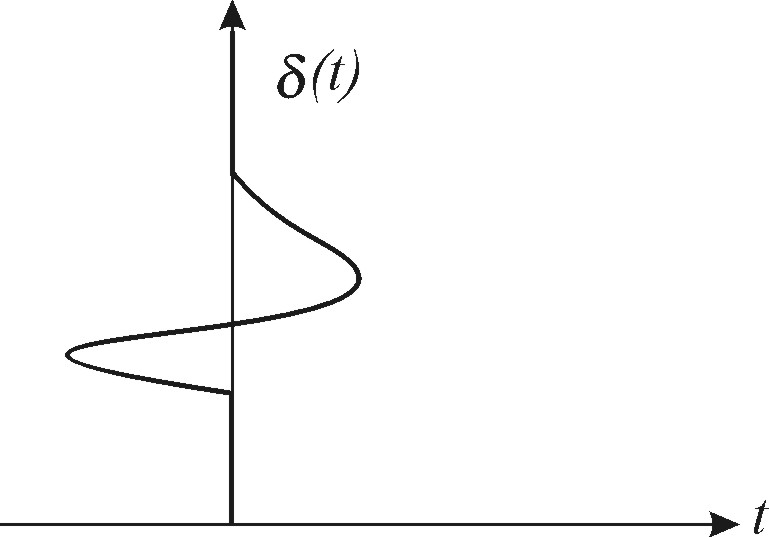
Рис. 3.3. Единичное импульсное воздействие
Импульсной переходной (весовой) функцией (t) называется переходный процесс, вызванный единичным импульсным воздействием (t) при нулевых начальных условиях, т.е. (t) характеризует реакцию системы на входные воздействия типа - функции, что отражено на рис. 3.4.
![]()
Рис. 3.4. . Реакция системы на единичное импульсное воздействие
Физическая интерпретация (t) – удар.
Единичное линейное воздействие – это линейная функция с единичным наклоном под углом 450 к оси времени, представленная на рис. 3.5 и определяемая выражением
![]() .
(3.5)
.
(3.5)
Функцией x(t) называется переходный процесс, вызванный единичным линейным воздействием при нулевых начальных условиях, т.е. x(t) характеризует реакцию системы на линейное входное воздействие q(t) , что отражено на рис. 3.6.
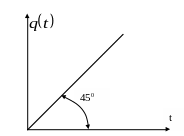
Рис. 3.5 Единичное линейное воздействие.
Если наклон прямой к оси времени отличен от 450, т.е. k≠1, то реакция системы на выходе определяется соотношением
![]() .
(3.6)
.
(3.6)

Рис. 3.6. Реакция на единичные линейные воздействия
Физическая интерпретация q(t) это изменение входного воздействия с постоянной скоростью, что характерно для систем управлениz приводами подачи станков с ЧПУ при обработке прямолинейных поверхностей.
Между типовыми входными воздействиями имеется следующая связь:
![]() ;
(3.7)
;
(3.7)
![]() .
(3.8)
.
(3.8)
Аналогична связь между реакциями системы на типовые входные воздействия, а именно:
![]() ;
(3.9)
;
(3.9)
![]() .
(3.10)
.
(3.10)
Рассмотрим связь между передаточной функцией W(p) и функциями w(t), h(t) и x(t).
Так как
![]() ,
(3.11)
,
(3.11)
то изображение весовой функции равно передаточной функции:
ω(p)=W(p). (3.12)
Аналогично можно записать: так как
![]() ,
(3.13)
,
(3.13)
то изображение переходной функции
![]() .
(3.14)
.
(3.14)
Откуда имеем, что
![]() .
(3.15)
.
(3.15)
Так как
![]() ,
(3.16)
,
(3.16)
то изображение функции x(t)
![]() , (3.17)
, (3.17)
т.е.
![]() (3.18)
(3.18)
Таким
образом: весовая функция
![]() является оригиналом передаточной
функции
является оригиналом передаточной
функции
![]() ;
переходная функция
;
переходная функция
![]() оригиналом
оригиналом
![]() ;
а
;
а
![]() - оригиналом
- оригиналом
![]() .
.
Заключение.
Типовые воздействия
![]() и
и
![]() с одной стороны описывают поведение
системы в экстремальных (тяжелых)
условиях, а с другой стороны существенно
упрощают возможности получения
математической модели системы (объекта,
элемента).
с одной стороны описывают поведение
системы в экстремальных (тяжелых)
условиях, а с другой стороны существенно
упрощают возможности получения
математической модели системы (объекта,
элемента).
