- •Вопрос 1: Производная функции, ее геометрический и механический смысл.
- •Вопрос 2: Производная суммы, произведения и частного.
- •Вопрос 3: Производная сложной функции.
- •Вопрос 4: Производная обратной функции.
- •Вопрос 5: Производные высших порядков.
- •Вопрос 6: Теоремы Ролля, Лагранжа, Коши, их применение.
- •Вопрос 7: Правило Лопиталя.
- •Вопрос 8: Условия монотонности функции. Экстремумы функции.
- •Вопрос 9: Отыскание наибольшего и наименьшего значений непрерывной на отрезке функции.
- •Вопрос 10: Исследование функций на выпуклость, вогнутость. Точки перегиба.
- •Вопрос 11: Асимптоты кривых. Общая схема построения функций.
- •Вопрос 12: Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования.
- •Вопрос 13 : Непосредственное интегрирование. Интегрирование по частям и подстановкой.
- •Вопрос 14: Интегрирование рациональных функций путем разложения на простейшие дроби.
- •Вопрос 15: Интегрирование выражений, содержащих тригонометрические функции.
- •Вопрос 16: Интегрирование некоторых иррациональных выражений.
- •Вопрос 17: Определенный интеграл как предел интегральных сумм. Основные свойства определенного интеграла.
- •Вопрос 18: Формула Ньютона-Лейбница.
- •Вопрос 19:Вычисление определенного интеграла: интегрирование по частям.
- •Вопрос 20: Приложение интегралов к вычислению площадей плоских фигур.
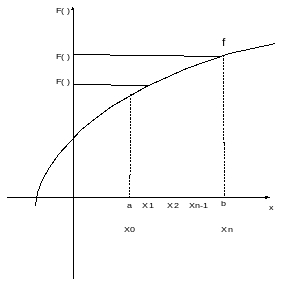
Вопрос 17: Определенный интеграл как предел интегральных сумм. Основные свойства определенного интеграла.
Рассмотрим непрерывную положит. на [a,b] функцию n.
Организуем производное разбиение отрезка ab на n-произвольных частей
a=x0 <x1<x2…<xn-1
Длину каждого участка разбиения [xk-1 , xk]
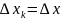 – ранг разбиения
– ранг разбиенияНа каждом участке
 выберем точку
выберем точку
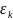 и в каждой точке
найдем значение функции f(
).
и в каждой точке
найдем значение функции f(
).Составим выражение
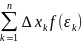 ,
называемое интегральной суммой.
,
называемое интегральной суммой.Если предел интегральной суммы не зависит от способа разбиения и выбора точки оси координат, то он называется определенным интегралом(при условии существования)
Свойства:
Интеграл от суммы равен сумме интегралов
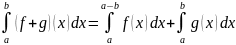 .
Доказательство этого свойства с помощью
определенного либо:
.
Доказательство этого свойства с помощью
определенного либо:

Формула интегрирования по частям:
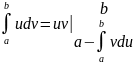
a<c<b
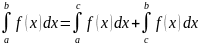
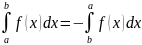
Интегралы на симметричном отрезке [-a; a] F(x) – нечетное
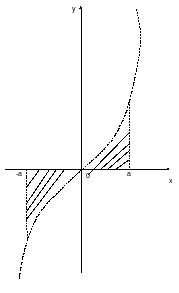
Вопрос 18: Формула Ньютона-Лейбница.
Формула Ньютона-Лейбница - даёт соотношение между операциями взятия определенного интеграла и вычисления первообразной. Формула Ньютона-Лейбница - основная формула интегрального исчисления.
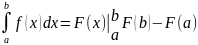
Данная формула верна для любой функции f(x), непрерывной на отрезке [а, b], F - первообразная для f(x). Таким образом, для вычисления определенного интеграла нужно найти какую-либо первообразную F функции f(x) , вычислить ее значения в точках a и b и найти разность F(b) – F(a).
Вопрос 19:Вычисление определенного интеграла: интегрирование по частям.
Определенным
интегралом от функции f
на [a, b]
обозначается
 – это предел интегральной суммы
независящей от способа разбиения и
выбора точки
при условии, что ранг разбиения стремится
к нулю.
– это предел интегральной суммы
независящей от способа разбиения и
выбора точки
при условии, что ранг разбиения стремится
к нулю.
Решается определенный интеграл с помощью формулы Ньютона-Лейбница:
Этапы решения определенного интеграла следующие:
1) Сначала находим первообразную функцию (неопределенный интеграл).
2)
Подставляем значение верхнего предела
в первообразную функцию:
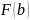
3)
Подставляем значение нижнего предела
в первообразную функцию:
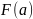
4)
Рассчитываем разность, то есть находим
число.
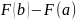
Формула интегрирования по частям:
Вопрос 20: Приложение интегралов к вычислению площадей плоских фигур.
Площадь фигуры, ограниченной графиками функции
У1
= f1(x)
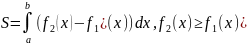
У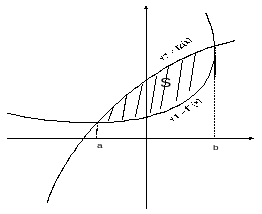 2
= f2(x)
a,b
– точки пересечения графика функции.
2
= f2(x)
a,b
– точки пересечения графика функции.
Объем тела полученного вращением вокруг оси ОХ криволинейной трапеции которая ограничена графиком функции у = f(x) и прямыми x=a, x=b

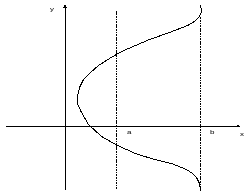
Если интеграл берется от функции в пределах, т.е. на [a, b]
Интегрирование имеет разрыв, то интеграл называется несобственным интегралом 2-го рода.
Вопрос 21: Несобственные интегралы.
Если интеграл функции содержит в качестве одного или нескольких пределов интегралов он называется несобственным интегралом 1-го рода.
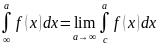
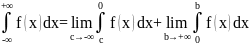
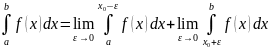
Если указанные пределы при вычислении несобственного интеграла существуют и конечны, интеграл называется сходящимся, в противном случае расходящимся.
Вопрос 22: Функции нескольких переменных. Область определения.
Z = z(x1, x2 … x n): D принадлежит Rn -> R
z(x, y) = x2 + y2
Пример:
Изобразить область определения функции
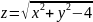
D (z) = x2 + y2 – 4 >=0
x2 + y2 >=4
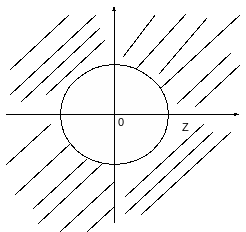
D(z) = {(x, y); x, y принадлежит R
x2 + y2 >=0}
Линией уровня 2-ух переменных z=f(x,y) при пересечении графиков этой функции плоскости параллельна плоскости Oxy, т.е. кривая z=c
Вопрос 23: Частные производные.
Пусть дана функция z = f(x,y) которая определена в иск. окрестности точки z по переменной x, называется её обычная производная взятая при фиксированном y.
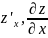
Аналогично
определяется частная производная
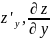
Z= x2 + xy + exy + 1
Z’x = 2x + y + exy z’y = x + xexy
Z = x2y
Z’ x ( y – число) = 3yx2
Z’ y ( x – число) = x3
Z = ln(xy)
Z’ x = 1/xy * y = 1/x
Z’y = 1/xy * x = 1/y
Вопрос 24: Градиент.
Рассмотрим функцию 2-ух переменных z = f(xy) которая дифференцируема в некоторой точке m(x0y0).
Градиентом функции z называется вектор координаты которого совпадают со значением частных производных этой функции в точке m.
Формула:
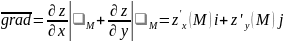
Градиент показывает направление самого быстрого изменения функции.
Вопрос 25: Частные производные высших порядков.
Определим частные производные 2-го порядка:
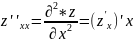
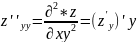
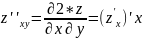 -
смешанная производная 2-го порядка
-
смешанная производная 2-го порядка
Z’’yx = (Z’y)’x - смешанная производная 2-го порядка
Теорема: Смешанные производные равны. Т.е. Z’’ xy = Z’’ yx
Вопрос 26: Экстремум функции двух переменных.
Локальные экстремумы ФНП:
Пусть функция z=f(x, y) определяется в некоторой окрестности f(z) имеет точку f0 – локальный max, если для любой точки xy из указанной окрестности z(x0y0) > z(x, y), аналогично тип функции z.
Теорема:
Если f(z) = f(xy) имеет в точке n0(x0, y0) локальный экстремум, т.е. max или min имеет частные производные 1-го порядка, то все эти частные производные точки m0 = 0, также точки называются стационарными.
Алгоритм исследования ФНП на экстремумы:
Определить область определения.
Найти главные производные 1-го порядка.
Решить систему z’ x= 0
z’ y= 0, M(xk, yk)
Найти частную производную 2-го порядка
A = z’’ xx
B = z’’ yy
C = z’’ xy
В каждой точке Mk (xk, yk) находим значение определителя по формуле
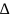 (Mk)
= AB
– C2
если
<
0, то в точке Mk
нет экстремума, если
>
0, то
(Mk)
= AB
– C2
если
<
0, то в точке Mk
нет экстремума, если
>
0, то
в точке Mk есть экстремум: при < 0 A>0 (C>0) минимум
при > 0 A<0 (C<0) минимум
= 0, нужны дополнительные исследования
|
x y |
X Y
|
Xx xy Xy yy |
Найти значение экстремума
f max z max