
- •Вопрос 1: Производная функции, ее геометрический и механический смысл.
- •Вопрос 2: Производная суммы, произведения и частного.
- •Вопрос 3: Производная сложной функции.
- •Вопрос 4: Производная обратной функции.
- •Вопрос 5: Производные высших порядков.
- •Вопрос 6: Теоремы Ролля, Лагранжа, Коши, их применение.
- •Вопрос 7: Правило Лопиталя.
- •Вопрос 8: Условия монотонности функции. Экстремумы функции.
- •Вопрос 9: Отыскание наибольшего и наименьшего значений непрерывной на отрезке функции.
- •Вопрос 10: Исследование функций на выпуклость, вогнутость. Точки перегиба.
- •Вопрос 11: Асимптоты кривых. Общая схема построения функций.
- •Вопрос 12: Первообразная. Неопределенный интеграл, его свойства. Таблица основных формул интегрирования.
- •Вопрос 13 : Непосредственное интегрирование. Интегрирование по частям и подстановкой.
- •Вопрос 14: Интегрирование рациональных функций путем разложения на простейшие дроби.
- •Вопрос 15: Интегрирование выражений, содержащих тригонометрические функции.
- •Вопрос 16: Интегрирование некоторых иррациональных выражений.
- •Вопрос 17: Определенный интеграл как предел интегральных сумм. Основные свойства определенного интеграла.
- •Вопрос 18: Формула Ньютона-Лейбница.
- •Вопрос 19:Вычисление определенного интеграла: интегрирование по частям.
- •Вопрос 20: Приложение интегралов к вычислению площадей плоских фигур.
Вопрос 6: Теоремы Ролля, Лагранжа, Коши, их применение.
Теорема Ролля:
Если функция определена на отрезке [a, b] и непрерывна на нём, дифференцируема на (a, b) и принимает равные значения на концах отрезка, то существует точка с из (a, b) в которой производная равна нулю.
Основные пункты.
а) Функция определена на [a, b]
б) Дифференцируема на (a, b)
в) f(a) = f(b)
г)
f (c)
= 0
(c)
= 0

Теорема Лагранжа:
Если
функция непрерывна на [a,
b]
дифференцируема на (a,
b),
то существует точка с из (a,
b)
такая, что выполнено равенство такая,
что выполнено равенство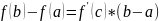 - Формула конечных разностей. Геометрически
теорема Лагранжа означает, что найдётся
такая точка c,
где касательная параллельна секущей.
- Формула конечных разностей. Геометрически
теорема Лагранжа означает, что найдётся
такая точка c,
где касательная параллельна секущей.
Теорема Коши:
Пусть
даны две функции ![]() и
и ![]() такие,
что:
такие,
что:
и определены и непрерывны на отрезке
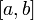 ;
;производные
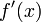 и
и 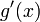 конечны
на интервале
конечны
на интервале 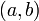 ;
;производные и не обращаются в нуль одновременно на интервале
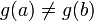 ;
;
тогда
![]() ,
где
,
где ![]()
(Если
убрать условие 4, то необходимо усилить
условие 3: g'(x) не должна обращаться в
нуль нигде в интервале ![]() .)
.)
Геометрически
это можно переформулировать так:
если
и ![]() задают
закон движения на плоскости (то есть
определяют абсциссу и ординату через
параметр
задают
закон движения на плоскости (то есть
определяют абсциссу и ординату через
параметр ![]() ),
то на любом отрезке такой кривой, заданном
параметрами
),
то на любом отрезке такой кривой, заданном
параметрами ![]() и
и ![]() ,
найдётся касательный вектор, коллинеарный вектору
перемещения от
,
найдётся касательный вектор, коллинеарный вектору
перемещения от ![]() до
до ![]() .
.
Вопрос 7: Правило Лопиталя.
Метод
нахождения пределов функций, раскрывающий
неопределённости вида
![]() и
и
![]() .
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен пределу отношения
их производных.
.
Обосновывающая метод теорема утверждает,
что при некоторых условиях предел
отношения функций равен пределу отношения
их производных.
Условия:
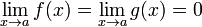 или
или 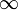 ;
;и дифференцируемы в проколотой окрестности ;
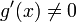 в
проколотой окрестности
;
в
проколотой окрестности
;существует
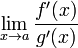 ,
тогда существует
,
тогда существует 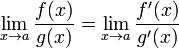 .
.
Пределы также могут быть односторонними.
Вопрос 8: Условия монотонности функции. Экстремумы функции.
Условия монотонности функции
Пусть
функция ![]() непрерывна
на
непрерывна
на ![]() и
имеет в каждой
и
имеет в каждой
точке ![]() производную
производную ![]() Тогда
Тогда
возрастает
на
тогда
и только тогда, когда ![]()
убывает
на
тогда
и только тогда, когда ![]()
Пусть функция непрерывна на и имеет в каждой точке производную Тогда
если ![]() то
строго
возрастает на
то
строго
возрастает на ![]()
если ![]() то
строго
убывает на
то
строго
убывает на ![]()
Обратное,
вообще говоря, неверно. Производная
строго монотонной функции может
обращаться в ноль.
Однако, множество точек, где производная
не равна нулю, должно быть плотно на
интервале
Пусть ![]() и
всюду на интервале определена
производная
Тогда
строго
возрастает на интервале
тогда
и только тогда, когда выполнены следующие
два условия:
и
всюду на интервале определена
производная
Тогда
строго
возрастает на интервале
тогда
и только тогда, когда выполнены следующие
два условия:
![]()
Аналогично, строго убывает на интервале тогда и только тогда, когда выполнены следующие два условия:
![]()
![]()
Экстремум функции – максимальное или минимальное значение функции на заданном множестве. Точка, в которой достигается экстремум, называется точкой экстремума. Соответственно, если достигается минимум — точка экстремума называется точкой минимума, а если максимум — точкой максимума. В математическом анализе выделяют также понятие локальный экстремум (соответственно минимум или максимум). Алгоритм нахождения 1) D(f); 2) 3) =0 или не существует; 4) Нанести критические точки на действительную ось и определить знак функции на каждом отрезке.
