Вопрос 13 : Непосредственное интегрирование. Интегрирование по частям и подстановкой.

Непосредственное (табличное) интегрирование - метод интегрирования, при котором интеграл путем тождественных преобразований подынтегральной функции (или выражения) и применения свойств интеграла приводится к одному или нескольким табличным интегралам.

Метод интегрирования по частям: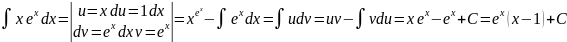

Интегрирование подстановкой (замена переменной): Если функция  f ( z ) определена и имеет первообразную при  z   Z ,  а функция z = g ( x ) имеет непрерывную производную при  x   X  и её область значений  g ( X )   Z , то функция  F ( x ) =  f  [ g ( x )]  g' ( x ) имеет первообразную на  Х  и

 F ( x ) dx =   f [ g ( x )] • g' ( x ) dx =   f ( z ) dz .

Вопрос 14: Интегрирование рациональных функций путем разложения на простейшие дроби.

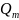Выражение вида: , где и 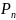– многочлены степени m и n.Если m<n дробь правильная, если m n – неправильная.

При вычислении интегралов вида: 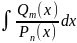требуется выделить целую часть (деление многочлена на многочлен или выражением числителя через знаменатель)

А)

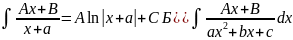
Б1: метод внесения под знак дифференциала Б2: выделение полного квадрата в знаменателе, представление числителя как дифференциал знаменателя, разложение на 2 интеграла.

(*)

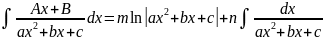
Где m и n можно найти продифференцировав обе части неравенства (*) и приравняв соответствующие коэффициенты при степенях x, второй интеграл находится выделением полного квадрата в знаменателе.

В) 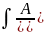n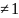

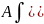
Г) Интегралы вида: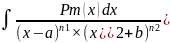 - В этом случае когда знаменатель дроби представлен в виде произведения неразложимых далее сомножителей, в этом случае, подъинтегральную дробь нужно представить в виде суммы простейших дробей со знаменателем x-a будет равно n1 штук причем в каждой следующей дроби показатель степени увеличивается на 1 в числителе должен стоять многочлен в общем виде степени на 1 меньше чем знаменатель. .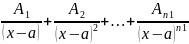

Далее приводим все дроби к общему знаменателю и приравниваем коэф. при соответствующих степенях находим Ai, Bi, Ci

Вопрос 15: Интегрирование выражений, содержащих тригонометрические функции.

Рассмотрим интеграл вида:

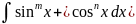
Возможен следующий случай:

1. m и n – четные, тогда воспользуемся формулами понижения порядка:

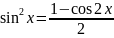
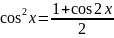
2. хотя бы одно из m и n нечетное(пусть m – нечетное)

а)«метод отщипления»

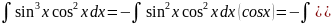
б)домножение на функцию которая стоит в нечетной степени:

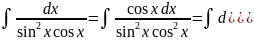
3. Интегралы вида:

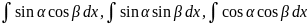
Вычисляются с помощью: ; ;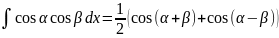

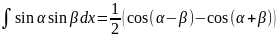
4. Интегралы вида: 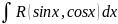, где R- производная функция, т.е. выполнено

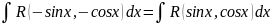, то применяется подстановка t=tgx =>

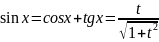
Вопрос 16: Интегрирование некоторых иррациональных выражений.

Интегралы вида:

1)

a)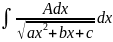 - выделение полного квадрата в знаменателе использование формул 5, 6

б)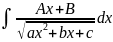 – внесение под знак дифференциала, разложение на суммы 2-ух интегралов и выделение полного квадрата в знаменателе.

2) 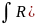– решается заменой подкоренного выражения

=>

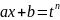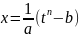
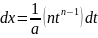
Если в подъинтегральном выражении содержится несколько корней разных степеней то за новую переменную t нужно взять корень степени k из подкоренного выражения, где k – наименьшее общее выражение всех показателей корней входящих в подъинтегральную функцию т.е.:

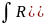
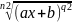) dx

ax+b = 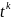k=НОК(n₁;n₂)

2)

Интегрирование с помощью тригонометрических подстановок:

А)

Замена: