17. Отношение эквивалентности
Отношение
эквивалентности
(
)
на множестве X —
это бинарное
отношение, для которого выполнены
следующие условия:
Рефлексивность:
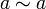для
любого a в X,Симметричность: если
,
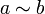то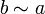 
,Транзитивность: если и
,
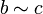то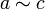 
.
Запись вида « » читается как «a эквивалентно b».
Связанные определения
Классом эквивалентности C(a) элемента a называется подмножество элементов, эквивалентных a. Из вышеприведённого определения немедленно следует, что, если
,
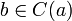то C(a)
= C(b).
Множество всех классов эквивалентности обозначается X / ˜.
Для класса эквивалентности элемента a используются следующие обозначения: [a], a / ˜,
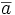.Множество классов эквивалентности по отношению является разбиением множества.
Примеры отношений эквивалентности
Равенство («
»),
тривиальное отношение эквивалентности
на любом множестве, в частности, вещественных
чисел.Сравнение по модулю, («а ≡ b (mod n)»).
В Евклидовой геометрии
Отношение конгруэнтности («
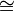»).Отношение подобия («
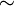»).Отношение параллельности прямых («
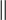»).Эквивалентность функций в математическом анализе:
Говорят,
что функция 
эквивалентна
функции 
при 
,
если она допускает представление
вида 
,
где 
при
.
В этом случае пишут 
,
напоминая при необходимости, что речь
идет о сравнении функций при
.
Если 
при 
,
эквивалентность функций
и
при
,
очевидно, равносильна соотношению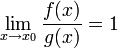 
.
18. Свойства счетных множеств.
Множество, эквивалентное множеству натуральных чисел, называется счётным. Т.е. множество счётно, если его можно пронумеровать.
Множество
целых чисел эквивалентно множеству
натуральных чисел. Следовательно
множество целых чисел счётно:
; 
бесконечное
множество может быть эквивалентно
своему подмножеству.
Любое бесконечное подмножество счётного множества также счётно. Иными словами: не существует мощности, промежуточной между мощностью счётных множеств и мощностями конечных. Счётность - это минимально возможная мощность бесконечных множеств.
В теории
множеств счётное
мно́жество есть бесконечное
множество,
элементы которого возможно
пронумеровать натуральными
числами.
Более формально: множество X является
счётным, если существует биекция 
,
где 
обозначает
множество всех натуральных чисел.
Другими словами, счётное множество —
это множество, равномощное множеству
натуральных чисел.
Свойства
Любое подмножество счётного множества не более чем счётно (т.е. конечно или счётно).[1]
Объединение конечного или счётного числа счётных множеств счётно.[1]
Прямое произведение конечного числа счётных множеств счётно.
Множество всех конечных подмножеств счётного множества счётно.
Множество всех подмножеств счётного множества континуально и, в частности, не является счётным.
19 Свойства отношений
В математике бинарным отношением называется подмножество декартова произведения двух множеств. В частности, бинарным отношением на множестве называется множество упорядоченных парэлементов этого множества.
Свойства отношений
Бинарные отношения могут обладать различными свойствами, такими как
Рефлексивность:
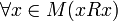.Антирефлексивность (иррефлексивность):
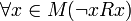.Симметричность:
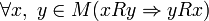.Антисимметричность:
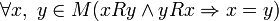.Транзитивность:
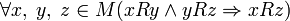.Связность:
.Асимметричность:
.
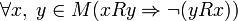Асимметричность эквивалентна
одновременной антирефлексивности и
антисимметричности отношения.
Виды отношений
Рефлексивное транзитивное отношение называется отношением квазипорядка.
Рефлексивное симметричное транзитивное отношение называется отношением эквивалентности.
Рефлексивное антисимметричное транзитивное отношение называется отношением (частичного) порядка.
Антирефлексивное антисимметричное транзитивное отношение называется отношением строгого порядка.
Полное антисимметричное транзитивное отношение называется отношением линейного порядка.
Антирефлексивное асимметричное отношение называется отношением доминирования.
20. Бесконечные множества. Счетные множества. Множества делятся на конечные и бесконечные. Конечное множество — множество, количество элементов которого конечно, то есть, существует неотрицательное целое число k, равное количеству элементов этого множества. В противном случае множество называется бесконечным. Бесконечные множества в свою очередь делятся на счетные и несчетные.
Счётное множество есть бесконечное множество, элементы которого возможно пронумеровать натуральными числами. Счётное множество — это множество, равномощное множеству натуральных чисел.
Свойства счетных множеств:
Любое подмножество счётного множества либо конечно либо счётно
Объединение конечного или счётного числа счётных множеств счётно
Прямое произведение конечного числа счётных множеств счётно.
Множество всех конечных подмножеств счётного множества счётно.