9. Соотношение (неравенство) для плоских графов

Опишем классическую конструкцию Эйлера, связанную с плоскими графами. Пусть - плоский граф. Это означает, что имеется определенное изображение его на плоскости, в котором ребра пересекаются только в вершинах.

Классическая теорема Эйлера утверждает: если в плоском графе имеется «г» граней, «в» вершин и «р» ребер, то обязательно выполняется равенство: «г» + «в» - «р»=2.

Отсюда возникает множество соотношений для плоских графов, из которых остановимся только на одном, Фиксируем какой-нибудь плоский граф. Пусть в нем вершин и ребер. К этому графу можно, при необходимости, добавить ребра и получить снова плоский граф с тем же количеством вершин, но с увеличенным количеством ребер такой, что все грани в нем будут ограниченны треугольниками (включая внешнюю). Если - новое количество ребер и - количество граней в этом новом графе, то ; тогда теорема Эйлера приобретает вид: , но , так что , откуда 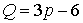, а для произвольного плоского графа, следовательно,

.

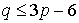10. Подграфы

Граф G’(V’,E’) называется подграфом графа G(V,E): G’(V’,E’) Í G(V,E), если V’Í V и E’Í E, и каждое из ребер E’ инцидентно только вершинам из V’.

Если G’Í G и множества вершин этих графов не равны, как и множества ребер, то подграф G’ является собственным подграфом графа G.

Если множества вершин этих графов совпадают и в графе G’ нет циклов, то G’ называется остовным подграфом (остовом, каркасом) графа G (т.е. он содержит все вершины исходного графа и некоторый поднабор его ребер).

Ñ Очевидно, что остов существует в каждом графе. Для его получения нужно удалить “лишние” ребра, разрушив циклы в каждой связной компоненте.

Остовный подграф для графа G можно построить не единственным образом. В общем, если (n,m)-граф G имеет k компонент связности, то для получения его остова из графа необходимо удалить (m–n+k) ребер.

Пример 3.23

Пример 3.10 (4,6)-граф G (а), его подграфы (б, в), причем б) – собственный подграф; 2 различных каркаса (г, д). Удаление ребер для получения остовного подграфа: (m–n+k) = 6 – 4 + 1 = 3. Þ из исходного графа требуется удалить 3 ребра (так, чтобы сохранились все вершины исходного графа и не стало циклов).

11. Максимальное число ребер в двудольном графе

Двудольный граф – граф, множество вершин которого можно разбить на два подмножества V1 и V2 так, что каждое ребро имеет один конец в V1, а другой в V2 . Двудольный граф G c такими подмножествами V1 и V2 обозначается как G(V1, V2, E).

Двудольный граф обыкновенный, если он не содержит параллельных ребер. Обыкновенный двудольный граф полный, если любая пара вершин из разных подмножеств соединена ребром (см. рис. 1). Полный двудольный граф содержит |Е|=|V2|×|V2| ребер.

Примеры двудольных графов

На рисунке изображены двудольный граф G=(V1, V2, E), обыкновенный двудольный граф G'=(V'1,V'2, E'), и полный двудольный граф G''=(V''1,V''2, E'').

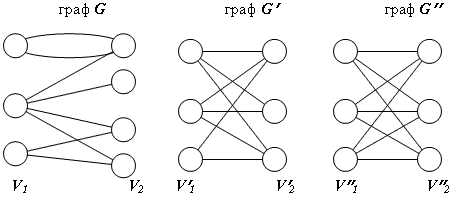
12. Способы задания графов

1. Явное задание графа как алгебраической системы.

2. Геометрический

3. Матрица смежности

4. Матрица инцидентности

Рассмотрим различные способы задания для одного и того же графа.

1. <{a,b,c,d},{u,v,w,x}; {(u,a),(u,b),(v,b),(v,c),(w,c),(w,a),(x,c), (x,d)}>. Так как мы рассматриваем только простые графы, граф нам проще определять как модель, носителем которой является множество вершин, а отношение – бинарное отношение смежности вершин. Тогда данный граф запишется как <{a,b,c,d}; {(a,b), (b,a),(b,c),(c,b),(a,c),(c,a),(c,d),(d,c)}>. В таком представлении ребру соответствуют две пары вершин (v1,v2) и (v2,v1), инцидентных данному ребру. Чтобы задать такое представление, достаточно для каждого ребра указать двухэлементное множество вершин – его мы и будем отождествлять с ребром. Для данного графа рёбра задаются множеством {{a,b},{b,c},{a,c},{c,d}} и граф мы будем записывать как пару (V,E), где V – множество вершин, а E – множество рёбер. В дальнейшем мы будем опираться именно на второе определение графа.

2. Геометрический

3. Матрица смежности

a b c d

a 0 1 1 0

b 1 0 1 0

c 1 1 0 1

d 0 0 1 0

4. Матрица инцидентности

u v w x

a 1 0 0 0

b 1 1 1 0

c 0 1 0 1

d 0 0 1 1

13. Операции над отношениями

Так как отношения, заданные на фиксированной паре множеств A, B, суть подмножества множества АхB , то совокупность всех этих отношений образует булеву алгебру относительно операций объединения, пересечения и дополнения отношений. В частности, для произвольных a A, b B.

Часто вместо объединения, пересечения и дополнения отношений говорят об их дизъюнкции, конъюнкции и отрицании.

Например, , , то есть объединение отношения строгого порядка с отношением равенства совпадает с отношением нестрого порядка, а их пересечение пусто. Кроме перечисленных важное значение имеют ещё операции обращения и умножения отношений, определяемые следующим образом.

Если , то обратным отношением называется отношение R − 1, определённое на паре B, A и состоящее из тех пар (b,a), для которых a R b. Например, < − 1 = > .Пусть теперь , . Произведением отношений R, S называется отношение такое, что

Если , и , то произведение отношений не определено. Если же отношения рассматривать определённые на каком-то множестве A, то такой ситуации не возникает. Например, рассмотрим отношение строгого порядка < определённого на множестве натуральных чисел. Несложно заметить, что

Бинарные отношения R и S называются перестановочными, если RS = SR. Несложно заметить, что для любого бинарного отношения R, определённого на A, RIA = IAR, где символом IA обозначено равенство, определённое на A. Однако равенство RR ^− 1 = I не всегда справедливо.

Имеют место следующие тождества:

R(ST) = (RS)T,

(RS)^ − 1 = S ^− 1R ^− 1,

,

,

,

,

.

Отметим, что аналоги последних двух тождеств для не имеют места.

Некоторые свойства отношения можно определить, используя операции над отношениями:

Рефлексивность: ,

Симметричность: ,

Транзитивность: .