Задача 6

В лотерее разыгрывается мяч стоимостью 3 руб. шахматы стоимостью 10 руб. и кеды стоимостью 5руб. Общее число билетов равно 20. Пусть  – размер выигрыша в рублях, тогда для данной случайной величины вычислите: математическое ожидание, медиану, дисперсию, среднее квадратичное отклонение, коэффициент асимметрии, коэффициент эксцесса, необходимые начальные и центральные моменты. Начертите многоугольник распределения и график функции распределения.

Величина  является дискретной случайной величиной и может принимать 4 значения: 0, 3, 5 и 10. Будем полагать, что среди 20 билетов три выигрышных, тогда вероятности распределятся следующим образом

Сведем вероятности в таблицу 1.

Таблица 1

	0	3	5	10
pi	0,85	0,05	0,05	0,05

Пользуясь таблицей 1, запишем закон распределения

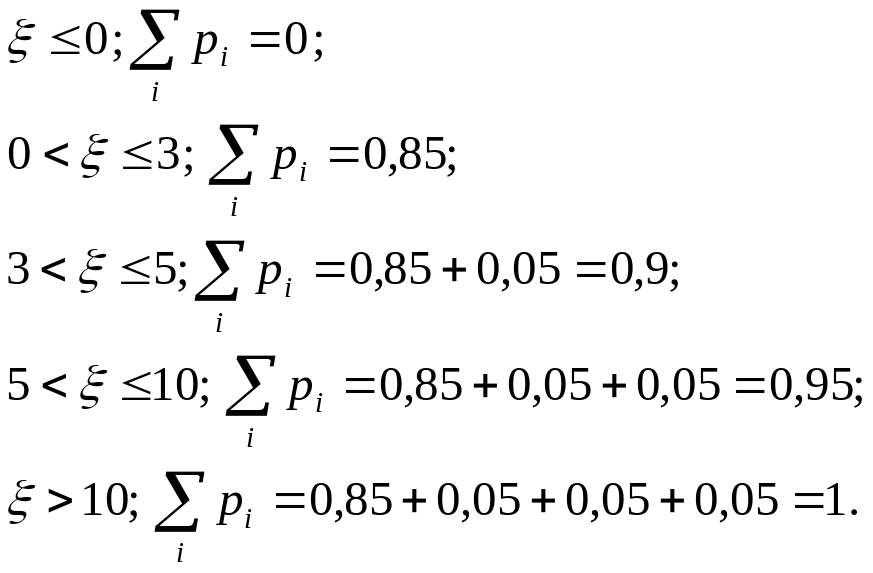
П ерепишем

	0 ,
	0,85 ,
	0,9 ,		(6.1)
	0,95 ,
	1 ,

Рассчитаем начальные моменты дискретной случайной величины, воспользовавшись следующей формулой

, (6.2)

где n – порядок начального момента.

Начальный момент первого порядка называется математическим ожиданием. Здесь и далее условимся его обозначать MX.

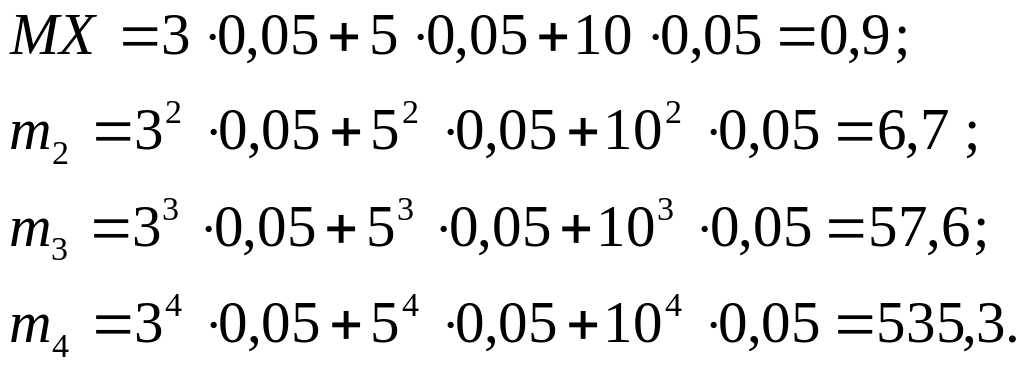
Рассчитаем центральные моменты дискретной случайной величины. Центральный момент второго порядка называется дисперсией. Здесь и далее условимся обозначать дисперсию DX.

Для расчета необходимых центральных моментов воспользуемся формулами сокращенного счета [2, стр. 99]

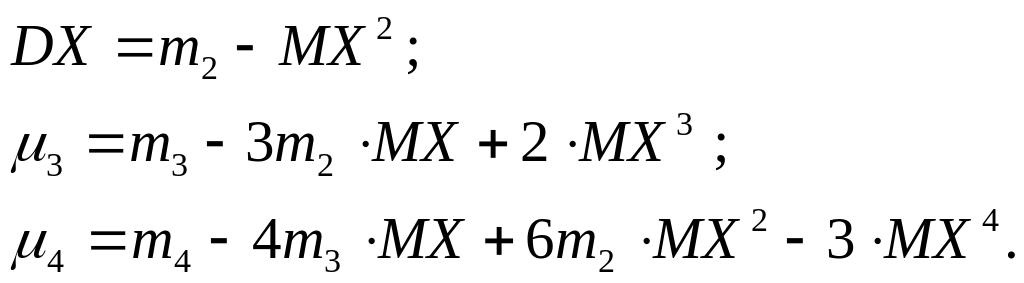(6.3)

Таким образом

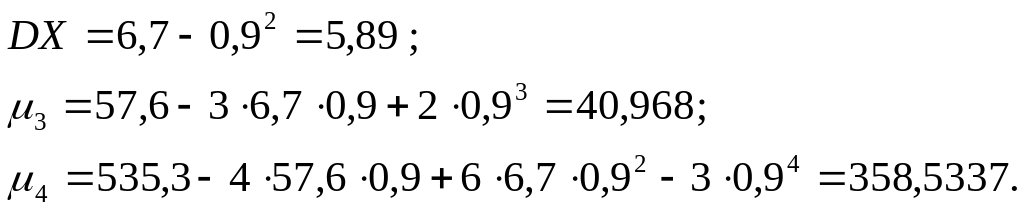
Определим среднее квадратичное отклонение, равное квадратному корню из дисперсии

.

Определим коэффициенты асимметрии и эксцесса

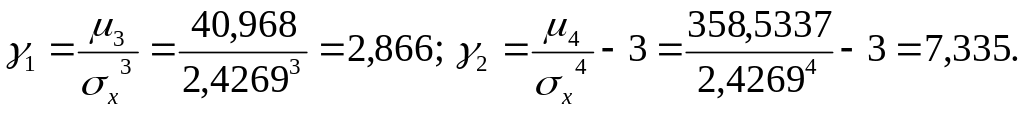
Из значений коэффициентов асимметрии и эксцесса можно сделать вывод, что случайная величина распределена несимметрично относительно математического ожидания и «островершинна» относительно нормального распределения.

Медианой случайной величины называется такое значение случайной величины, вероятность появления которого составляет 0,5. Глядя на (6.1) можно заключить, что медиана для данной случайной величины равна 0.

На рисунке 6.1 изображен многоугольник распределения случайной величины, построенный по таблице 1, а на рисунке 6.2 показан график функции распределения, построенный по (6.1).

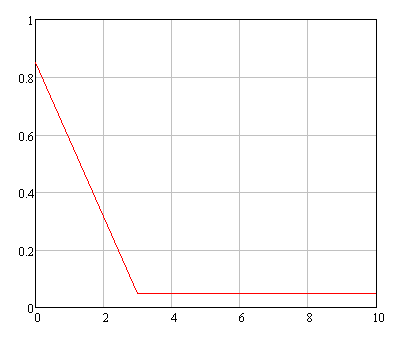
Рисунок 6.1 Многоугольник распределения

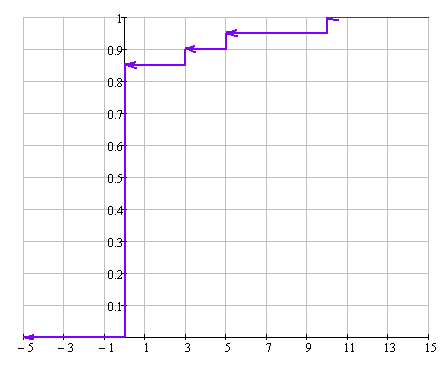
Рисунок 6.2 График функции распределения

Задача 7

Случайная величина  задана функцией плотности распределения

	0 ,
f(x)=	,	.	(7.1)
	0,

Определите: константу а, функцию распределения, необходимые начальные и центральные моменты, коэффициенты асимметрии и эксцесса, медиану. Определите вероятность попадания случайной величины в промежуток (, ), где =-/6 и =/4. Начертите графики функции распределения и плотности распределения.

Случайная величина  – непрерывная случайная величина. Определим функцию распределения, взяв определенный интеграл от плотности распределения (7.1).

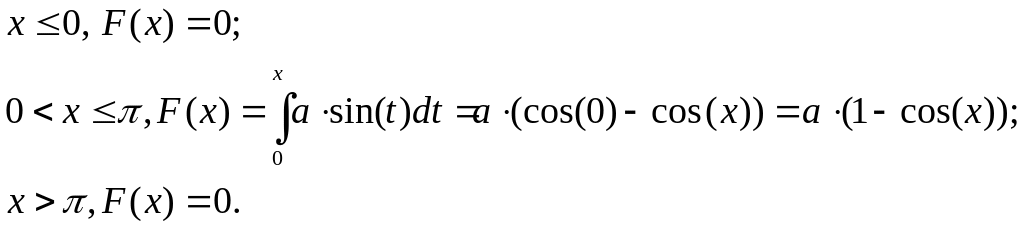
Перепишем

	0 ,
F(x)=	,	.	(7.2)
	1,

Зная, что F(x) равна единице при , найдем константу а.

Для непрерывной случайной величины начальные моменты n-го порядка будут определяться

. (7.3)

Таким образом, начальные моменты будут равны

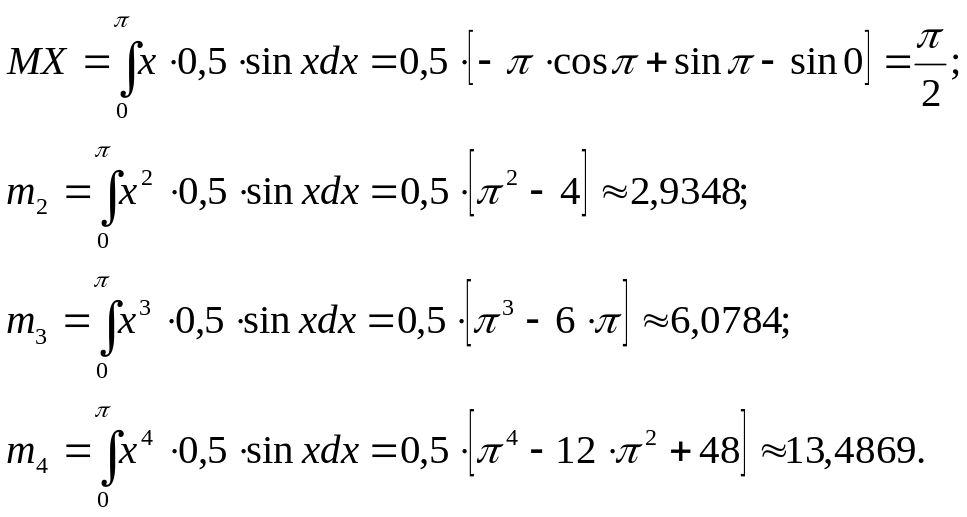
Определим центральные моменты, для чего воспользуемся формулами (6.3).

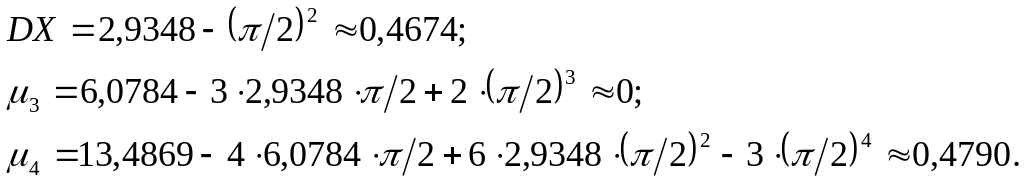
Тогда среднее квадратичное отклонение коэффициент асимметрии и коэффициент эксцесса определятся

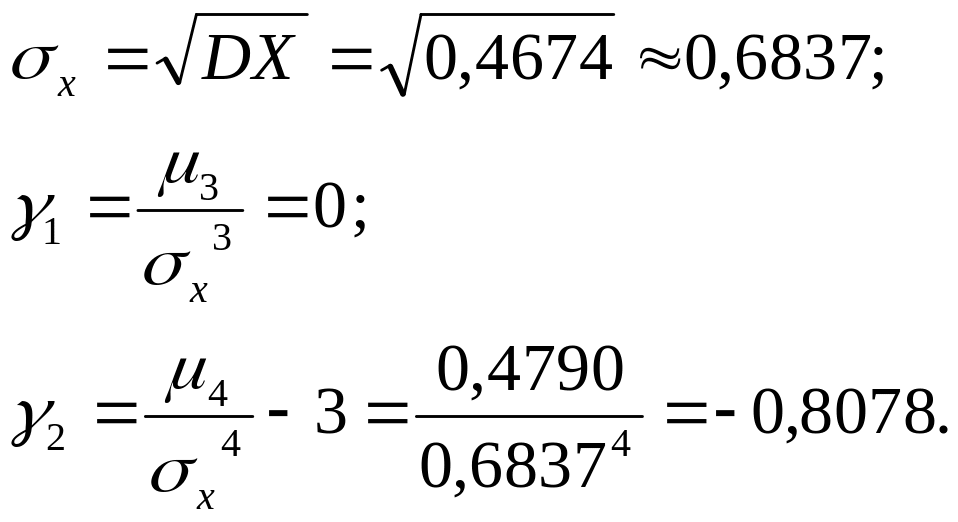
Из чего мы заключаем, что случайная величина распределена симметрично относительно математического ожидания, а её распределение несколько «приплюснуто» относительно нормального распределения.

Опираясь на предыдущий вывод, можно утверждать, что медиана и математическое ожидание совпадают, т.е.

.

Пользуясь функцией распределения (7.2), определим вероятность попадания случайной величины в интервал (, ).

На рисунке 7.1 показан график функции плотности распределения, построенный по (7.1), а на рисунке 7.2 показан график функции распределения, построенный по (7.2).

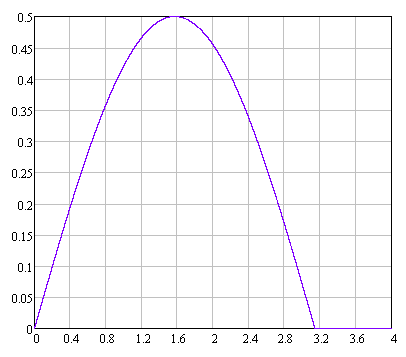
Рисунок 7.1 Плотность вероятности случайной величины

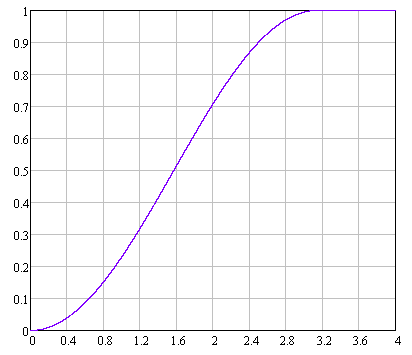
Рисунок 7.2 График функции распределения
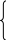