Задача 2
На отрезке [0;1] наудачу
ставятся две точки. Пусть
координаты первой точки, а
- второй точки. Рассматриваются следующие
события: А={вторая точка ближе к левому
концу отрезка, чем первая точка к
правому}; B={корни уравнения
![]() действительны}; С={max(,)0,5};
D={min(,)0,5}.
Привести соответствующие рисунки и
найти
действительны}; С={max(,)0,5};
D={min(,)0,5}.
Привести соответствующие рисунки и
найти
![]() .
.
Будем рассматривать точки в двумерном декартовом пространстве. Пусть будет независимой переменной. Представим события А, В, С и D в виде неравенств.
Событие А будет происходить, если
![]() .
.
Событие В будет происходить, если дискриминант уравнения будет больше, либо равен нулю, т.е.
![]() .
.
Событие С будет происходить, если
![]() .
.
Событие D будет происходить, если
![]()

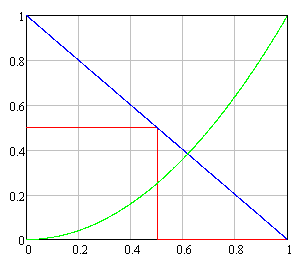
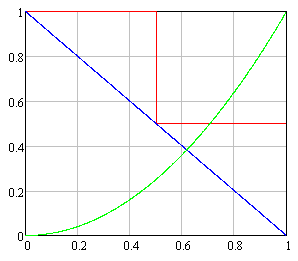
На рисунке 2.1 графически представлены множества исходов, благоприятствующих вышеназванным событиям.
|
|
|
|
Рисунок 2.1 a) событие А; б) событие В; в) событие С; г) событие D. |
|
Теперь найдем
множество
![]() ,
накладывая соответствующие области
согласно операциям над множествами.
Очевидно, что множество вырождается в
точку, т.е. вероятность
,
накладывая соответствующие области
согласно операциям над множествами.
Очевидно, что множество вырождается в
точку, т.е. вероятность
![]() .
.
Аналогично поступаем
с множеством
![]() .
На этот раз определенное множество.
Найдем площадь фигуры, которая очерчивает
границы множества.
.
На этот раз определенное множество.
Найдем площадь фигуры, которая очерчивает
границы множества.
![]()
Тогда согласно определению геометрической вероятности [2, стр. 27]
![]()
Здесь
![]() - это площадь квадрата, ограничивающего
генеральную совокупность исходов.
- это площадь квадрата, ограничивающего
генеральную совокупность исходов.
|
|
а)
Событие
|
б) Событие
|
Рисунок 2.2 |
|
В приложении А приведён листинг программы, производящей экспериментальный подсчет вероятностей указанных событий.
Задача 3
В окружность радиусом
1 с центром в начале координат наугад
бросается точка с координатами (,).
Какова вероятность того, что парабола
![]() пересечет обе оси координат.
пересечет обе оси координат.
Как и в задаче 2 поставим координату точки в зависимость от координаты . В этом случае необходимо найти такую функцию =(), которая очерчивала бы такое множество, попадая в которое парабола из условия пересекала бы обе оси координат. Также по условию видно, что значения и должны быть такими, чтобы неравенство
![]()
было верным.
Рассмотрим теперь параболу. Совершенно очевидно, что парабола пересекает ось ординат всегда. Ось абсцисс парабола пересекает, если уравнение
![]() (3.1)
(3.1)
имеет по крайней мере один действительный корень, т.е. дискриминант больше либо равен нулю.
Тогда запишем
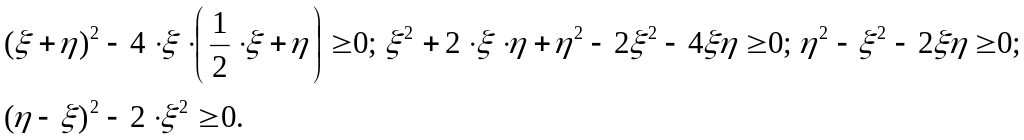
Таким образом, чтобы парабола пересекала обе оси должны выполняться следующие неравенства
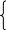
![]() (3.2)
(3.2)
Построим окружность радиусом 1 с центом в начале координат и две границы области, определяемых функциями
![]()
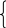
Подставляя произвольные точки, выделим части, в которых выполняется условие (3.2). На рисунке 3.1 показаны области, в которых выполняется условие (3.2).
Переходя в параметрическую систему координат, найдем площади данных секторов
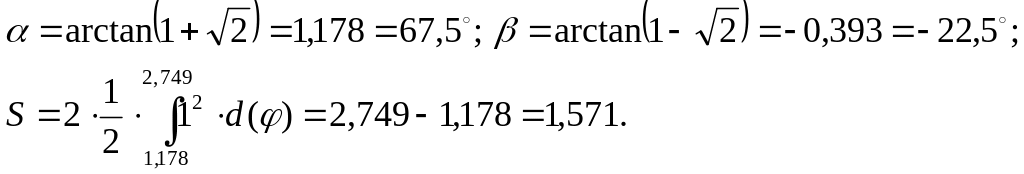
Тогда по определению геометрической вероятности
![]()

Рисунок 3.1 Генеральная совокупность исходов
В приложении А приведён листинг программы, производящей экспериментальные подсчёт указанной вероятности.

 a)
a) б)
б) в)
в)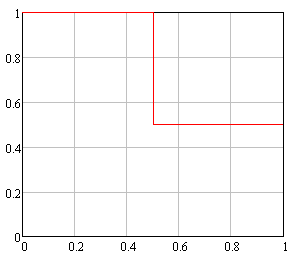 г)
г)