6 вопрос:. Момент инерции материальной точки относительно оси вращения - произведение массы этой точки на квадрат расстояния от оси. При заданной массе тела момент инерции зависит как от распределения этой массы по объему тела, так и от положения и направления оси вращения.Момент инерции твердого тела - это велина, характеризующая распределение массы в теле и являющаяся мерой инертности тела при вращательном движении. Формула момента инерции:

Единица момента инерции - килограмм-метр в квадрате.

Теорема Штейнера: Момент инерции тела относительно какой-либо оси равен моменту инерции относительно параллельной оси, проходящей через центр инерции, сложенной с величиной m*(R*R), где R - расстояние между осями.

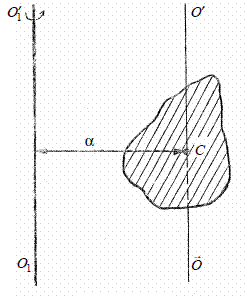
Угловое ускорение, которое тело приобретает под действием момента сил, прямо пропорционально результирующему моменту всех внешних сил, приложенных к телу, и обратно пропорциональна моменту инерции тела относительно некоторой оси.

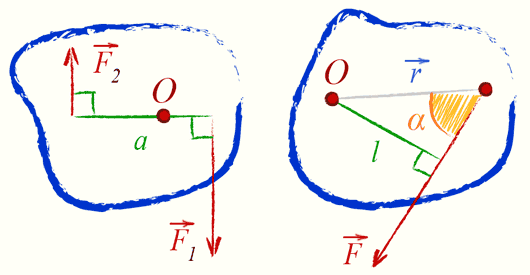
7 вопрос:. Сила приложенная к твердому телу, которое может вращаться вокруг некоторой точки, создает момент силы. Действие момента силы аналогично действию пары сил.

Момент силы

Момент силы относительно некоторой точки — это векторное произведение силы на кратчайшее расстояние от этой точки до линии действия силы.

Единица СИ момента силы:

1.	[M]= Ньютон · метр

Если: M — момент силы (Ньютон · метр), F — Приложенная сила (Ньютон), r — расстояние от центра вращения до места приложения силы (метр), l — длина перпендикуляра, опущенного из центра вращения на линию действия силы (метр), α — угол, между вектором силы F и вектором положения r, То

2.	M= F·l= F·r·sin(α)

или в виде векторного произведения

3.	→ M = → F · → r

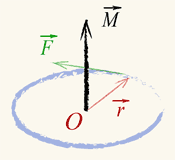М омент силы — аксиальный вектор. Он направлен вдоль оси вращения. Направление вектора момента силы определяется правилом буравчика, а величина его равна M.

Аксиальные векторы не связаны с определенной линией действия. Их можно перемещать в пространстве параллельно самим себе (свободные векторы).

8 Вопрос:

Свободные гармонические колебания в колебательном контуре

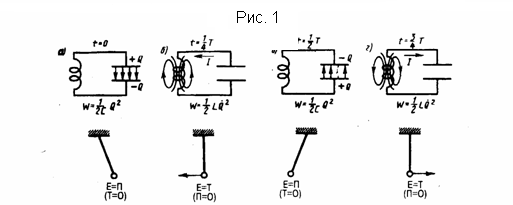
Среди исследований различных электрических явлений особое место занимают исследования электромагнитных колебаний. При колебательном процессе электрические физические величины (заряды, токи) периодически изменяются и процесс сопровождается взаимными превращениями электрического и магнитного полей. Для возбуждения и поддержания электромагнитных колебаний применяется колебательный контур — цепь, которая состоит из последовательно включенных резистора сопротивлением R, катушки индуктивностью L, и конденсатора емкостью С. Исследуем последовательные стадии колебательного процесса в идеализированном контуре, у которого сопротивление пренебрежимо мало (R≈0). Для возбуждения колебаний в контуре конденсатор предварительно заряжают, сообщая его обкладкам заряды ±Q. Следовательно, в начальный момент времени t=0 (рис. 1а) между обкладками конденсатора появится электрическое поле, энергия которого равна Q2/(2C) . Если конденсатор замкнуть на катушку индуктивности, то он начнет разряжаться, и в контуре начнет течь возрастающий со временем ток I. В результате энергия электрического поля будет падать, а энергия магнитного поля катушки (она равна (1/2)LI2 ) - увеличиваться. Так как R≈0, то, используя закон сохранения энергии, полная энергия поскольку полная энергия на нагревание не тратится. Поэтому в момент t=(1/4)T, когда конденсатор полностью разрядится, энергия электрического поля станет равной нулю, а энергия магнитного поля (а следовательно, и ток) достигает максимального значения (рис. 1б). Далее, начиная с этого момента ток в контуре будет уменьшаться; значит, начнет уменьшаться магнитное поле катушки, и в ней индуцируется ток, который течет (по правилу Ленца) в том же направлении, что и ток разрядки конденсатора. Далее, начнет перезаряжаться конденсатор, появится электрическое поле, которое будет стремиться ослабить ток, который в конце концов станет равным нулю, а заряд на обкладках конденсатора станет максимальным (рис. 1в). Далее те же процессы будут протекать в обратном направлении (рис. 1г) и к моменту времени t=Т система придет в первоначальное состояние (рис. 1а). После этого рассмотренный цикл разрядки и зарядки конденсатора будет повторяться. Если бы в контуре потерь энергии не было, то совершались бы периодические незатухающие колебания, т.е. периодически изменялись (колебались) бы заряд Q на обкладках конденсатора, сила тока I, текущего через катушку индуктивности и напряжение U на конденсаторе . Значит, в контуре появляются электрические колебания, причем колебания сопровождаются превращениями энергий электрического и магнитного полей. С электрическими колебаниями в колебательном контуре можно провести аналогию с механическими колебаниями маятника (рис. 1 внизу), которые сопровождаются взаимными превращениями кинетической и потенциальной энергий маятника (на рисунке Е - кинетическая энергия, П - потенцияльная). В данном случае энергия электрического поля конденсатора Q2/(2C) аналогична потенциальной энергии маятника, энергия магнитного поля катушки (LQ2/2) — кинетической энергии, сила тока в контуре — скорости движения маятника. Индуктивность L аналогична массе m, а сопротивление контура — силе трения, которая действуюет на маятник. По закону Ома, для контура, который содержит резистор сопротивлением R, катушку индуктивностью L, и конденсатор емкостью С где IR—напряжение на резисторе, UC = Q/C - напряжение на конденсаторе, ξs = -L(dI/dt) – э.д.с. самоиндукции, которая возникает в катушке при протекании в ней переменного тока (ξs – единственная э.д.с. в контуре). Значит, (1) Разделив формулу (1) на L и подставив и получим дифференциальное уравнение колебаний заряда Q в контуре: (2) В рассматриваемом колебательном контуре внешние э.д.с. отсутствуют, значит колебания в контуре представляют собой свободные колебания. Если сопротивление R=0, то свободные электромагнитные колебания в контуре будут гармоническими. Тогда из (2) найдем дифференциальное уравнение свободных гармонических колебаний заряда в контуре: Из формулы (1) следует, что заряд Q гармонически колеблеься по закону (3) где Qm — амплитуда колебаний заряда конденсатора с циклической частотой ω0, которая называется собственной частотой контура, т. е. (4) и периодом (5) Выражение (5) впервые было получено У. Томсоном и называется формулой Томсона. Сила тока в колебательном контуре (6) где Im = ω0Qm — амплитуда силы тока. Напряжение на конденсаторе равно (7) где Um=Qm/C - амплитуда напряжения. Из формул (3) и (6) вытекает, что колебания тока I опережают по фазе колебания заряда Q на π/2, т.е., когда ток равен максимальному значению, заряд (а также и напряжение (7)) обращается в нуль, и наоборот.

9 вопрос: Из сказанного в § 17 следует, что в тех случаях, когда тело, действуя на другое тело, вызывает его перемещение, а направление силы при этом не перпендикулярно направлению перемещения, совершается механическая работа. Наблюдения показывают, что при определенных условиях работа может быть совершена любым телом. Например, сжатая или растянутая пружина, действующая силой упругости на прикрепленное к ней тело, перемещает его и при этом совершает механическую работу. Может совершать работу и любое движущееся тело. Сталкиваясь с другим телом, оно действует на него силой и может вызвать перемещение этого тела или его частей (деформацию). При этом тоже совершается механическая работа.

Про тела, которые могут совершать работу, говорят, что они обладают энергией. Энергией называют скалярную физическую величину, показывающую, какую работу может совершить тело. Энергия равна той максимальной работе, которую тело может совершить в данных условиях. Механическая работа является мерой изменения энергии в различных процессах. Поэтому энергию и работу выражают в одних и тех же единицах (в СИ - в джоулях). В более общем смысле энергия - это единая мера разных форм движения материи, а также мера перехода движения материи из одной формы в другую. Для характеристики конкретных форм движения материи используют понятия о соответствующих видах энергии: механической, внутренней, электромагнитной и т. д. Механическая энергия является характеристикой движения и взаимодействия тел. Она зависит от скоростей и взаимного расположения тел.

Кинетическая энергия

Рассмотрим случай, когда тело массой m под действием постоянной силы (F=const) движется прямолинейно равноускоренно (а=const). Определим работу силы, приложенной к телу, при изменении модуля скорости этого тела от v₁ до v₂.

Как было отмечено в §17, работу постоянной силы вычисляют по формуле А=Fscos. Так как в рассматриваемом нами случае направление силы F и перемещения s совпадают, то cos=1 и А=Fs. По второму закону Ньютона F=ma. В § 2 было показано, что для прямолинейного равноускоренного движения справедлива формула

v₂=v_o²+2as.

Из этой формулы при v_о=v₁ и v=v₂ Следует, что

s=(v₂²-v₁²)/2a.

Подставив значения F и s в формулу работы, получим

А=mv₂²/2-mv₁²/2    (3.12).

Из последней формулы видно, что работа силы, приложенной к телу, при изменении скорости этого тела равна разности двух значений некоторой величины mv₂²/2.

Выше отмечалось, что механическая работа есть мера изменения энергии. Следовательно, в правой части формулы (3.12) стоит разность двух значений энергии данного тела. Это значит, что величина mv₂²/2 представляет собой энергию, обусловленную движением тела. Эту энергию называют кинетической. Она обозначается W_к. Следовательно,

W_к=mv₂²/2.    (3.13)

С учетом (3.13) формулу (3,12) можно записать в виде

А=W_k2-W_k1=W_k,    (3.14)

т.е. работа, совершаемая силой при изменении скорости тела, равна изменению кинетической энергии этого тела.

Когда направление силы совпадает с направлением перемещения тела, работа силы положительна (т.е. A>0). Из формулы (3.14) видно, что в этом случае W_k2-W_k1>0, т.е. W_k2>W_k1. Следовательно, когда сила совершает положительную работу, кинетическая энергия тела увеличивается. Когда же направление силы противоположно направлению перемещения, то A<0 и W_k2-W_k1<0, т.е. W_k2<W_k1. Следовательно, когда сила совершает отрицательную работу, кинетическая энергия тела уменьшается.

Потенциальная энергия

О пределим работу, совершаемую силой тяжести F_т при переносе материальной точки массой m по криволинейной траектории ВС из одной точки В поля тяготения Земли в другую точку С (рис 31). Для этого разобьем траекторию движения тела на сколь угодно малые участки s_k, каждый из которых можно считать прямолинейным.

На произвольно выбранном таком участке сила тяжести F_т составляет с перемещением s_k угол _k. Поэтому на данном участке работа силы тяжести

A_k=F_т·s_k·cos(_k).    (3.15)

Спроецируем участок s_k на вертикаль BD. Его проекция

h_k=s_k·cos(_k).    (3.16)

Из (3.15) и (3.16) имеем A_k=F_т·h_k. Очевидно, что работа A_BC силы тяжести F_т на всем пути ВС равна сумме элементарных работ h_k на всех участках s_k этого пути:

ABC=F_т(h₁-h₂)=mgh₁-mgh₂    (3.17)

Из последней формулы видно, что работа силы тяжести при переносе материальной точки массой m в поле тяготения Земли равна разности двух значений некоторой величины mgh. Поскольку работа есть мера изменения энергии, то в правой части формулы (3.17) стоит разность двух значений энергии этого тела. Это значит, что величина mgh представляет собой энергию, обусловленную положением тела в поле тяготения Земли.

Энергию, обусловленную взаимным расположением взаимодействующих между собой тел (или частей одного тела), называют потенциальной и обозначают W_п. Следовательно, для тела, находящегося в поле тяготения Земли,

W_п=mgh.    (3.18)

С учетом (3.18) формулу (3.17) можно записать в виде

A_BC=W_п1-W_п2=-(W_п2-W_п1)=-W_п    (3.19)

т. е. работа силы тяжести равна изменению потенциальной энер-гии тела, взятому с противоположным знаком.

Из рис. видно, что работа A_BD, совершаемая силой тяжести при перемещении материальной точки массой m из точки B в точку D по вертикали ВD, составляет A_BC=mgh₁-mgh₂. Следовательно, A_BD=A_BC. Таким образом, работа силы тяжести не зависит от траектории движения тела, а определяется лишь положением в поле тяготения Земли начальной и конечной точек перемещения тела.

В § 12 отмечалось, что силы, работа которых не зависит от траектории движения тела, называют консервативными, а поле таких сил называется потенциальным. Сила тяжести является консервативной, а поле тяготения - потенциальным. Из формулы (3.19) следует, что работа консервативных сил равна изменению потенциальной энергии тела, взятому с противоположным знаком.

Следует отметить, что тела имеют потенциальную энергии не только вследствие их притяжения к Земле. В § 10 было показано, что в результате упругой деформации тело тоже приобретает потенциальную энергию. Если, например, сжимается или растягивается упругая пружина, то ее потенциальная энергия вычисляется по формуле W_п=kх²/2, где k - жесткость пружины, x - ее удлинение, т.е. смещение точки приложения силы упругости. Работа силы упругости определяется по формуле

A=W_п1-W_п2= kх₁²/2- kх₂²/2=-W_п    (3.20)

Сумму кинетической и потенциальной энергии тела называют полной механической энергией этого тела и обозначают W.

W=W_п+W_k    (3.21)

10 вопрос: Колеблющееся тело может принимать участие в нескольких колебательных процессах, тогда следует найти результирующее колебание, другими словами, колебания необходимо сложить. В данном разделе будем складывать гармонические колебания одного направления и одинаковой частоты применяя метод вращающегося вектора амплитуды, построим графически векторные диаграммы этих колебаний (рис. 1). Tax как векторы A₁ и A₂ вращаются с одинаковой угловой скоростью ω₀, то разность фаз (φ₂ - φ₁) между ними будет оставаться постоянной. Значит, уравнение результирующего колебания будет (1) В формуле (1) амплитуда А и начальная фаза φ соответственно определяются выражениями (2) Значит, тело, участвуя в двух гармонических колебаниях одного направления и одинаковой частоты, совершает при этом также гармоническое колебание в том же направлении и с той же частотой, что и складываемые колебания. Амплитуда результирующего колебания зависит от разности фаз (φ₂ - φ₁) складываемых колебаний.

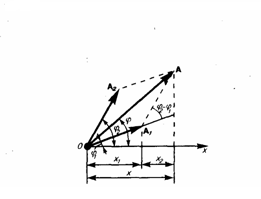
Рис.1

Исследуем выражение (2) в зависимости от разности фаз (φ₂ - φ₁): 1) φ₂ - φ₁ = ±2mπ (m = 0, 1, 2, ...), тогда A=A₁+A₂, т. е. амплитуда результирующего колебания А будет равна сумме амплитуд складываемых колебаний; 2) φ₂ - φ₁ = ±(2m+1)π (m = 0, 1, 2, ...), тогда A=|A₁–A₂|, т. е. амплитуда результирующего колебания будет равна разности амплитуд складываемых колебаний. Для практики представляет особый интерес случай, когда два складываемых гармонических колебания одинакового направления мало отличаются по частоте. После сложения этих колебаний получаются колебания с периодически изменяющейся амплитудой. Периодические изменения амплитуды колебания, которые возникают при сложении двух гармонических колебаний с близкими частотами, называются биениями. Пусть амплитуды складываемых колебаний равны А, а частоты равны ω и ω+Δω, причем Δω<<ω. Выберем начало отсчета так, чтобы начальные фазы обоих колебаний были равны нулю: Складывая эти выражения и учитывая, что во втором сомножителе Δω/2<<ω, получим (3) Результирующее колебание (3) можно считать как гармоническое с частотой ω , амплитуда А_σ которого изменяется по следующему периодическому закону: (4) Частота изменения А_σ в два раза больше частоты изменения косинуса (так как берется по модулю), т. е. частота биений равна разности частот складываемых колебаний: Период биений Вид зависимости (3) показан на рис. 2, где сплошные жирные линии представляют график результирующего колебания (3), а огибающие их линии - график медленно меняющейся согласно уравнению (4) амплитуды.

Рис.2

Нахождение частоты тона (звука определенной высоты) биений между эталонным и измеряемым колебаниями — наиболее часто используемый на практике метод сравнения измеряемой величины с эталонной. Метод биений применяется для настройки музыкальных инструментов, анализа слуха и т. д. При исследовании сложного колебательного процесса нужно знать, что любые сложные периодические колебания s=f(t) можно представить в виде суперпозиции (наложения) одновременно совершающихся гармонических колебаний с различными амплитудами, начальными фазами, а также частотами, которые кратны циклической частоте ω₀ : (5) Представление в виде (5) любой периодической функции связывают с понятием гармонического анализа сложного периодического колебания, или разложения Фурье. Слагаемые ряда Фурье, которые определяют гармонические колебания с частотами ω₀, 2ω₀, 3ω₀, ..., называются первой (или основной), второй, третьей и т. д. гармониками сложного периодического колебания.

11 вопрос: Термодинамические параметры.

 Уравнение состояния идеального газа

В термодинамике рассматриваются термодинамические системы, т.е. макроскопические объекты, которые могут обмениваться энергией как друг с другом, так и с внешней средой. Для описания состояния термодинамической системы вводятся физические величины, которые называются термодинамическими параметрами или параметрами состояния системы. Обычно в качестве термодинамических параметров выбирают давление P, объем V и температуру T.

Температура – это макроскопический параметр, характеризующий различную степень нагретости тел. Это одна из макроскопических характеристик внутреннего состояния тел. Понятие температуры имеет смысл для равновесных состояний термодинамической системы. Равновесным состоянием (состоянием термодинамического равновесия) называется состояние системы, не изменяющееся с течением времени (стационарное состояние), причем стационарность состояния не связана с процессами, происходящими во внешней среде. Равновесное состояние устанавливается в системе при постоянных внешних условиях и сохраняется в системе произвольно долгое время. Во всех частях термодинамической системы, находящейся в состоянии термодинамического равновесия, температура одинакова.

Для измерения температуры используются зависимости некоторых физических параметров вещества от температуры. Такими параметрами могут быть объем, линейные размеры жидкостей и твердых тел, давление газа в замкнутом объеме, электрическое сопротивление, цвет тела и др. В термодинамической шкале температур температура измеряется в кельвинах ( К ) и обозначается Т .

Соотношение, устанавливающее связь между параметрами состояния системы называется уравнением состояния термодинамической системы. Если какой либо из термодинамических параметров системы изменяется, то происходит изменение состояния системы, называемое термодинамическим процессом . Термодинамический процесс называется равновесным, если система бесконечно медленно проходит непрерывный ряд бесконечно близких термодинамических равновесных состояний. Изопроцессами называются термодинамические процессы, происходящие в системе с постоянной массой при каком либо одном постоянном параметре состояния.

Идеальным газом называется газ, молекулы которого не взаимодействуют друг с другом на расстоянии и имеют исчезающе малые собственные размеры. Состояние заданной массы m идеального газа определяется значениями трёх параметров: давления P, объёма V, и температуры Т. Соотношение, устанавливающее связь между этими параметрами, имеет вид:

   -

где М - масса 1 моля газа, R = 8,31 - универсальная газовая постоянная.

Для одного моля газа уравнение состояния идеального газа примет вид:

   - уравнение Клапейрона.

Рассмотрим теперь изопроцессы для идеального газа:

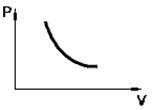
T = const – изотермический процесс.

PV = const – закон Бойля-Мариотта.

P = const - изобарический процесс.

  - закон Гей-Люссака.

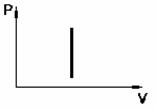
V = const – изохорический процесс ,

- закон Шарля.

Запишем уравнение состояния идеального газа в другой форме.Введем новую постоянную величину:   - постоянная Больцмана.

Давление, оказываемое газом на грань куба, равно: 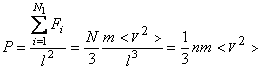,где n – концентрация молекул.

На каждую степень свободы молекулы приходится в среднем одинаковая кинетическая энергия равная  (k-постоянная Больцмана).

Числом степеней свободы i системы называется количество независимых величин, с помощью которых может быть задано положение системы.

Основы статистической физики Все тела состоят из огромного числа частиц, движение которых хаотично и сопровождается массовыми столкновениями.

От распределения молекул по скоростям  можно перейти к распределению молекул по их кинетической энергии . Для этого надо в распределении молекул по скоростям выразить  и  через  и .

Для нахождения можно воспользоваться выражением для средней кинетической энергии <e> поступательного движения молекул  ,

Распределение Больцмана молекул по их потенциальным энергиям Если газ находится во внешнем силовом поле, то частицы газа обладают потенциальной энергией п .

Основы физической кинетики Явления переноса.

Длина свободного пробега молекулы – это путь l, который молекула проходит между двумя последовательными соударениями.

Вакуум Мы получили, что средняя длина свободного пробега обратно пропорциональна давлению Р, т.е. с уменьшением давления средняя длина свободного пробега увеличивается.

Теплопроводность газов Рассмотрим газ, в котором каким-то способом поддерживается непостоянство температуры вдоль направления, которое мы обозначим буквой x.

При изучении этого раздела следует иметь в виду, что колебания различной физической природы описываются с единых математических позиций. Здесь надо четко уяснить такие понятия, как гармоническое колебание, фаза, разность фаз, амплитуда, частота, период Диффузия в газах