14. Определение силы неравномерного давления на криволинейную поверхность (p≠const, n≠const)
Силу
весового давления
опред. по ее пр-циям. Гориз. пр-ция
,
где
– пр-ция площадки dS
на вертик. пл-ть, нормальную к оси х.
Послед. интеграл предст. собой статический
момент площади
отн-но оси y.
Следовательно,
,где
–
координата центра тяж. площади
.
Т.
о., чтобы вычислить гориз. пр-цию
силы
весового давл-я на кривол-ую пов-ть,
следует площадь проекции
этой пов-ти на пл-ть, нормальную к рассм-ой
гориз-ой оси, умножить на давление в
центре тяжести площади
.
Пр-ция
силы весового давления на вертик-ю ось
опред-ся
,
где
–
пр-ция на пл-ть х0у
пов-ти
S.
Посл-й
интеграл предст. собой объем тела
,
ограниченного пов-тью
S,
цил-ой бок. пов-тью
с вертик-ми образующими и пр-цией
кривол-ой пов-ти
S
на свободную пов-ть жидкости. Это тело
наз. телом давл-я, а величина
есть вес жидк. в его объеме.
13. Определение силы неравномерного давления на плоскую стенку
Опред.
результирующую силу избыточных давлений
,
которые созд-ся внеш. избыточным
и весовым
давлениями. Заменим внеш. давление
воздействием эквивалентного слоя
жидкости, толщина, которого
опред-ся высотой поднятия жидкости в
пьезометре
Величину силы вычислим по ф-ле (1):
давление: 
,(2)
ч
то
при подстановке в формулу
(1)
дает:
Интеграл
представляет собой статический момент
площади
S
относительно
оси Ох,
равный, как известно, произведению
S
на координату
ее центра тяжести.
Поэтому получим (3):
Вектор
силы
направлен по нормали к стенке S,
линия действия этой силы пересекает
стенку в некоторой точке
D,
называемой центром давления. Для
отыскания координат этой точки (
)
используем теорему о равенстве момента
равнодействующей и суммы моментов
составляющих, которая в данном случае
выражается уравнением:
где
и
–
радиус-векторы соответственно центра
давления D
и произвольной точки (ху)
площади
S.
По правилам составления проекций векторного произведения находим
; 
.
Учитывая выражения (2 и (3), получим:
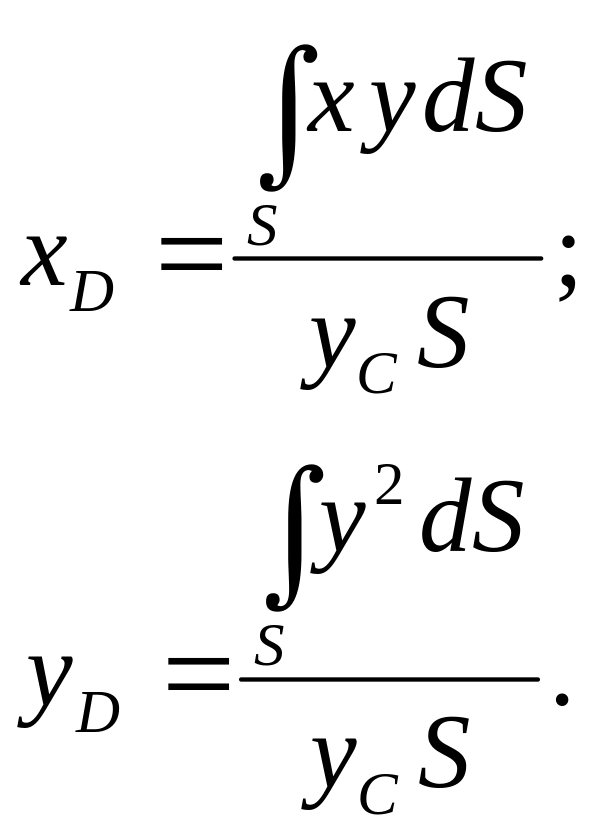
31 Уравнения движения идеальной жидкости в форме Громеки-Лэмба, их интеграл для установившегося движения.
Если
в правую часть уравнений Эйлера подставить
ускорение в виде
или
,
то это приводит к уравнению движения в
форме Громеки-Лэмба. Для установившегося
движения имеем
Поскольку
является
полным дифференциалом, то можно
записать
,где
Ф – силовая ф-ция.Сопоставляяих получаем
.С
другой стороны вектор
Из
этого следует, что
.
С учетом этого выраженияуравнению
Громеки-Лэмба принимает вид
.Следует
иметь в виду, что эта форма записи
справедлива лишь для несжимаемой
жидкости, т.е. при условии
.уравнению
движения можно придать более удобную
для анализа форму, умножив скалярно его
левую и правую части на произвольный
направленный отрезок
И
получим конечный результат: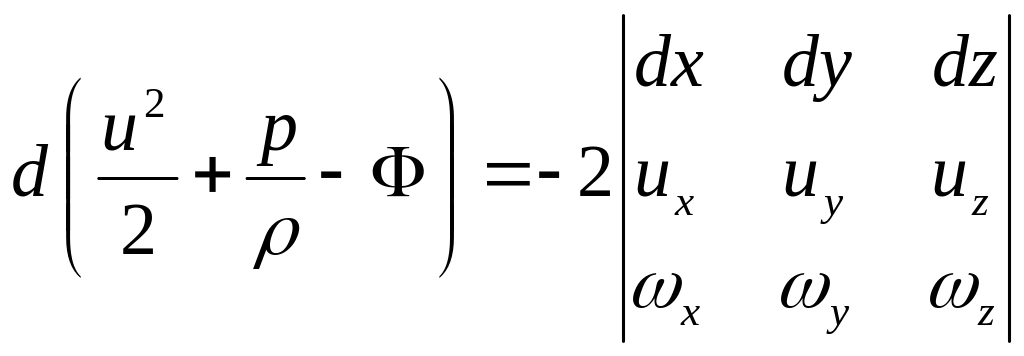
Интегрирование уравнения движения возможно лишь в случае, когда его правая часть равна нулю.Исходя из физического смысла величин, составляющих определитель, имеем четыре возможных случая:
;
;
;
.Для
любого из них можем записать
И
после интегрирования:
Если
из массовых сил действует только сила
тяжести, то, как было показано при
рассмотрении гидростатики,
и
интегральное выражение принимает вид
Еще раз обратим внимание на то, что вид уравнения одинаков вне зависимости от того, какой из четырех случаев равенства нулю определителя рассматривается. Однако смысл интеграла и область его применения различны.Первый случай является признаком потенциальности движения. Интеграл называют интегралом Коши-Лагранжа. Он справедлив для любых точек жидкости, движущейся без вращения частиц, т.е. потенциально.
Второй случай является признаком коллинеарности вектора вихря и вектора скорости. Третий случай характеризует движение жидкой частицы вдоль вихревой линии, а четвертый - движение вдоль линии тока. Интеграл при этом носит название интеграла Бернулли. Он справедлив как для потенциального, так и для вихревого движений, но только вдоль линии тока