
- •Элементы новизны содержания учебного материала
- •Воспитание познавательной активности (поиск математических закономерностей)
- •Выявление межпредметных связей
- •Математика и физика.
- •Математика и химия
- •Математика и экономика
- •Создание проблемной ситуации
- •Раскрытие красоты математических закономерностей
- •Использование алгоритмов
- •Задачи на нахождение.
- •Задачи на доказательство.
- •Задачи, несущие новую информацию и их типы.
- •Задачи с жизненным содержанием.
- •Логические задачи
Задачи на доказательство.
Задача 31. Докажите, что если сумма двух натуральных чисел меньше 13, то их произведение не больше 35.
Доказательство: Пусть произведение двух натуральных чисел больше 36; тогда одно из них больше 6 (так как если оба множителя не больше 6, то их произведение не больше 36). Если одно слагаемое больше 6, то оно может быть равно 7, 8, 9, 10 или 11; тогда другое слагаемое соответственно не больше 5, 4, 3, 2 или1. В каждом из этих случаев произведение не больше 35, 32, 27, 20 или 11. Это противоречит сделанному предположению, что и требовалось доказать.
Задача 32. Докажите, что число 7777+1 не делится на 5.
Доказательство:
Число 7777 + 1 = (74)194 73
+ 1 = 2401194
343+1
не делится на 5, так как оканчивается
на 4.
73
+ 1 = 2401194
343+1
не делится на 5, так как оканчивается
на 4.
Задача33. Докажите, что 129*70 делится на 6.
Доказательство:
129:3(так как сумма цифр делится на 3)
70:2, значит 129*70 делится на 6.
Г. Ленгауэр, рассказывая о зале математических развлечений в г. С.-Петербурге, приводит наборы различных занимательных математических задач. Они подбираются последующим группам:
1.) Задачи, не требующие или почти не требующие математических знаний и основанные на сообразительности и догадке.
2.) Задачи требующие, кроме смекалки, еще и элементарных математических знаний или заставляющие вспомнить эти знания, когда-то полученные в школе.
3.) Вопросы и задачи, имеющие целью проверку и уточнение математических знаний школьника. Это главным образом неожиданные сопоставления и выводы, иногда парадоксы и т. п.
Задача34. Множимое увеличили на 10%, а множитель уменьшили на 10%.Как при этом изменилось произведение?
Пусть множимое х, а множитель у; тогда новое множимое 1,1х, а 0,9у – новый множитель. Новое произведение равно 0,99ху, следовательно, произведение уменьшилось на 1%.
Задача
35. Количество отсутствующих
учеников в классе составляет
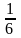 числа присутствующих. После того, как
из класса вышел один ученик, число
отсутствующих стало равно
числа присутствующих. После того, как
из класса вышел один ученик, число
отсутствующих стало равно
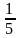 числа присутствующих. Сколько учеников
в классе?
числа присутствующих. Сколько учеников
в классе?
Решение:
Пусть а – количество
учеников в классе. Первоначально число
отсутствующих составляло
 часть от а. После того, как из класса
вышел один ученик, число отсутствующих
составило
часть от числа а. Поэтому один ученик
соответствует
-
=
часть от а. После того, как из класса
вышел один ученик, число отсутствующих
составило
часть от числа а. Поэтому один ученик
соответствует
-
= часть от а. Следовательно, в классе
42 ученика.
часть от а. Следовательно, в классе
42 ученика.
4.) Серия для любителей трудных и остроумных математических задач. Эти задачи для своего решения требуют достаточной математической подготовки, однако не выходят из объема курса средней школы.
Пример 36. Путь от дачи до города идет сначала горизонтально, а затем в гору. Дачник проехал на велосипеде горизонтальную часть пути со скоростью10 км/ч, а в гору шел пешком со скоростью3 км/ч и прибыл в город через 1 ч 40 мин после выезда с дачи. Обратно он проехал путь под гору со скоростью 15 км/ч, а горизонтальную часть пути со скоростью 12 км/ч и прибыл на дачу через 58 мин после выезда из города. Сколько километров от дачи до города?
Р ешение:
3км/ч
Г
ешение:
3км/ч
Г
10км/ч 15км/ч
Д 12км/ч О
Пусть: х
км – составляет горизонтальный
участок(ДО), у км – подъем (ОГ), тогда
время которое он затратил на путь от
дачи до города: (
 +
+
 )ч , а время
которое он затратил на путь с города
до дачи :
+
)ч , а время
которое он затратил на путь с города
до дачи :
+
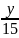 )ч
. По условию задачи, дачник прибыл
в город через 1 ч 40 мин , а на обратный
путь затратил 58 мин после выезда из
города.
)ч
. По условию задачи, дачник прибыл
в город через 1 ч 40 мин , а на обратный
путь затратил 58 мин после выезда из
города.
Составим и решим систему уравнений.
 +
= 1
+
= 1
 *30
*30
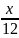 +
=
+
=
 *60
*60
3 х
+10у = 50
х
+10у = 50
5х + 4у = 58
Находим: у = 2 ,х = 10
2 + 10 = 12 ( км)
Ответ: 12 километров путь от дачи до города
5.)Задачи для ребят в возрасте 8—12 лет.
Задача 37. Из чисел 21, 19, 30, 25, 3, 12, 9, 15, 6, 27, выбрать три такие числа, сумма которых равна 50.
Ответ. Сумма чисел 19, 25 и 6 равна 50
Задача 38. Продолжите ряд чисел: 10,8,11,9,12,10 до восьмого числа. По какому правилу он составлен?
Ответ: 10, 8, 11, 9, 12, 10, 13, 11,… . Правило следующее: на нечетных местах ряда стоят последовательные натуральные числа, начиная с 10, а на четных – начиная с 8.
6.) Задачи-шутки, математические фокусы и развлечения.
М. Гарднер в книге «Есть идея!» [43] разделил собранные в ней задачи на шесть категорий:
комбинаторные,
геометрические,
теоретико-числовые,
логические,
процедурные
словесные.
При этом он отмечает, что данные категории задач не взаимоисключающие, они неизбежно перекрываются, и задачи, отнесенные к одной из них, можно было бы включать и в другие.
Комбинаторные:
Задача 39. Имеется пять одинаковых стульев и обивочная ткань трех разных цветов. Сколько существует вариантов обивки, если каждый стул можно обить тканью любого цвета?
Решение. Стулья одинаковы, поэтому два варианта обивки будут различаться только в том случае, если тканью хотя бы одного цвета обито разное количество стульев.
Закодируем обивочные ткани номерами 1, 2 и 3. Тогда все варианты обивки будут наборами из пяти цифр, отличающимися друг от друга количеством единиц, двоек или троек. Выпишем в первой строке набор из пяти единиц, во второй строке — все наборы с 4 единицами, в третьей — с тремя единицами и т.д. и, наконец, в последней, шестой строке — все наборы без единиц:
11111,
11112, 11113,
11122, 11123, 11133,
11222, 11223, 11233, 11333,
12222, 12223, 12233, 12333, 13333,
22222, 22223, 22233, 22333, 23333, 33333.
Таким образом, всего существует 1 + 2 + 3 + 4 + 5 + 6 = 21 вариант обивки.
Задача 40. Сколькими способами можно расположить на шахматной доске 2 ладьи так, чтобы они не били друг друга?
Решение. Ладья бьет любое поле на той горизонтали и на той вертикали, где она стоит. Первую ладью мы можем поставить на любую из 64 клеток шахматной доски. Допустим, первая ладья заняла какую-то клетку (рис. 5). Тогда для второй ладьи годятся все клетки, кроме зачеркнутых. Следовательно, для второй ладьи остается 64-(l + 7-f 7) = 49 клеток.

Рис. 5
Умножим 64 на 49: 64 х 49 = 3136. Однако каждую расстановку на доске двух ладей мы посчитали дважды. Если, например, первая ладья стоит на d5, а вторая на 64 или если первая стоит на 64, а вторая на с/5, то это один и тот же вариант.
Следовательно, всего существует 3136 : 2 = 1568 вариантов расстановки.
Задача 41. Шестеро ребят решили покататься на трех одинаковых двухместных лодках. Сколькими способами они могут распределиться по этим лодкам?
Решение, Присвоим каждому из ребят номер от 1 до 6 и рассмотрим, как можно разбить 6 человек на три пары, (рис. 6).
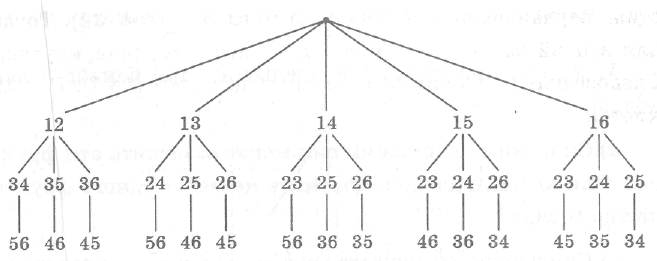
Рис. 6
Для первого существует 5 пар: 12, 13, 14, 15 и 16. Если одну лодку заняла пара 12, для остальных лодок возможны следующие пары: 34 и 56, 35 и 46, 36 и 45. Этим разбиениям соответствуют первые три ветви дерева возможных вариантов, изображенных на рис. 6. Таким образом, всего существует 15 вариантов.
