28. Сформулировать теорему о связи решений исходной и вспомогательной задач при решении задачи линейного программирования методом искусственного базиса.

S=Xn+1+…..+Xn+m к мин Вспомогательная задача всегда имеет оптимальное решение, т.к. решая симплексным методом через конечное число шагов найдем оптимальное решение т.к. 1) система совместна 2)S>=0. Если оптимальное решение дает Smin=0, тогда исходная задача либо имеет оптимальное решение, либо уходит в минус-бесконечность

29. Доказать, что если при решении задачи линейного программирования:

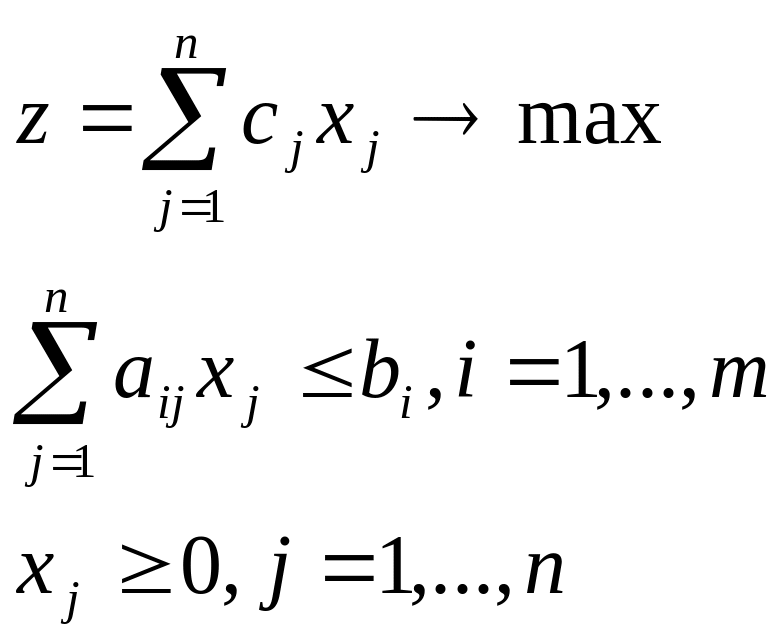
симплексным методом в качестве начального базиса выбирают базис из дополнительных переменных, для которых с_i, = 0, то оценки для всех небазисных (свободных) переменных

будут равны , а соответствующее значение целевой функции

При дополнительных переменных коэффициенты целевой функции равны 0

При базисном решении все свободные переменные равны нулю,

30. Для задачи линейного программирования:

получить выражение целевой функции z через свободные переменные общего решения системы ограничений

C₃ П₃ Н₀ Х₁ Х₂ Х₃ Х₄ Х₅ Х₆ Х₇

3 Х₂ 1

0 Х₆ 1

5 Х₃ 1

-z+1400 Двойственные оценки

Коэффициент выражения ц.ф-и через свободные переменные – это двойственные оценки (с точностью до знака)

Правило: столбец С₃ * столбец матрицы, а затем вычетается верхнее значение наверху.

Док-во: правила вычисления двойственных оценок. Без ограничений общности, базисными стали Х₁, Х₂, Х_3.

C₃ П₃ Н₀ Х₁ Х₂ Х₃ Х₄ Х₅ Х₆ Х₇

Х₁ 1 S

Х₂ 1

Х₃ 1

Двойственные оценки

F = CX= C₁X₁+ C₂X₂= C₁*X₁ + C₂*X₂= C₁(H-SX₂) + C₂( H₂) = C₁H + (-C₁S + C₂)X₂= Z₀+(-C₁S + C₂)X₂=Z₀-(C₁S- C₂)X₂=Z

Z= Z₀-(C₁S- C₂)X₂

40=X₁+ 7X₄+2X₁

H=X₁+SX₂→X₁=H-SX₂

31. Правила выбора ключевого столбца и строки при решении задачи лп симплексным методом, последствия неправильного выбора

1)Ключевой столбец выбираем по минимальной двойственной оценке

2)Потом считается столбец альфа как отношение свободного члена к коэффициенту ключевого столбца

3)По минимальной альфа выбираем ключевую строку

В качестве разрешающей неизвестной можно принять любую неизвестную, при которой есть хоть один положительный коэффициент, а затем в качества разрешающего уравнения следует взять то уравнение, которое соответствует наименьшему среди отношений свободных членов уравнений к соответствующим положительным коэффициентам при выбранной неизвестной в этих уравнениях. Условимся говорить, что СЛАУ подвергается симплексным преобразованиям, если процесс исключения неизвестных осуществляется в соответствии с указанными правилами выбора разрешающей неизвестной и разрешающего уравнения. Остается заметить, что СЛАУ не будет иметь ни одного неотрицательного решения, если в процессе симплексных преобразований в ней появится уравнение, в котором свободный член строго положителен, а среди коэффициентов при неизвестных нет ни одного положительного.