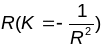- •2. Элементарная крывая. Агульныя крывыя. Простыя крывыя.
- •5. Гадкая (рэгулярная) элементарная крывая.
- •10. Датычная прамая крывой.
- •11. Нармаль плоскай крывой. Нармальная плос-касць прасторавай крывой. Вугал паміж крывымі.
- •12. Даўжыня дугі крывой. Формулы для вылічэння даўжыні дугі.
- •15. Суправаджальны трохграннік. Кананічны базіс.
- •17. Крывізна і кручэнне.
- •20. Крывізна і кручэнне акружнасці, гарфіка функцыі, шрубавай лініі.
- •21. Крывая нулявой крывізны. Пункты спрамлення (выпроствання).
- •22. Крывая нулявога кручэння. Пункты сплашчэння.
- •23. Натуральныя раўнанні. Асноўная тэарэма тэорыі крывых.
- •27. Элементарная паверхня (э.П.). Агульная павер-хня (а.П.). Простая паверхня (п.П.).
- •29. Гладкая (рэгулярная) элементарная паверхня.
- •35. Датычная плоскасць паверхні.
- •36. Нармаль паверхні. Кананічны базіс.
- •37. Першая квадратычная форма параметрызава-най паверхні. Запіс першай квадратычнай формы ва унутраных каардынатах. Дыскрымінант першай ква-дратычнай формы.
- •38. Вылічэне даўжыні дугі крывой на паверхні.
- •39. Вылічэнне вугла паміж крывымі на паверхні.
- •40. Вылічэнне плошчы абсягу на паверхні.
- •41. Другая квадратычная форма параметрызава-най паверхні.
40. Вылічэнне плошчы абсягу на паверхні.
Плошчы
абсягу D
на гладкай параметрызаванай паверхнасці
абмежаванага галдкім ці кускова гладкім
контурам і гамеаморфнага крушу наз. лік
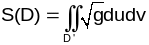 ,
дзе
,
дзе
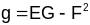 ,
а
,
а
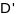 - правобраз абсягу
- правобраз абсягу
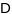 у плоскасці параметраў
.
у плоскасці параметраў
.
Заўвага
1:
Велічыня
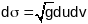 наз. элем. плошчы параметрызаванай
паверхні
наз. элем. плошчы параметрызаванай
паверхні
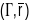
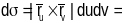
 ,
-
кіроўныя вектары каардынатных ліній
,
-
кіроўныя вектары каардынатных ліній
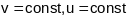 адпаведна ў
.
Т.ч.
адпаведна ў
.
Т.ч.
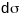 есць плошча параллелаграма, пабудаванага
на вектарах
есць плошча параллелаграма, пабудаванага
на вектарах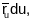
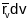 .
Гэты параллелаграм ляжыць у дачыненні
плоскасці Т да крывой
у п.
,
і яго плошча прыблізна роўна плошчы
крывалін. чатырохвугольніка на паверхні
,
абмежаванага лініямі
.
Гэты параллелаграм ляжыць у дачыненні
плоскасці Т да крывой
у п.
,
і яго плошча прыблізна роўна плошчы
крывалін. чатырохвугольніка на паверхні
,
абмежаванага лініямі


 .
Набліжэнне тым больш дакладна, чым меньш
.
.
Набліжэнне тым больш дакладна, чым меньш
.
Заўвага
2:
Азначэнне
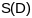 карэктна ў тым сэнсе, што інварыянтна
адносна выбару параметрызаванай
паверхні, г. зн., калі
карэктна ў тым сэнсе, што інварыянтна
адносна выбару параметрызаванай
паверхні, г. зн., калі
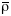 - параметр. паверхні эквів. параметрызацыі
,
тады вылічваючы
па дадзенай формуле адносна парам
атрымаем той жа вынік, што і адносна
парам
,
для абгрунтавання выкарыстоўваем
правіла замены парам. ў дваўным інтэграле.
- параметр. паверхні эквів. параметрызацыі
,
тады вылічваючы
па дадзенай формуле адносна парам
атрымаем той жа вынік, што і адносна
парам
,
для абгрунтавання выкарыстоўваем
правіла замены парам. ў дваўным інтэграле.
41. Другая квадратычная форма параметрызава-най паверхні.
Другой
квадратычнай формай гладкай
параметрызава-най паверхні
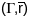 класа
класа
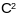 наз. выраз:
наз. выраз:
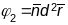 .
.
Заўвага:
форму
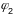 можна перапісаць па-іншаму:
можна перапісаць па-іншаму:
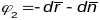 .
.
Паколькі
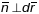 , тады
, тады
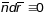 ,
дыферынцуючы будзем мець
,
дыферынцуючы будзем мець
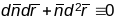 .
Адкуль маем
.
Адкуль маем
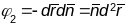 .
.
Запіс формы ва ўнутранных каардынатах.
Маем
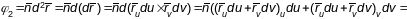
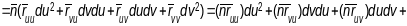
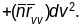
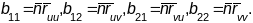
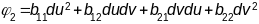
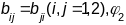 -
сіметрычная квадратычная форма адносна
*, праўда, знаканевызначаная у адрозненні
ад
-
сіметрычная квадратычная форма адносна
*, праўда, знаканевызначаная у адрозненні
ад
 .
.
Запіс формы у класічных (гаўсавых) каардынатах.
 ,
,
дзе
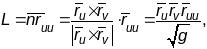
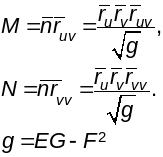
43. Нармальная крывізна паверхні. Яе геаметрычны сэнс. Кn(ﻻ)׀p=φ2/φ1=f(u,v,du,dv).
Адсюль
вынікае, што калі п.P(u,v)
фіксаваны для ўсіх крывых на паверхні
(Г,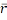 ),
якія праходзяць праз пункт Р у адным і
тым жа напрамку (du,dv),
г.зн. d
=
udu+
vdv,
іншымі словамі якія маюць адзіную
датычную прамую l
з
кіроўным вектарам d
нармальныя крывізны аднолькавыя. Гэтае
дае выснову для вывядзення велічыні,
якая характарызуе скрыўленасць самой
паверхні Г у п.Р у дадзенным напрамку.
),
якія праходзяць праз пункт Р у адным і
тым жа напрамку (du,dv),
г.зн. d
=
udu+
vdv,
іншымі словамі якія маюць адзіную
датычную прамую l
з
кіроўным вектарам d
нармальныя крывізны аднолькавыя. Гэтае
дае выснову для вывядзення велічыні,
якая характарызуе скрыўленасць самой
паверхні Г у п.Р у дадзенным напрамку.
Нармальнай крывізной паверхні Г у ея пункце Р у дадзенным напрамку наз. агульнае значэнне нармальных крывізн усіх крывых на пав-ні Г, якія праходзяць праз п.Р у гэтым напрамку. Калі пав-ня Г параметрызаваная в.-ф. гэты напрамак можна вызначыць в-рам d і абазн. kn(d ). Калі Г не параметрызаваная тады напрамак можна задаць датычнай прамой l у п.Р і абазн. kn(l). апошняе абазначэнне карэктнае таму што kn(d )=kn(-d ).

Тэарэма.
Нармальнуя крывізну kn(d
)
у
п.Р(u,v)
пав-ні (Г,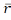 )
у напрамку d
можна вылічыць па формуле
)
у напрамку d
можна вылічыць па формуле
kn(d )׀р=φ2/φ1.
Нармальным сячэннем пав-ні Г у п.Р у напрамку яе датычнай прамой l, што праходзіць праз п.Р наз. лінія на пав-ні Г, па якой яе перасякае плоскасць, якая праходзіць праз нармаль n пав-ні Г у п.Р і прамую l.
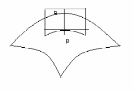
Калі вярцець датычную прамую l у датычнай плоскасці Т паверхні Г у п.Р вакол п.Р атрымаем сям’ю пав-ні у гэтым пункце.
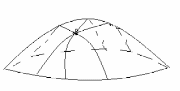
Крывізна кожнага нармальнага сячэння з гэтай сям’і характарызуе крыўленне пав-ні у п.Р у адпаведным напрамку.
Сцв. Нармальная крывізна kn(l) пав-ні Г у п.Р у напрамку l з дакладнасцю да знака роўна крывізне knc нарм. сячэння пав-ні Г, што праходзіць праз п.Р у напрамку l
kn(l)׀p=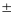 knc(l)׀p.
knc(l)׀p.
Доказ:
нармальнае сячэнне – плоская крывая,
таму орт 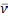 яе галоўнай нармалі калінеарны орту
яе галоўнай нармалі калінеарны орту
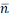 пав-ні
Г. Гэта значыць, што вугал
пав-ні
Г. Гэта значыць, што вугал 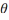 =
^
=0
ці
=π,
cos
=
1,
таму
=
^
=0
ці
=π,
cos
=
1,
таму
kn(l)= knc(l)cos = knc(l). ⊠
44.
Амбілічныя
і неамбілічныя пункты пав-ні. Галоўныя
крывізны. kn(d
)׀p=f(u,v,du,dv).
Калі Р фіксаваны пункт, тады атрымаем
ф-цыю ад 2 пераменных du,dv
(du2+dv2≠0).
Магчымы 2 выпадкі: 1)калі kn(d
)=const
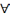 du,dv
амбілічны; 2)
kn(d
)≠const.
du,dv
амбілічны; 2)
kn(d
)≠const.
Амбілічным пунктам пав-ні наз. такі яе пункт ва ўсіх напрамках у якім нармальныя крывізны пав-ні аднолькавыя. Амбілічныя пункты могуць быць двух тыпаў. Калі у п.Р у кожным напрамку d нармальная крывізна kn(d )=0 амбілічны пункт наз. пунктам сплашчэння. Калі у амбілічным п.Р у кожным напрамку d , kn(d )=const≠0 гэты пункт наз. шаравым ці сферычным. Відавочна ўсе пункты пл-сці – амбілічныя пункты сплашчэння, усе пункты сферы – сферычныя амбілічныя пункты.
Сцв. 1) пункт сплашчэння пав-ні хар-ецца роўнасцямі L=M=N=0. 2) сферычны пункт хар-ецца дачыненнямі
 =
=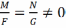 .
.
Галоўнамі крывізнамі пав-ні Г ў яе амбелічным пункце наз. найменш. і найбол. з ўсіх нармальных крывізнаў пав-ні ў гэтым пункце. У кожным неамбілічным пункце існуюць роўна дзве галоўныя крывізны.
Тэарэма. Галоўныя крывізны у неамбілічным пункце гладкай параметразаванай пав-ні класа С2 задавальняюць раўнанню
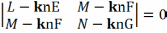
ці што тое самае
(EG-F2) kn2-(LG-2MF+NE) kn+(LN-M2)=0.
Доказ: у фіксаван. п.Р(u,v)⋴(Г, ) нармальная крывізна
kn(d )= φ2/φ1 і такім чынам прадстаўляе сабой ф-цыю двух пераменных du,dv (du2+dv2≠0) калі гэтая ф-цыя дасігае экстрымальных значэнняў адпаведна дастатковай умове экстрэмума ф-цыі двух пераменных будзем мець
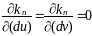 .
Таму
маем
.
Таму
маем
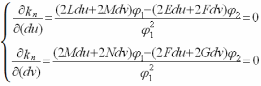
(
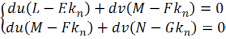
Па прадпалажэнню гэта аднароднае лінейнае адносна du,dv сістэма мае ненулявое рашэнне. Таму яе вызначальнік роўны нулю.
 .
⊠
.
⊠
Палучанае раўнанне наз. характарыстычным раўнаннем для знаходжання галоўных крывізн. У неамбілічным пункце яно мае два кораня – наім. і наіб. з нармальных крывізн у гэтым пункце, якія абазначаюцца звычайна праз k1, k2.
46. поўная (гаўсава) і сярэдняя крывізны паверхняў. Поўнай (гаўсавай) крывтзнай пав-ні Г у яе п.Р наз. здабытак k яе галоўных крывізн k1, k2 вылічаных у гэтым пункце: K= k1k2 (1)
Сярэдняй
крывізной пав-ні Г у яе пункце Р наз.
паўсума Н яе галоўных крывізнаў k1,
k2
вылічаных у гэтым пункце: Н= (k1+
k2).
(2)
(k1+
k2).
(2)
Формулы для вылічэння К і Н.
Выкарыстаем
тэарэму Віета для хар-нага раўнання
будзем мець К=
k1k2=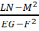
 (3)
(3)
H=
(k1+k2)=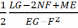
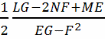 (4)
(4)
Атрымыем формулы, якія наадварот выражаюць галоўныя крывізны k1, k2 праз К і Н. запісваючы хар-нае раўнанне у выглядзе
k2
–
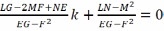
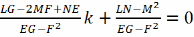
і выкарыстоўваючы ф-лы (3),(4) будзем мець k2-2Hk+K=0 (5)
Такім
чынам k1,2=H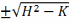 (6)
(6)
Заўвага:вмдавочна signK=sign(LN-M2). (EG-F2>0)
47. Класіфікація пунктаў рэгулярных пав-няў. Будова пав-няў у наваколлях пунктаў розных тыпаў. Пункт Р параметрызаваннай пав-ні (Г, ) наз. эліптычным калі ў ім К(Р)>0 (поўная крывізна К дадатная). Паколькі signK=sign(LN-M2) эліптычны пункт пав-ні хар-ецца няроўнасцю LN-M2>0. Улічваючы, што К= k1k2 ,атрымоўваецца, што у эліптычным пункце k1>0, k2>0 ці k1<0, k2<0, г.зн. што эліптычным пункце галоўныя нармальныя сячэнні загнуты ў адзін бок.
У наваколлі эліптычнага пункта пав-ні Г размешчана па адзін бок ад сваёй датычнай пл-сці Т і мае з ёй адзін агульны пункт – пункт дотыку.
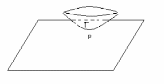
Такім чынам ў наваколлі эл. Пункта пав-ня нагадвае эліптычны парабалоід.
Гіпербалічным пунктам параметрызаванай пав-ні (Г, ) наз. такі яе пункт Р, у якім поўная крывізна К адмоўная, г.зн. К(Р)<0, ці што тое самае LN-M2<0. Галоўныя нармальныя сячэнні пав-ні у яе гіпербалічным пункце загнутыя у розныя бакі. У наваколлі гіпербал. пункта Р пав-ня Г нагадвае гіпербалічны парабалоід. Яна перасякае сваю датычную пл-сць Т у гэтым пункце па крывой для якой п.Р з’яўл. асаблівым.
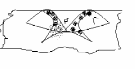
Пункт
Р наз. парабадічным калі у ім К(Р)=0  LN-M2=0
LN-M2=0
Т.ч. К= k1k2=0. Тут магчымы два выпадкі: 1. Калі ў парабалічным пункце Р k1=k2=0, тады і усе іншыя нармальныя крывізны kn=0 ці kn(P)=const=0. У гэтым выпадку Р – амбілічны пункт сплашчэння, які хар-ецца роўнасцямі L=M=N≠0. Будова пав-няў у наваколлі пункта сплашчэння можа быць разнастайнай у найпрасцейшым выпадку калі усе пункты наваколля – пункты сплашчэння яно будзе часткай пл-сці. На пав-ні можа знаходзіцца таксама ізаляваны пункт сплашчэння.
Пункты сплашчэння на пав-ні могуць утвараць і цэлыя крывыя.
2. Калі у парабалічным пункце Р ці k1=0, k2≠0 ці k1≠0, k2=0. Такі парабалічны пункт наз. уласным парабалічным і у ім LN-M2=0 і L2+M2+N2≠0.
49. Паверхні знакапераменнай, знакапастаяннай і пастаяннай поўнай крывізны. Пав-ні можна сістэматызаваць адпаведна як размяркоўваюцца на іх пункты розных тыпаў.(1) Паверхні знакапераменнай поўнай крывізны – гэта пав-ні, на якіх прысутнічаюць пункты усіх трох тыпаў: эліптычныя (k>0), гіпербалічныя (k<0), парабаліцныя (k=0). Часта часткі пав-няў, якія складаюцца з эліптычных і гіпербалічных пунктаў аддзяляюцца адна ад другой лініямі якія складаюцца з парабалічных пунктаў. Прыклад. “паверхня звон”
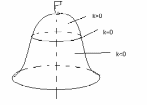
Пункт Р, які ляжыць на восі вярчэння можа быць эліптычным, сферычным ці парабалічным пунктам сплашчэння ці ў ім крывізна К можа быць не вызначана зусім.
(2) Пав-ні знакапастаяннай крывізны – гэта пав-ні, якія складаюцца цалкам ці з эліптычных пунктаў ці цалкам з гіпербалічных пунктаў. Прыклад: пав-ні знакапастаяннай крывізны 2-ога парадку. Эліптычнага тыпу: эліпсоід(сфера), двуполасцевы гіпербалоід, эліптычны парабалоід. Гіпербалічнага тыпу: аднаполасцевы гіпербалоід, гіпербалічны парабалоід.
Сцв. Поуная крывізна К у кожным пункце мінімальнай пав-ні недадатная. На самай справе ў ім
Н=0⟹ (k1+k2)⟹k2=-k1⟹К=k1k2=-k1≤0.
Найпрасцейшая мінімал. пав-ня - пл-сць ці яе частка ў кожным яе пункце К=Н=0 (k1=k2=0).
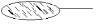
Сярод пав-няў вярчэння адзінай мінім. пав-няй з’яўл. катэноід (К<0,H=0).
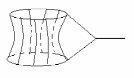
Сярод лінейчатых пав-няў (акрамя пл-сці) адзінай мінім. пав-няй з’яул. Прамы гелікоід.
(3) пав-ні пастаяннай крывізны – гэта пав-ні ўздоўж якіх К=const. яны могуць быць эліпт., гіпербаліч. І парабаліч. тыпу. Найпрасцейшымі пав-нямі пастаяннай поўнай крывізны з’яўл.: 1. Пл-сць. У кожным яе пункце К= k1k2 =0(парабалічнага тыпу).
2. Сфера радыуса R. У кожным яе пункце
К=
k1k2
=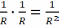 = const>0(эліптычнага
тыпу).
= const>0(эліптычнага
тыпу).
3.
Псеўдасфера радыўса R
– пав-ня вярчэння трактрысы вакол яе
асімптот. У кожным яе пункце К= .
.
Пав-ні пастаяннай поўнай крывізны нулявога парадку: эліптычны цыліндр гіпербалічны цыліндр

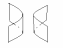
парабалічны цыліндр конус другога парадку
52. Асноўная тэарэма тэорыі паверхняў(тэарэма Банэ). Тэарэма Банэ. Няхай у аднасвязным абсяге Д пл-сці зададзены дзве квадратычныя формы
E(u,v)du2+2F(u,v)dudv+G(u,v)dv2 і
L(u,v)du2+2M(u,v)dudv+N(u,v)dv2, першая з якіх дадатна вызначаная, прычым каэфіц. E, F, G, L, M, N– непарыўна дыферыцав. Ф-цыі ў абсяге Д і звязаныя райнаннямі Гаўса і Петэрсона-Кадацы. Тады ў пр-ры існуе з дакладнасцю да руху адзіная пав-ня, для якой зададзены формы з’яўл. адпаведна першай і другой квадратычнай формамі пры некаторай яе параметрызацыі.
53. Геадэзічныя лініі. Геадэз. крывізна kg=ksinθ.(1)
Геадэзічнай
лініяй на пав-ні наз. крывая у кожным
пункце якой яе гедэзічная крывізна
роўна 0.Сцв.1.
калі на пав-ні размешчана прамая, яна
з’яўл. яе геадэз. лініяй.На самай справе,
у кожным пункце крывой, крывізна k=0,
тады kg=0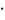 sin
=0.Заўвага.
Прамая на пав-ні з’яўл. яшчэ і асімптатычнай
лініяй. Гэта вынікае з ф-лы kn=kcosθ⟹kn=0.
З дапамогай ф-лы (1) атрымаем геаметрычны
крытэр геадэзічнай лініі.Сцв.2.
крывая на пав-ні з’яўл. геад. лініяй, т.
і т.т., калі ў кожным яе пункце, у якім
k≠0,
галоўная нармаль гэтай крывой N
супадае з нармалю n
гэтай пав-ні. На самай справе, калі k≠0,
kg=0<=>
sinθ=0<=>θ=0
ці θ=π.Г.зн.
ці
sin
=0.Заўвага.
Прамая на пав-ні з’яўл. яшчэ і асімптатычнай
лініяй. Гэта вынікае з ф-лы kn=kcosθ⟹kn=0.
З дапамогай ф-лы (1) атрымаем геаметрычны
крытэр геадэзічнай лініі.Сцв.2.
крывая на пав-ні з’яўл. геад. лініяй, т.
і т.т., калі ў кожным яе пункце, у якім
k≠0,
галоўная нармаль гэтай крывой N
супадае з нармалю n
гэтай пав-ні. На самай справе, калі k≠0,
kg=0<=>
sinθ=0<=>θ=0
ці θ=π.Г.зн.
ці  .⊠Вынік.
Вялікія акружнасці на сферы з’яўл. яе
геад. лініямі. На самай справе, вялікія
акружнасці на сферы з’яўл. плоскімі
крывымі, таму галоўная нармаль N
ляжыць на плоскасці адпаведнай акружнасці,
і праходзіць праз яе центр, але нармаль
N
сферы таксама праходзіць праз яе центр
О (
.⊠Вынік.
Вялікія акружнасці на сферы з’яўл. яе
геад. лініямі. На самай справе, вялікія
акружнасці на сферы з’яўл. плоскімі
крывымі, таму галоўная нармаль N
ляжыць на плоскасці адпаведнай акружнасці,
і праходзіць праз яе центр, але нармаль
N
сферы таксама праходзіць праз яе центр
О (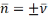 ).
У кожным ункце акружнасці N≡n.
).
У кожным ункце акружнасці N≡n.
Дыферынц.
раўнанні геадыз. Ліній ва унутраных
каардынатах. Няхай
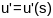 -
параметр. раунанні геадыз. крывой
на
параметрычнай пав-ні
-
параметр. раунанні геадыз. крывой
на
параметрычнай пав-ні
 класа
,
прычым
класа
,
прычым
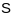 -
натуральны параметр. Патрабуем, каб у
кожным пункце крывой
орт
-
натуральны параметр. Патрабуем, каб у
кожным пункце крывой
орт
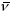 яе галоўнай нармалі
яе галоўнай нармалі
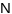 быў калінеарны орту
быў калінеарны орту
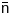 нармалі
нармалі
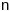 пав-ні у гэтым пункце. Для гэтага запішам
параметрычнае натуральнае раўнанне
пав-ні у гэтым пункце. Для гэтага запішам
параметрычнае натуральнае раўнанне
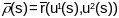 і раскладзём вектар крывізны
і раскладзём вектар крывізны
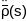 у
кожным яе пункце па кананічнаму базісу
пав-ні
у
кожным яе пункце па кананічнаму базісу
пав-ні
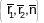 .
Па-першай ф-ле Франэ:
.
Па-першай ф-ле Франэ: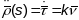 .
.
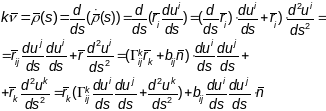
Адсюль
бачна, што
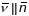 т. і т. т. калі датычныя складаемыя роўныя
0.
т. і т. т. калі датычныя складаемыя роўныя
0.
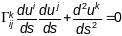 (2)
(2)
(2)
– дыферынцыяльныя раўнанні геадыз.
ліній ва ўнутраных каардынатах(нелінейная
сістэма другога парадку адносна ф-цый
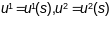 ).
У выпадку калі
).
У выпадку калі
 ,
то сістэма (2) у яўным выглядзе наступная
,
то сістэма (2) у яўным выглядзе наступная
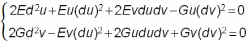 .
З тэорыі дыфер. раўнанняў вядома, калі
ф-цыі
.
З тэорыі дыфер. раўнанняў вядома, калі
ф-цыі
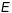 ,
,
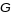 непарыўны
у абсягу Д, то гэтая сістэма мае адзінае
рашэнне пры дадзенных пачатковых умовах
непарыўны
у абсягу Д, то гэтая сістэма мае адзінае
рашэнне пры дадзенных пачатковых умовах
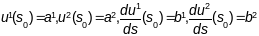 ,дзе
,дзе
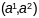 -каардынаты
адвольнага пункта абсягу Д, а
-каардынаты
адвольнага пункта абсягу Д, а
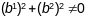 .З
геаметрычнага пункту гледжання:Тэарэма.
Праз кожны пункт гладкай пав-ні у кожным
напрамку праходзіць роўна адна геадыз.
лінія. Вынікі:1. На пл-сці геад. лініямі
з’яўл. прамые і толькі яны. 2. На сферы
геад. лініямі з’яўл. вялікія акружнасці
і толькі яны.
.З
геаметрычнага пункту гледжання:Тэарэма.
Праз кожны пункт гладкай пав-ні у кожным
напрамку праходзіць роўна адна геадыз.
лінія. Вынікі:1. На пл-сці геад. лініямі
з’яўл. прамые і толькі яны. 2. На сферы
геад. лініямі з’яўл. вялікія акружнасці
і толькі яны.
56.
Сума вуглоў геадэзічнага трохвугольніка.
Геадэзічны трохвугольнік – крывалінейны
трохвугольнік
 на гладкай пав-ні Г,бакамі якога з’яўл.
дугі
на гладкай пав-ні Г,бакамі якога з’яўл.
дугі
 геадэзічных ліній на гэтай пав-ні, і
будзем абазначаць
геадэзічных ліній на гэтай пав-ні, і
будзем абазначаць
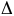 .
.
Дыфектам
геад. трохвугольніка
наз. лік
 ,дзе
,дзе
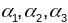 -
унутран. вуглы трохвугольнака
.Па-іншаму
гэты дыфект ёсць перавышэнне сумы вуглоў
на 1800.Сцв.1дыфект
-
унутран. вуглы трохвугольнака
.Па-іншаму
гэты дыфект ёсць перавышэнне сумы вуглоў
на 1800.Сцв.1дыфект
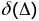 геад. трохвугольніка
супадае
з яго інтэгральнай крывізной.Па-іншаму
геад. трохвугольніка
супадае
з яго інтэгральнай крывізной.Па-іншаму
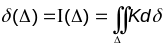 .На
самай справе выкарыстаем ф-лу
.На
самай справе выкарыстаем ф-лу
 ,
улічваючы,што тут Д=
,
,
улічваючы,што тут Д=
,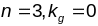 маем
маем
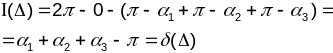 .
Вынік1.На
пав-ні эліптычнага тыпу (
.
Вынік1.На
пав-ні эліптычнага тыпу (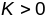 )
дыфект геад. трохвугольніка дадатны, а
сума яго вуглоў 1800.
На пав-ні гіпербалічнага тыпу(
)
дыфект геад. трохвугольніка дадатны, а
сума яго вуглоў 1800.
На пав-ні гіпербалічнага тыпу(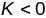 )
дыфект геадыз. трохвугольніка адмоўны,
а сума яго вуглоў менш за 1800.На
пав-ні парабалічнага тыпу
)
дыфект геадыз. трохвугольніка адмоўны,
а сума яго вуглоў менш за 1800.На
пав-ні парабалічнага тыпу
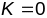 дыфект геад. трохвугольніка роўны 0, а
сума яго вуглоў роўна 1800.На
самай справе, калі, напрыклад
),
тады па сцв.1
дыфект геад. трохвугольніка роўны 0, а
сума яго вуглоў роўна 1800.На
самай справе, калі, напрыклад
),
тады па сцв.1
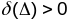 .
.

Разгледзім
трохвог.На пав-ні не нулявой пастаянай
крывізны К.Выкарыстоўвая сцв.1,атрымоўваем:
вынік2.Дыфект
геад. трохвуг.
на
пав-ні пастаянай ненулявой поўнай
крывізны К прапарцыянальны яго плошчы:
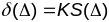 .
Вынік3.На
пав-ні пастаянай поўнай крывізны К сума
вуглоў геад. трохвугольніка
залежыць
ад яго плошчы
.
Вынік3.На
пав-ні пастаянай поўнай крывізны К сума
вуглоў геад. трохвугольніка
залежыць
ад яго плошчы
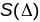 па ф-ле:
па ф-ле: Аналіз апошняй ф-лы паказвае:1.Трохвуг.
аднолькавай плошчы маюць аднолькавую
суму вуглоў,калі
Аналіз апошняй ф-лы паказвае:1.Трохвуг.
аднолькавай плошчы маюць аднолькавую
суму вуглоў,калі
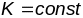 .2.Калі
.2.Калі
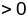 з павелічэннем
плошчы
трохвуг-каў узрастае сума яго вуглоў.3.
з павелічэннем
плошчы
трохвуг-каў узрастае сума яго вуглоў.3.
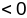 з павялічэннем плошчы трохвугольніка
памяншаецца сума яго вуглоў.
Заўвага.Улічваючы
відавочную няроўнасць
з павялічэннем плошчы трохвугольніка
памяншаецца сума яго вуглоў.
Заўвага.Улічваючы
відавочную няроўнасць
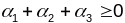 з апошняй ф-лы атрымаем
з апошняй ф-лы атрымаем
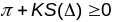 .
Адсюль, калі
.
Адсюль, калі
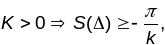
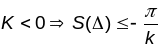 .
Апошняе паказвае, што на пав-нях пастаянай
адмоўнай крывізны не існуе трохвугол-каў
колькі вялікай плошчы, яны абавязкова
.
Апошняе паказвае, што на пав-нях пастаянай
адмоўнай крывізны не існуе трохвугол-каў
колькі вялікай плошчы, яны абавязкова
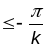 .Геад.
трохвуг-кі на мадэльных пав-нях пастаянай
крывізны пл-сці (
)
сферы радыуса
.Геад.
трохвуг-кі на мадэльных пав-нях пастаянай
крывізны пл-сці (
)
сферы радыуса
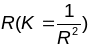 ,
паўсферы
,
паўсферы