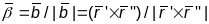- •2. Элементарная крывая. Агульныя крывыя. Простыя крывыя.
- •5. Гадкая (рэгулярная) элементарная крывая.
- •10. Датычная прамая крывой.
- •11. Нармаль плоскай крывой. Нармальная плос-касць прасторавай крывой. Вугал паміж крывымі.
- •12. Даўжыня дугі крывой. Формулы для вылічэння даўжыні дугі.
- •15. Суправаджальны трохграннік. Кананічны базіс.
- •17. Крывізна і кручэнне.
- •20. Крывізна і кручэнне акружнасці, гарфіка функцыі, шрубавай лініі.
- •21. Крывая нулявой крывізны. Пункты спрамлення (выпроствання).
- •22. Крывая нулявога кручэння. Пункты сплашчэння.
- •23. Натуральныя раўнанні. Асноўная тэарэма тэорыі крывых.
- •27. Элементарная паверхня (э.П.). Агульная павер-хня (а.П.). Простая паверхня (п.П.).
- •29. Гладкая (рэгулярная) элементарная паверхня.
- •35. Датычная плоскасць паверхні.
- •36. Нармаль паверхні. Кананічны базіс.
- •37. Першая квадратычная форма параметрызава-най паверхні. Запіс першай квадратычнай формы ва унутраных каардынатах. Дыскрымінант першай ква-дратычнай формы.
- •38. Вылічэне даўжыні дугі крывой на паверхні.
- •39. Вылічэнне вугла паміж крывымі на паверхні.
- •40. Вылічэнне плошчы абсягу на паверхні.
- •41. Другая квадратычная форма параметрызава-най паверхні.
11. Нармаль плоскай крывой. Нармальная плос-касць прасторавай крывой. Вугал паміж крывымі.
Нармаллю крывой у яе пункце называецца прамая, якая праходзіць праз гэты пункт, перпендыкулярна датычнай прамой да гэтай крывой у гэтым пункце. Абазначаецца праз N.
Сцверджанне1: Усякая гладкая плоска крывая ў кожным сваім пункце мае адзіную нармаль. Кіроўны вектар ёсць нармальны вектар датычнай прамой у пункце P.
Сцверджанне2:
Калі плоская крывая
 зададзена неяўна
зададзена неяўна
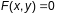 і пры гэтым
і пры гэтым
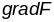 непарыўны і адрозніваецца ад
непарыўны і адрозніваецца ад
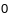 у яе пункце, тады вектар
у яе пункце, тады вектар
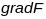 з’яўляецца кіроўным вектарам нармалі
ці, што таксама нармальным вектарам
датычнай прамой да крывой у пункце
з’яўляецца кіроўным вектарам нармалі
ці, што таксама нармальным вектарам
датычнай прамой да крывой у пункце
 .
.
Доказ:
Выбярэм некаторую параметрызацыю крывой
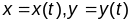 .
Тады ўздоўж
будзем мець тоеснасць
.
Тады ўздоўж
будзем мець тоеснасць
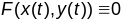 .
Дыфферэнцыруя па
.
Дыфферэнцыруя па
 гэтая роўнасць
гэтая роўнасць
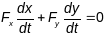 ,
,
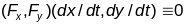 ,
,
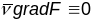 ,
,
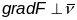 .
.
Нармальная плоскасць прасторавай крывой у пункце – плоскасць, якая проходзіць праз гэты пункт і перпендыкулянры датычнай прамой да крывой праведзенай у гэтым пункце.
Сцверджанне1:
Калі прасторавая крывая
зададзеная няяўнымі раўнаннямі
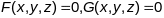
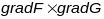 ,
прычым вектар
,
прычым вектар
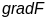 ,
,
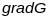 і арозніваюцца ад
уздоўж
,
тады
і арозніваюцца ад
уздоўж
,
тады
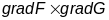 будзе нармальным вектарам нармальнай
плоскасці
будзе нармальным вектарам нармальнай
плоскасці
 ці кіроўны вектар датычнай прамой Т у
адпаведным пункце
ці кіроўны вектар датычнай прамой Т у
адпаведным пункце
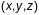 .
.
Вугал
паміж крывымі
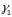 і
і
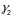 у пункце іх перасячэнная Р называецца
любы з двух змежных вуглой
у пункце іх перасячэнная Р называецца
любы з двух змежных вуглой
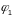 ці
ці
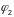
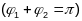 паміж іх датычнымі прамымі Т1
і Т2
адпаведна праведзены у пункце Р. Гэты
вугал можна знайсці па формуле
паміж іх датычнымі прамымі Т1
і Т2
адпаведна праведзены у пункце Р. Гэты
вугал можна знайсці па формуле
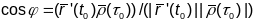 ,
дзе
,
дзе
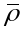 - параметрызацыя
,
- параметрызацыя
- параметрызацыя
,
- параметрызацыя
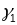 ,
,
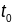 ,
,
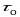 - параметры . Нармальнай плоскасцю
прасторавай крывой
у яе пункце Р наз. плоскасць, якая
праходзіць праз пункт Р артаганальна
датычнай прамой Т крывой
у гэтым пункце. У пункце Р можна правесці
бясконцую колькасць нармалей да
прасторавай крывой
,
усе яны ляжаць у нармальнай плоскасці
.
- параметры . Нармальнай плоскасцю
прасторавай крывой
у яе пункце Р наз. плоскасць, якая
праходзіць праз пункт Р артаганальна
датычнай прамой Т крывой
у гэтым пункце. У пункце Р можна правесці
бясконцую колькасць нармалей да
прасторавай крывой
,
усе яны ляжаць у нармальнай плоскасці
.
12. Даўжыня дугі крывой. Формулы для вылічэння даўжыні дугі.
Даўжыней
дугі А1А2
гладкай крывой
называецца лік
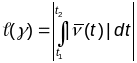 ,
,
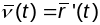 ,
дзе
,
дзе
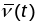 - адвольная дапушчальная параметрызацыя,
- адвольная дапушчальная параметрызацыя,
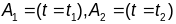 .
.
Заўвага:
Азначэнне карэктна ў тым сэнсе, што не
залежыць ад выбару дапушчальнага
параметра. На самой справе
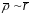 ,
гэта значыць
,
гэта значыць
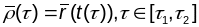 .
Дыфферэнцыруя па
.
Дыфферэнцыруя па
 будзем мець
будзем мець
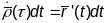 ,
,
 ,
,
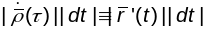 ,
,
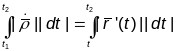 ,
,
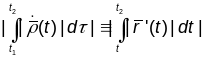 .
.
Спецыяльныя формулы для вылічэння даўжыні дугі:
(1)
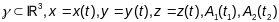 ,
,
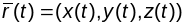
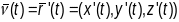
 (1).
(1).
(2)
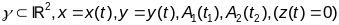
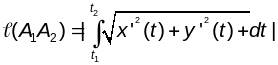 (2).
(2).
(3)
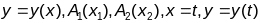 . Выкарыстоўваючы папярэднюю формулу
будзем мець
. Выкарыстоўваючы папярэднюю формулу
будзем мець
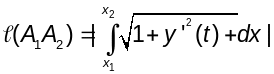 (3).
(3).
15. Суправаджальны трохграннік. Кананічны базіс.
Няхай
- бірэгулярная прасторавая крывая,
 , Т – датычная,
, Т – датычная,
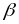 - нармальная плоскасць, якія праходзяць
праз пункт Р. праз пункт Р праходзіць
бясконцае мноства нармаляў крывой
,
якія ляжаць у плоскасці
- нармальная плоскасць, якія праходзяць
праз пункт Р. праз пункт Р праходзіць
бясконцае мноства нармаляў крывой
,
якія ляжаць у плоскасці
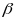 .
Выдзелім з іх дзве асобныя: нармаль,
якая праходзіць у сутыкальнай плоскасці
.
Выдзелім з іх дзве асобныя: нармаль,
якая праходзіць у сутыкальнай плоскасці
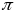 называецца асобнай. Абазначаецца
N.
Нармаль препендыкулярна сутыкальнай
плоскасці
называецца асобнай. Абазначаецца
N.
Нармаль препендыкулярна сутыкальнай
плоскасці
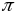 называецца бінармальнай. Абазначаецца
B.
Плоскасць,
якая праходзіць праз датычную прамую
Т і бінармальн В называецца выпрастоўнай
(спрямляющей).
называецца бінармальнай. Абазначаецца
B.
Плоскасць,
якая праходзіць праз датычную прамую
Т і бінармальн В называецца выпрастоўнай
(спрямляющей).
Суправаджальным
трохграннікам прасторовай крывой
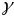 у яе пункце Р называецца трохгранны
вугал з вяршынай ў пункце Р і промымі
плоскімі вугламі пры ім, канты якога
ляжаць на датычнай Т, а грані ў сутыкальнай
плоскасці
,
нармаль плоскасці
у яе пункце Р называецца трохгранны
вугал з вяршынай ў пункце Р і промымі
плоскімі вугламі пры ім, канты якога
ляжаць на датычнай Т, а грані ў сутыкальнай
плоскасці
,
нармаль плоскасці
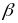 і выпрастоўнай плоскасці
і выпрастоўнай плоскасці
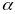 .
.
Сцверджанне: кожная бірэгулярная крывая ў кожным сваім пукце мае суправаджальны трохграннік і пры тым толькі адзін.
Правая
тройка вектароў
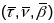 ,
дзе
,
дзе
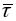 – орт датычнай Т,
– орт датычнай Т,
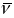 - орт галоўнай нармалі N,
- орт галоўнай нармалі N,
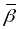 - орт бінармалі В, называецца кананічным
базісам крывой
(у пункце Р).
- орт бінармалі В, называецца кананічным
базісам крывой
(у пункце Р).
Чацверка
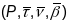 ,
дзе
,
дзе
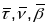 адкладзены ад пункта Р крывой
называецца кананічным рэперам. Ведаючы
кананічны рэпер легка знайсці ўсе
элементы суправаджальнага трохгранніка.
адкладзены ад пункта Р крывой
называецца кананічным рэперам. Ведаючы
кананічны рэпер легка знайсці ўсе
элементы суправаджальнага трохгранніка.
Існуюць
залежнасці:
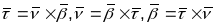 .
.
Узнікае
пытанне: як знайсці вектары
 ведаючы параметрызацыю крывой
.
Магчымы два выпадкі:
ведаючы параметрызацыю крывой
.
Магчымы два выпадкі:
1.
Крывая
зададзена натуральнай параметрызацыяй
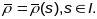
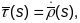
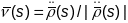 ,
,
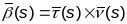 .
.
Першая
формула вынікае з таго, што
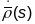 кіроўны вектар датычнай прамой Т, і
акрамя таго
кіроўны вектар датычнай прамой Т, і
акрамя таго
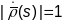 ,
паколькі
,
паколькі
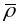 - натуральная параметрызацыя. Другая
формула выконваецца таму, што па-першае
- натуральная параметрызацыя. Другая
формула выконваецца таму, што па-першае
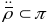 ,
па-другое
,
па-другое
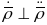 (паколькі
(паколькі
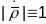

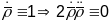
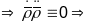 ).
).
2.
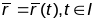 – заданне крывой
,
наступныя вектары з’яўляюцца, відавочна,
кіроўнымі вектарамі Т, В, N
адпаведна:
– заданне крывой
,
наступныя вектары з’яўляюцца, відавочна,
кіроўнымі вектарамі Т, В, N
адпаведна:

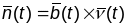 ,
,
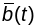 - кіроўны вектар бінармалі В,
- кіроўны вектар бінармалі В,
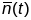 - кіроўны вектар галоўнай нармалі N
у пункце Р(t)
(з параметрам t).
Нармуючы гэтыя вектары знойдзем вектары
кананічнага базісу у кожным адпаведным
пункце:
- кіроўны вектар галоўнай нармалі N
у пункце Р(t)
(з параметрам t).
Нармуючы гэтыя вектары знойдзем вектары
кананічнага базісу у кожным адпаведным
пункце:
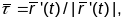
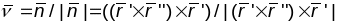 ,
,